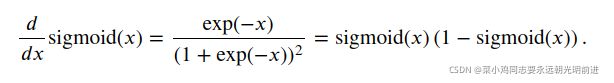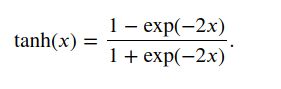深度学习常见的激活函数

ReLU函数

        ReLU提供了一种非常简单的非线性变换]。 给定元素x，ReLU函数被定义为该元素与00的最大值

        

        ReLU函数通过将相应的激活值设为0来仅保留正元素并丢弃所有负元素 ，为了直观感受一下，我们可以画出函数的曲线图。正如从图中所看到，激活函数是分段线性的    

x = torch.arange(-8.0, 8.0, 0.1, requires_grad=True)
y = torch.relu(x)
d2l.plot(x.detach(), y.detach(), 'x', 'relu(x)', figsize=(5, 2.5))

        当输入为负时，ReLU函数的导数为0，而当输入为正时，ReLU函数的导数为1。注意，当输入值精确等于0时，ReLU函数不可导。我们可以忽略这种情况，因为输入可能永远都不会是0。

        使用ReLU的原因是，它求导表现得特别好：要么让参数消失，要么让参数通过。这使得优化表现得更好，并且ReLU减轻了困扰以往神经网络的梯度消失问题

        注意，ReLU函数有许多变体，包括参数化ReLU，该变体为ReLU添加了一个线性项，因此即使参数是负的，某些信息仍然可以通过：

       

sigmoid函数 

        对于一个定义域在ℝR中的输入，sigmoid函数将输入变换为区间(0, 1)上的输出

        

        下面，我们绘制sigmoid函数。注意，当输入接近0时，sigmoid函数接近线性变换

y = torch.sigmoid(x)
d2l.plot(x.detach(), y.detach(), 'x', 'sigmoid(x)', figsize=(5, 2.5))

        sigmoid函数的导数为下面的公式：

        

        

# 清除以前的梯度。
x.grad.data.zero_()
y.backward(torch.ones_like(x),retain_graph=True)
d2l.plot(x.detach(), x.grad, 'x', 'grad of sigmoid', figsize=(5, 2.5))

 tanh函数

        与sigmoid函数类似，[tanh(双曲正切)函数也能将其输入压缩转换到区间(-1, 1)

        

y = torch.tanh(x)
d2l.plot(x.detach(), y.detach(), 'x', 'tanh(x)', figsize=(5, 2.5))

# 清除以前的梯度。
x.grad.data.zero_()
y.backward(torch.ones_like(x),retain_graph=True)
d2l.plot(x.detach(), x.grad, 'x', 'grad of tanh', figsize=(5, 2.5))

小结

• 多层感知机在输出层和输入层之间增加一个或多个全连接的隐藏层，并通过激活函数转换隐藏层的输出。
• 常用的激活函数包括ReLU函数、sigmoid函数和tanh函数。