共轭梯度法(Conjugate Gradients)(2)
最近在看ATOM,作者在线训练了一个分类器,用的方法是高斯牛顿法和共轭梯度法。看不懂,于是恶补了一波。学习这些东西并不难,只是难找到学习资料。简单地搜索了一下,许多文章都是一堆公式,这谁看得懂啊。
后来找到一篇《An Introduction to the Conjugate Gradient Method Without the Agonizing Pain》,解惑了。
为什么中文没有这么良心的资料呢?英文看着费劲,于是翻译过来搬到自己的博客,以便回顾。
由于原文比较长,一共 66 66 66 页的PDF,所以这里分成几个部分来写。
目录
共轭梯度法(Conjugate Gradients)(1)
共轭梯度法(Conjugate Gradients)(2)
共轭梯度法(Conjugate Gradients)(3)
共轭梯度法(Conjugate Gradients)(4)
共轭梯度法(Conjugate Gradients)(5)
6. Convergence Analysis of Steepest Descent
(最陡下降的收敛性分析)
6.1 Instant Results(实例结果)
为了理解最速下降的收敛性,先考虑这一种情况:
e ( i ) e_{(i)} e(i) 是一个特征向量 ,特征值是 λ e \lambda_{e} λe
于是,残差 r ( i ) r_{(i)} r(i) 也是是一个特征向量, r ( i ) = − A e ( i ) = − λ e e ( i ) r_{(i)} = - A e_{(i)}=-\lambda_e e_{(i)} r(i)=−Ae(i)=−λee(i)
由误差的定义: e ( i ) = x ( i ) − x e_{(i)} = x_{(i)} - x e(i)=x(i)−x ,以及 公式(12): x ( i + 1 ) = x ( i ) + α ( i ) r ( i ) x_{(i+1)} = x_{(i)} + \alpha_{(i)}r_{(i)} x(i+1)=x(i)+α(i)r(i),有:
e ( i + 1 ) = e ( i ) + r ( i ) T r ( i ) r ( i ) T A r ( i ) r ( i ) = e ( i ) + r ( i ) T r ( i ) λ e r ( i ) T r ( i ) ( − λ e e ( i ) ) = 0 \begin{aligned} e_{(i+1)} & = e_{(i)} + \dfrac{r^T_{(i)} r_{(i)} }{ r^T_{(i)} A r_{(i)} } r_{(i)} \\[1.5em] &= e_{(i)} + \dfrac{r^T_{(i)} r_{(i)} }{ \lambda_e r^T_{(i)} r_{(i)} }(-\lambda_e e_{(i)}) \\[1.5em] &= 0 \end{aligned} e(i+1)=e(i)+r(i)TAr(i)r(i)Tr(i)r(i)=e(i)+λer(i)Tr(i)r(i)Tr(i)(−λee(i))=0
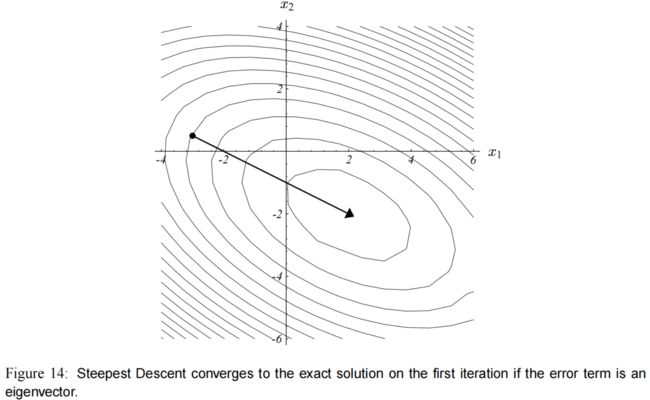
图(14) 展示了为什么走一步就能收敛到精确解。
点 x ( i ) x_{(i)} x(i) 处于椭圆的其中一个轴上,而残差直接指向椭圆的中心,令 α ( i ) = λ e − 1 \alpha_{(i)} = \lambda_e^{-1} α(i)=λe−1 可以立刻收敛。
对于更一般的分析,我们需要把 e ( i ) e_{(i)} e(i) 表示为特征向量的线性组合,并且,要进一步地要求它们是正交的。
我们知道,如果 A A A 是对称的,则它存在 n n n 个正交的特征向量。(证明见附录C2)
又由于我们可以任意缩放特征向量,因此这里我们选择的特征向量具有单位长度。
于是得到以下有用的性质:
v j T v k = { 1 , j = k , 0 , j ≠ k . (17) v_j^T v_k = \left\{ \begin{aligned} 1, & \qquad j=k, \\ 0, & \qquad j \neq k. \end{aligned} \right. \tag{17} vjTvk={1,0,j=k,j=k.(17)
把误差项表示为特征向量的线性组合: e ( i ) = ∑ j = 1 n ξ j v j (18) e_{(i)} = \sum^n_{j=1} \xi_j v_j \tag{18} e(i)=j=1∑nξjvj(18)
其中 ξ j \xi_j ξj 是 e ( i ) e_{(i)} e(i) 的第 j j j 个特征向量的长度。
由 公式(17) 和 公式(18),有如下定义:
r ( i ) = − A e ( i ) = − ∑ j ξ j λ j v j (19) r_{(i)} = -A e_{(i)} = - \sum_j \xi_j \lambda_j v_j \tag{19} r(i)=−Ae(i)=−j∑ξjλjvj(19) ∥ e ( i ) ∥ 2 = e ( i ) T e ( i ) = ∑ j ξ j 2 (20) \| e_{(i)} \|^2 = e^T_{(i)} e_{(i)} =\sum_j \xi_j^2 \tag{20} ∥e(i)∥2=e(i)Te(i)=j∑ξj2(20) e ( i ) T A e ( i ) = ( ∑ j ξ j v j T ) ( ∑ j ξ j λ j v j ) = ∑ j ξ j 2 λ j (21) e^T_{(i)} A e_{(i)} = ( \sum_j \xi_j v_j^T ) (\sum_j \xi_j \lambda_j v_j) = \sum_j \xi^2_j \lambda_j \tag{21} e(i)TAe(i)=(j∑ξjvjT)(j∑ξjλjvj)=j∑ξj2λj(21) ∥ r ( i ) ∥ 2 = r ( i ) T r ( i ) = ∑ j ξ j 2 λ j 2 (22) \| r_{(i)} \|^2 = r^T_{(i)} r_{(i)} =\sum_j \xi_j^2 \lambda_j^2\tag{22} ∥r(i)∥2=r(i)Tr(i)=j∑ξj2λj2(22) r ( i ) T A r ( i ) = ∑ j ξ j 2 λ j 3 (23) r^T_{(i)} A r_{(i)} =\sum_j \xi_j^2 \lambda_j^3\tag{23} r(i)TAr(i)=j∑ξj2λj3(23)
式子(19) 表明, r ( i ) r_{(i)} r(i) 也能表示为特征向量的和。每个特征向量的长度为 − ξ j λ j -\xi_j \lambda_j −ξjλj。
式子(20) 和 式子(22) 是毕达哥拉斯法则(Pythagoras’ Law)。
下面继续进行分析,由 公式(12) 有:
e ( i + 1 ) = e ( i ) + r ( i ) T r ( i ) r ( i ) T A r ( i ) r ( i ) = e ( i ) + ∑ j ξ j 2 λ j 2 ∑ j ξ j 2 λ j 3 r ( i ) (24) \begin{aligned} e_{(i+1)} & = e_{(i)} + \dfrac{r^T_{(i)} r_{(i)} }{ r^T_{(i)} A r_{(i)} } r_{(i)} \\[1.5em] &= e_{(i)} + \dfrac{ \sum_j \xi_j^2 \lambda_j^2 }{ \sum_j \xi_j^2 \lambda_j^3 } r_{(i)} \tag{24} \end{aligned} e(i+1)=e(i)+r(i)TAr(i)r(i)Tr(i)r(i)=e(i)+∑jξj2λj3∑jξj2λj2r(i)(24)
我们在6.1节开头的例子里看到。如果 e ( i ) e_{(i)} e(i) 仅由 1 1 1 个特征向量组成,那只要选 α ( i ) = λ e − 1 \alpha_{(i)} = \lambda_e^{-1} α(i)=λe−1,一次就能收敛。
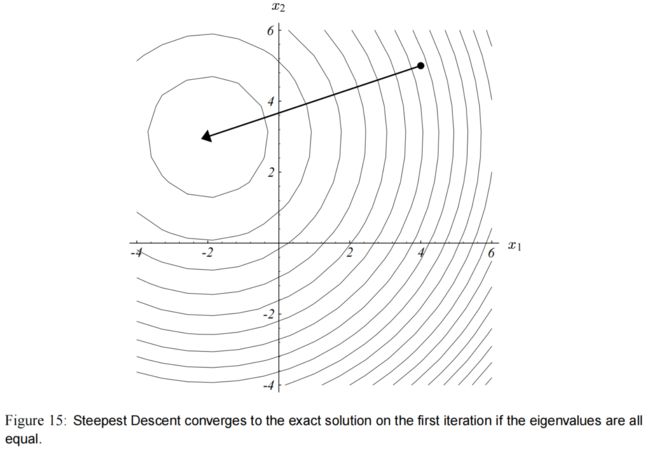
现在假定 e ( i ) e_{(i)} e(i) 是任意的,但所有特征向量的特征值都是 λ \lambda λ,则 公式(24) 变成: e ( i + 1 ) = e ( i ) + λ 2 ∑ j ξ j 2 λ 3 ∑ j ξ j 2 ( − λ e ( i ) ) = 0 (24) \begin{aligned} e_{(i+1)} & = e_{(i)} + \dfrac{ \lambda^2 \sum_j \xi_j^2 }{ \lambda^3 \sum_j \xi_j^2 } {\large(} -\lambda e_{(i)} {\large)} \\[1.5em] &= 0 \tag{24} \end{aligned} e(i+1)=e(i)+λ3∑jξj2λ2∑jξj2(−λe(i))=0(24)
图(15) 再次展示了为什么可以立即收敛。因为所有特征值都相等,那椭圆就变成了圆形,因此,无论从哪一点开始,残差必定指向圆心。和之前一样,设置 α ( i ) = λ − 1 \alpha_{(i)} = \lambda^{-1} α(i)=λ−1。
然而,如果几个特征值是不相等的、非零的,那就无法选择合适的 α ( i ) \alpha_{(i)} α(i) 来把每一个特征向量都抵消掉,我们的选择就变成了一种妥协。
实际上, 公式(24) 里的分数部分 最好是被看做 特征值 λ j − 1 \lambda_j^{-1} λj−1 的加权平均。权重 ξ j 2 \xi_j^2 ξj2 保证了 e ( i ) e_{(i)} e(i) 中较长的成分(那个特征向量)优先级低。结果就是,在某一次迭代中, e ( i ) e_{(i)} e(i) 中较短的成分(特征向量)可能会增加长度(较长的从来不会被考虑)。因此,最陡下降和共轭梯度被称为粗糙的(roughers)。相比之下,雅克比方法是平滑的(smoother)。最速下降和共轭梯度不是平滑的,尽管大多数数学教材认为平滑。
6.2 General Convergence(一般收敛性)
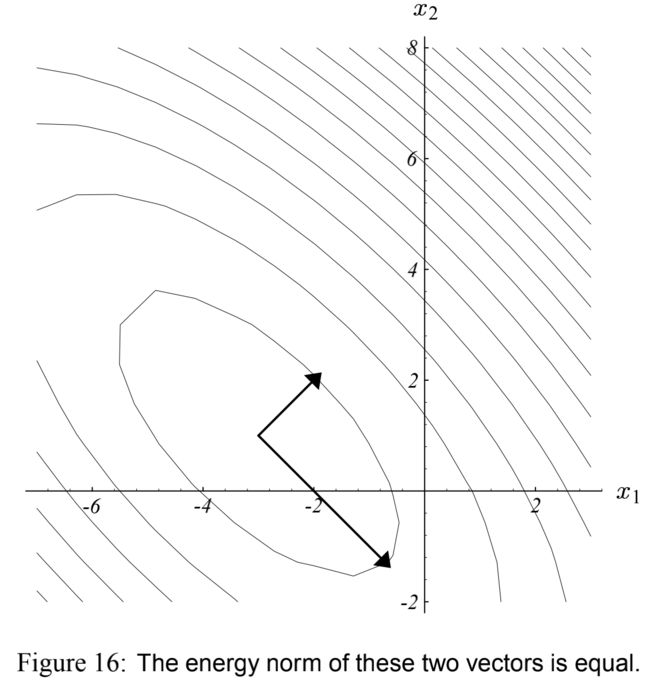
为了约束最速下降在一般情况下的收敛性,我们定义能量范数(energy norm) ∥ e ∥ A = ( e T A e ) 1 / 2 \|e\|_A = (e^T A e)^{1/2} ∥e∥A=(eTAe)1/2
如 图(16) 所示
这个范数比欧几里得范数(Euclidean norm)更好用,某种情况下更自然。公式(8) 表明最小化 ∥ e ( i ) ∥ A \| e_{(i)}\|_A ∥e(i)∥A 和最小化 f ( x ( i ) ) f(x_{(i)}) f(x(i)) 是等价的。对于这个范数我们有:
∥ e ( i + 1 ) ∥ A 2 = e ( i + 1 ) T A e ( i + 1 ) = ( e ( i ) T + α ( i ) r ( i ) T ) A ( e ( i ) + α ( i ) r ( i ) ) (by Equation 12) = e ( i ) T A e ( i ) + 2 α ( i ) r ( i ) T A e ( i ) + α ( i ) 2 r ( i ) T A r ( i ) (by symmetry of A) = ∥ e ( i ) ∥ A 2 + 2 r ( i ) T r ( i ) r ( i ) T A r ( i ) ( − r ( i ) T r ( i ) ) + ( r ( i ) T r ( i ) r ( i ) T A r ( i ) ) 2 r ( i ) T A r ( i ) = ∥ e ( i ) ∥ A 2 − ( r ( i ) T r ( i ) ) 2 r ( i ) T A r ( i ) = ∥ e ( i ) ∥ A 2 ( 1 − ( r ( i ) T r ( i ) ) 2 ( r ( i ) T A r ( i ) ) ( e ( i ) T A e ( i ) ) ) = ∥ e ( i ) ∥ A 2 ( 1 − ( ∑ j ξ j 2 λ j 2 ) 2 ( ∑ j ξ j 2 λ j 3 ) ( ∑ j ξ j 2 λ j ) ) (by Identities 21, 22, 23) = ∥ e ( i ) ∥ A 2 ω 2 , ω 2 = 1 − ( ∑ j ξ j 2 λ j 2 ) 2 ( ∑ j ξ j 2 λ j 3 ) ( ∑ j ξ j 2 λ j ) (25) \begin{aligned} \| e_{(i+1)}\|^2_A &= e_{(i+1)}^T A e_{(i+1)} \\[0.5em] &= ( e_{(i)}^T + \alpha_{(i)}r_{(i)}^T ) A ( e_{(i)} + \alpha_{(i)}r_{(i)} ) \qquad \text{(by Equation 12)} \\[0.5em] &= e_{(i)}^T A e_{(i)} + 2\alpha_{(i)} r_{(i)}^T A e_{(i)} + \alpha_{(i)}^2 r_{(i)}^T A r_{(i)} \qquad \text{(by symmetry of A)} \\[0.5em] &= \| e_{(i)}\|^2_A + 2 \dfrac{r^T_{(i)} r_{(i)} }{ r^T_{(i)} A r_{(i)} } \left( - r_{(i)}^T r_{(i)} \right) + \left( \dfrac{r^T_{(i)} r_{(i)} }{ r^T_{(i)} A r_{(i)} } \right)^2 r^T_{(i)} A r_{(i)} \\[1.5em] &= \| e_{(i)}\|^2_A - \dfrac{ ( r^T_{(i)} r_{(i)} )^2 }{ r^T_{(i)} A r_{(i)} } \\[1.5em] &= \| e_{(i)}\|^2_A \left( 1- \dfrac{ ( r^T_{(i)} r_{(i)} )^2 }{ (r^T_{(i)} A r_{(i)} )(e^T_{(i)} A e_{(i)} ) } \right) \\[1.5em] &= \| e_{(i)}\|^2_A \left( 1- \dfrac{ ( \sum_j \xi_j^2 \lambda_j^2)^2 }{ ( \sum_j \xi_j^2 \lambda_j^3)( \sum_j \xi_j^2 \lambda_j) } \right) \qquad \text{(by Identities 21, 22, 23)} \\[1.5em] &= \| e_{(i)}\|^2_A \omega^2, \qquad \omega^2= 1- \dfrac{ ( \sum_j \xi_j^2 \lambda_j^2)^2 }{ ( \sum_j \xi_j^2 \lambda_j^3)( \sum_j \xi_j^2 \lambda_j) } \end{aligned} \tag{25} ∥e(i+1)∥A2=e(i+1)TAe(i+1)=(e(i)T+α(i)r(i)T)A(e(i)+α(i)r(i))(by Equation 12)=e(i)TAe(i)+2α(i)r(i)TAe(i)+α(i)2r(i)TAr(i)(by symmetry of A)=∥e(i)∥A2+2r(i)TAr(i)r(i)Tr(i)(−r(i)Tr(i))+(r(i)TAr(i)r(i)Tr(i))2r(i)TAr(i)=∥e(i)∥A2−r(i)TAr(i)(r(i)Tr(i))2=∥e(i)∥A2(1−(r(i)TAr(i))(e(i)TAe(i))(r(i)Tr(i))2)=∥e(i)∥A2(1−(∑jξj2λj3)(∑jξj2λj)(∑jξj2λj2)2)(by Identities 21, 22, 23)=∥e(i)∥A2ω2,ω2=1−(∑jξj2λj3)(∑jξj2λj)(∑jξj2λj2)2(25)
这个分析依赖于找到 ω \omega ω 的一个上界。为了说明权值和特征值是如何影响收敛性的,我来推导一个 n = 2 n=2 n=2 时的结果。(就是有 2 2 2个特征向量)。
假设 λ 1 > λ 2 \lambda_1 > \lambda_2 λ1>λ2, A A A 的光谱条件数(spectral condition number) 定义为 κ = λ 1 λ 2 ≥ 1 \kappa= \dfrac{\lambda_1}{\lambda_2} \geq 1 κ=λ2λ1≥1。
e ( i ) e_{(i)} e(i) 的斜坡(slope)(它与“由特征向量定义的坐标系统”相关)依赖于起始点。斜坡用 μ = ξ 2 ξ 1 \mu = \dfrac{\xi_2}{\xi_1} μ=ξ1ξ2 表示。
我们有: ω 2 = 1 − ( ξ 1 2 λ 1 2 + ξ 2 2 λ 2 2 ) 2 ( ξ 1 2 λ 1 + ξ 2 2 λ 2 ) ( ξ 1 2 λ 1 3 + ξ 2 2 λ 2 3 ) = 1 − ( κ 2 + μ 2 ) 2 ( κ + μ 2 ) ( κ 3 + μ 2 ) (26) \begin{aligned} \omega^2 &= 1 - \dfrac{ (\xi_1^2 \lambda_1^2 + \xi_2^2 \lambda_2^2)^2 }{ (\xi_1^2 \lambda_1 + \xi_2^2\lambda_2) (\xi_1^2\lambda_1^3+ \xi_2^2\lambda_2^3) } \\[1.5em] &= 1- \dfrac{ (\kappa^2 + \mu^2)^2}{ (\kappa + \mu^2) (\kappa^3+\mu^2)} \tag{26} \end{aligned} ω2=1−(ξ12λ1+ξ22λ2)(ξ12λ13+ξ22λ23)(ξ12λ12+ξ22λ22)2=1−(κ+μ2)(κ3+μ2)(κ2+μ2)2(26)
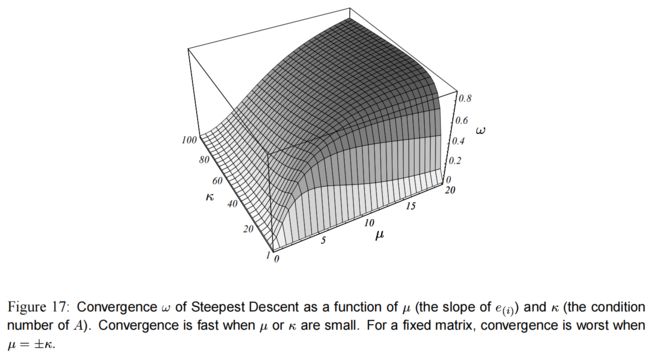
ω \omega ω 的值决定了最陡下降的收敛速度,图(17) 展示的是它关于 μ \mu μ 和 κ \kappa κ 的函数。
这张图和我的两个例子相符合。
∙ \bullet ∙ 如果 e ( 0 ) e_{(0)} e(0) 是一个特征向量,然后斜坡 μ \mu μ 是 0 0 0(或者无穷);可已从图中看到,这时 ω \omega ω 为 0 0 0,可以立即收敛。
∙ \bullet ∙ 如果特征值都相等,则条件数(condition number) κ \kappa κ 为 1 1 1,于是 ω \omega ω 也是 0 0 0。
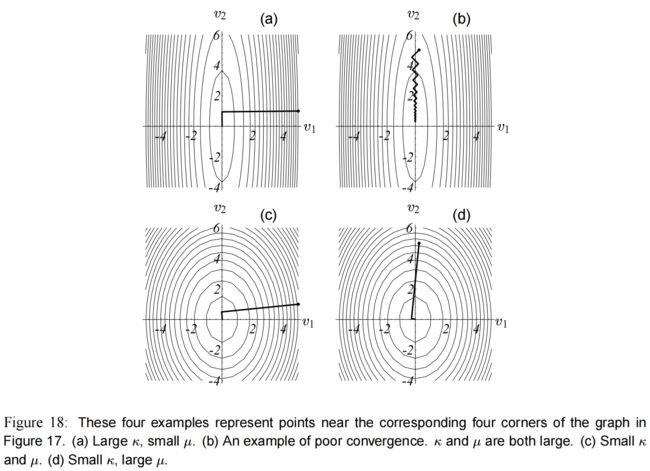
如果处于 图(17) 的 4 4 4 个角落附近,那收敛情况就如 图(18) 所示。
这些二次型的坐标系统由它们的特征向量决定,都画在 图(18) 上了。
图(18)a 和 图(18)b 是条件数较大的情况。
如果你幸运地在 图(18)a 那里开始( κ \kappa κ 大, μ \mu μ 小),那最陡下降可以很快收敛。
然而,当 κ \kappa κ 很大的时候,通常你会出现在比较糟糕的地方( μ \mu μ 也很大),见 图(18)b 。
解释一下:从 图(12) 可以看到,特征值越大的那个方向,越陡峭,梯度越大。
所以 图(18)a 和 图(18)b 两张中, v 1 v_1 v1 的特征值都是大于 v 2 v_2 v2,即 λ 1 \lambda_1 λ1 > λ 2 \lambda_2 λ2,所以 κ \kappa κ 大。
μ \mu μ 方面:
图(18)a 中 v 1 v1 v1 的长度大于 v 2 v_2 v2,即 ξ 1 \xi_1 ξ1 > ξ 2 \xi_2 ξ2,所以 μ \mu μ 小。
图(18)b 中 v 1 v1 v1 的长度小于 v 2 v_2 v2,即 ξ 1 \xi_1 ξ1 < ξ 2 \xi_2 ξ2,所以 μ \mu μ 大。
图(18)c 和 图(18)d 中, κ \kappa κ 相对较小(俩特征值差不多),所以二次型接近圆形,无论起点在哪里都能快速收敛。
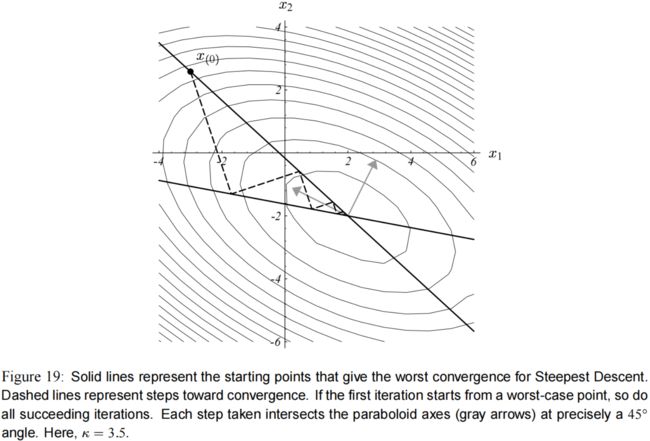
由于 A A A 是固定的,那 κ \kappa κ 就是常量,经过简单的推导可知,当 μ = ± κ \mu = \pm \kappa μ=±κ 时,使得 式子(26) 最大。
在 图(17) 中你可以看到一条微弱的山脊,那就是 μ = ± κ \mu = \pm \kappa μ=±κ 时的情况。
对于本教程的例子里的 A A A,如果选择了一个最糟糕的起点,那就如 图(19) 所示。这样的起点不止一个,这条直线上都是: ξ 2 ξ 1 = ± κ \dfrac{\xi_2}{\xi_1} = \pm \kappa ξ1ξ2=±κ 。
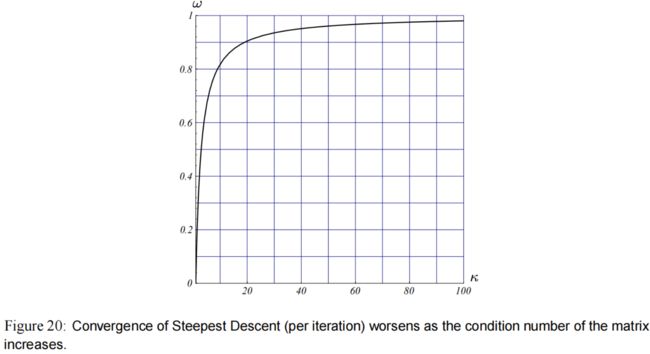
所以令 μ 2 = κ 2 \mu^2 = \kappa^2 μ2=κ2,你就能找到 ω \omega ω 的上边界(对应于最糟糕的起点): ω 2 ≤ 1 − 4 κ 4 κ 5 + 2 κ 4 + κ 3 = 1 − κ 5 − 2 κ 4 + κ 3 κ 5 + 2 κ 4 + κ 3 = ( κ − 1 ) 2 ( κ + 1 ) 2 ω 2 ≤ κ − 1 κ + 1 (27) \begin{aligned} \omega^2 & \leq 1 - \frac{4 \kappa^4}{ \kappa^5 +2\kappa^4 +\kappa^3 } \\[1em] & = 1 - \frac{ \kappa^5 - 2\kappa^4 + \kappa^3}{ \kappa^5 +2\kappa^4 +\kappa^3 } \\[1em] & = \frac{(\kappa - 1)^2}{ (\kappa + 1) ^2} \\[1em] \omega^2 & \leq \frac{ \kappa - 1 }{ \kappa + 1 } \end{aligned} \tag{27} ω2ω2≤1−κ5+2κ4+κ34κ4=1−κ5+2κ4+κ3κ5−2κ4+κ3=(κ+1)2(κ−1)2≤κ+1κ−1(27)
式(27) 的不等式如 图(20) 所示,如果矩阵越病态(ill-conditioned)(即条件数 κ \kappa κ 越大),则最陡下降的收敛越慢。
在 9.2节 中证明了当 n > 2 n>2 n>2 时 式子(27) 依然成立。
如果对称且正定的矩阵的条件数被定义为: κ = λ m a x λ m i n \kappa = \frac{\lambda_{max}}{\lambda_{min}} κ=λminλmax即最大的特征值比最小的特征值,则最速下降的收敛结果为: ∥ e ( i ) ∥ A ≤ ( κ − 1 κ + 1 ) i ∥ e ( 0 ) ∥ A (28) \| e_{(i)} \| _A \leq \left( \frac{\kappa -1}{\kappa+1} \right)^i \| e_{(0)} \| _A \tag{28} ∥e(i)∥A≤(κ+1κ−1)i∥e(0)∥A(28)
f ( x ( i ) ) − f ( x ) f ( x ( 0 ) ) − f ( x ) = 1 2 e ( i ) T A e ( i ) 1 2 e ( 0 ) T A e ( 0 ) (by equation 8) = ( κ − 1 κ + 1 ) 2 i \begin{aligned} \frac{ f(x_{(i)}) - f(x) }{ f(x_{(0)}) -f(x) } &= \frac{ \frac{1}{2} e_{(i)}^T A e_{(i)} }{ \frac{1}{2} e_{(0)}^T A e_{(0)} } \qquad \text{(by equation 8)} \\[1em] &= \left( \frac{ \kappa - 1 }{ \kappa + 1 } \right)^{2i} \end{aligned} f(x(0))−f(x)f(x(i))−f(x)=21e(0)TAe(0)21e(i)TAe(i)(by equation 8)=(κ+1κ−1)2i
7. The Method of Conjugate Directions(共轭方向)
7.1 Conjugacy(共轭性)
最陡下降经常发现它自己走的方向和先前几步的方向相同(见 图(8))。
(最速下降每一步的方向是当前位置的导数的反方向)
那这样会不会好点呢:我们选择其它的方向,并且每次我们迈出步伐时,在该方向上一步到位。
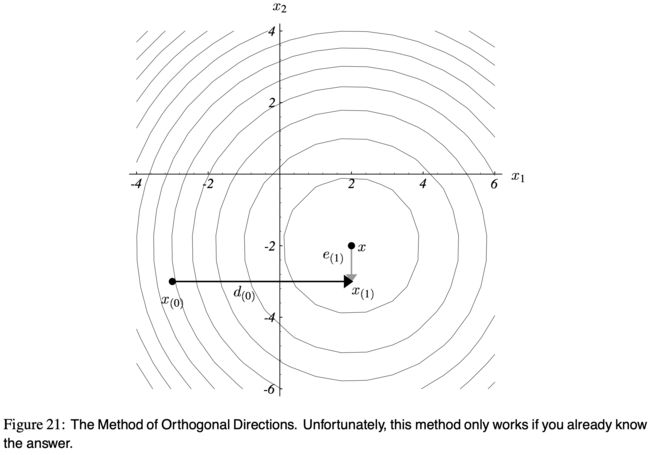
这里有一个想法:我们取一组正交的搜索方向(search directions): d ( 0 ) , d ( 1 ) , … , d ( n − 1 ) d_{(0)},d_{(1)},\dots,d_{(n-1)} d(0),d(1),…,d(n−1)。在每个搜索方向上,我们只需要走 1 1 1 步,这一步的长度正好与 x x x 成一条直线。迭代 n n n 步之后就搞定了。
图(21) 展示了这一思想,这个例子把 2 2 2 个坐标轴当作搜索方向。
第一步(水平方向)在 x 1 x_1 x1 的坐标轴上走到了正确的地方;
第二步(竖直方向, x 2 x_2 x2 的轴)直接到达终点。
每个方向只需 1 1 1 步。
值得注意的是,误差 e ( 1 ) e_{(1)} e(1) 的方向与搜索方向 d ( 0 ) d_{(0)} d(0) 是正交的。
总的来说,每一步我们走到的点就是: x ( i + 1 ) = x ( i ) + α ( i ) d ( i ) (29) x_{(i+1)} = x_{(i)} + \alpha_{(i)}d_{(i)}\tag{29} x(i+1)=x(i)+α(i)d(i)(29)
为了找到 α ( i ) \alpha_{(i)} α(i) 的值,利用条件 “ e ( i + 1 ) e_{(i+1)} e(i+1) 应当与 d ( i ) d_{(i)} d(i) 正交” ,于是走完这一步后,再也不需要在 d ( i ) d_{(i)} d(i) 的方向上前进了。利用这个条件,有: d ( i ) T e ( i + 1 ) = 0 d ( i ) T ( e ( i ) + α ( i ) d ( i ) ) = 0 (by Equation 29) α ( i ) = − d ( i ) T e ( i ) d ( i ) T d ( i ) (30) \begin{aligned} d_{(i)}^T e_{{(i+1)}} &= 0 \\ d_{(i)}^T ( e_{(i)} + \alpha_{(i)} d_{(i)}) &= 0 \qquad \text{(by Equation 29)} \\[0.5em] \alpha_{(i)} &= - \dfrac{d_{(i)}^T e_{(i)}}{ d_{(i)}^T d_{(i)} } \end{aligned} \tag{30} d(i)Te(i+1)d(i)T(e(i)+α(i)d(i))α(i)=0=0(by Equation 29)=−d(i)Td(i)d(i)Te(i)(30)
很遗憾,我们还有一些东西没有完成。
如果不知道 e ( i ) e_{(i)} e(i),就没办法算 α ( i ) \alpha_{(i)} α(i)。
然而,要是知道了 e ( i ) e_{(i)} e(i),那这个问题都已经有解了。
所以,现在的做法是,使搜索方向 A A A-正交(A-orthogonal)。
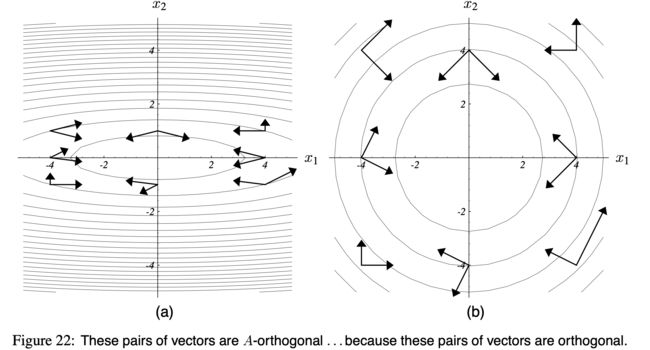
如果满足: d ( i ) T A d ( j ) = 0 d^T_{(i)} A d_{(j)} = 0 d(i)TAd(j)=0 则称向量 d ( i ) d_{(i)} d(i) 和向量 d ( j ) d_{(j)} d(j) 是 A A A-正交的。或者叫 共轭(conjugate)。
图(22)a 展示了 A A A-正交的向量是什么样子。想象这张图片是打印在一个泡泡球上,然后你拽着两端拉它,直到椭圆变成圆形。然后这些向量就成了正交的了,如 图(22)b。
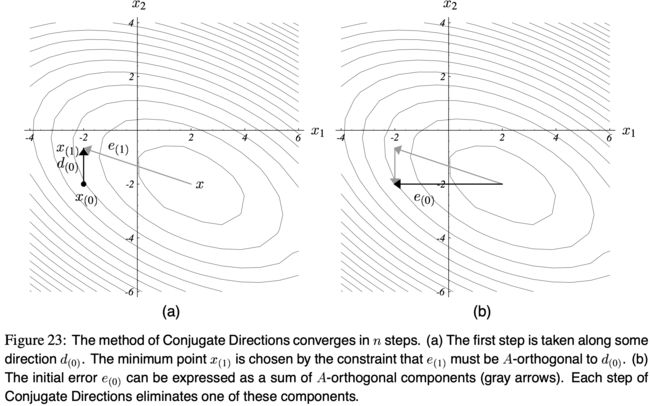
我们现在的要求是,要 e ( i + 1 ) e_{(i+1)} e(i+1) A A A-正交于 d ( i ) d_{(i)} d(i)。见图(23)a。
翻译一下 图(23) 的说明:
共轭方向法用 n n n 步就收敛。
图(a):第1步沿着 d 0 d_{0} d0 的方向走,走到最小值点 x ( 1 ) x_{(1)} x(1)。 x ( 1 ) x_{(1)} x(1) 怎么选?在那一点要满足 e ( 1 ) e_{(1)} e(1) 与 d ( 0 ) d_{(0)} d(0) A A A-正交。也就是 e ( 1 ) T A d ( 0 ) = 0 e_{(1)}^T A d_{(0)} = 0 e(1)TAd(0)=0。
图(b):初始误差 e ( 0 ) e_{(0)} e(0) 可以表示为一组 A A A-正交 的向量(或者叫做组件,components)的和,如图中灰色的线。在共轭方向法中,每走一步,就能消掉其中一个组件。
这个正交性条件恰好等价于,沿着搜索方向 d ( i ) d_{(i)} d(i) 寻找最小点,就像最陡下降那样。
为了看到这一结论,把方向导数设为 0 0 0:
d d α f ( x ( i + 1 ) ) = 0 f ′ ( x ( i + 1 ) ) T d d α x ( i + 1 ) = 0 − r ( i + 1 ) T d ( i ) = 0 d ( i ) T A e ( i + 1 ) = 0 \begin{aligned} \frac{d}{d\alpha}f\left( x_{(i+1)} \right) &= 0 \\[0.5em] f' \left( x_{(i+1)} \right)^T \frac{d}{d\alpha} x_{(i+1)} &= 0 \\[1em] -r^T_{(i+1)} d_{(i)} &= 0 \\[0.5em] d_{(i)}^T A e_{(i+1)} &= 0 \end{aligned} dαdf(x(i+1))f′(x(i+1))Tdαdx(i+1)−r(i+1)Td(i)d(i)TAe(i+1)=0=0=0=0
可以看到 e ( i + 1 ) e_{(i+1)} e(i+1) 和 d ( i ) d_{(i)} d(i) 是 A A A-正交的。
按照公式(30)的推导过程,再把 e ( i + 1 ) = e ( i ) + α ( i ) d ( i ) e_{(i+1)} = e_{(i)} + \alpha_{(i)} d_{(i)} e(i+1)=e(i)+α(i)d(i) 代到 d ( i ) T A e ( i + 1 ) = 0 d_{(i)}^T A e_{(i+1)}=0 d(i)TAe(i+1)=0 得:
α ( i ) = − d ( i ) T A e ( i ) d ( i ) T A d ( i ) ( 31 ) = − d ( i ) T r ( i ) d ( i ) T A d ( i ) ( 32 ) \begin{aligned} \alpha_{(i)} &= - \dfrac{ d_{(i)}^T A e_{(i)} }{ d_{(i)}^T A d_{(i)} } \qquad \qquad (31)\\[1.5em] &= - \dfrac{ d_{(i)}^T r_{(i)} }{ d_{(i)}^T A d_{(i)} } \qquad \qquad (32) \end{aligned} α(i)=−d(i)TAd(i)d(i)TAe(i)(31)=−d(i)TAd(i)d(i)Tr(i)(32)
不像 公式(30),上面的式子是可以算的。
值得注意的是,要是搜索向量(即搜索方向, d d d)刚好是残差,那这个公式就和最陡下降的公式(见式子(11))一样了。
为了证明确实只需要 n n n 步,我们把误差项 e e e 表示为搜索方向 d d d 的线性组合,即: e ( 0 ) = ∑ j = 0 n − 1 δ j d ( j ) (33) e_{(0)} = \sum^{n-1}_{j=0} \delta_j d_{(j)} \tag{33} e(0)=j=0∑n−1δjd(j)(33)
δ j \delta_j δj 的值可以利用一个数学的技巧来找到。
由于搜索方向是 A A A-正交的,可以对 式(33) 左乘 d ( k ) T A d_{(k)}^T A d(k)TA 来消掉 δ j \delta_j δj:
d ( k ) T A e ( 0 ) = ∑ j δ ( j ) d ( k ) T A d ( j ) d ( k ) T A e ( 0 ) = δ ( k ) d ( k ) T A d ( k ) (by A-orthogonality of d vectors) δ ( k ) = d ( k ) T A e ( 0 ) d ( k ) T A d ( k ) = d ( k ) T A e ( 0 ) + d ( k ) T A ( ∑ i = 0 k − 1 α ( i ) d ( i ) ) d ( k ) T A d ( k ) (by A-orthogonality of d vectors) = d ( k ) T A ( e ( 0 ) + ∑ i = 0 k − 1 α ( i ) d ( i ) ) d ( k ) T A d ( k ) = d ( k ) T A e ( k ) d ( k ) T A d ( k ) (by Equation 29) (34) \begin{aligned} d_{(k)}^T A e_{(0)} &= \sum_j \delta_{(j)} d_{(k)}^T A d_{(j)} \\[0.5em] d_{(k)}^T A e_{(0)} &= \delta_{(k)} d_{(k)}^T A d_{(k)} \qquad \text{(by A-orthogonality of d vectors) } \\[0.5em] \delta_{(k)} &= \frac{d_{(k)}^T A e_{(0)} }{ d_{(k)}^T A d_{(k)} } \\[0.5em] &= \frac{d_{(k)}^T A e_{(0)} + d_{(k)}^T A \left( \sum_{i=0}^{k-1} \alpha_{(i)} d_{(i)} \right) }{ d_{(k)}^T A d_{(k)} } \qquad \text{(by A-orthogonality of d vectors) } \\[0.5em] &= \frac{d_{(k)}^T A \left( e_{(0)}+ \sum_{i=0}^{k-1} \alpha_{(i)} d_{(i)} \right) }{ d_{(k)}^T A d_{(k)} } \\[0.5em] &= \frac{d_{(k)}^T A e_{(k)} }{ d_{(k)}^T A d_{(k)} } \qquad \text{(by Equation 29) } \end{aligned} \tag{34} d(k)TAe(0)d(k)TAe(0)δ(k)=j∑δ(j)d(k)TAd(j)=δ(k)d(k)TAd(k)(by A-orthogonality of d vectors) =d(k)TAd(k)d(k)TAe(0)=d(k)TAd(k)d(k)TAe(0)+d(k)TA(∑i=0k−1α(i)d(i))(by A-orthogonality of d vectors) =d(k)TAd(k)d(k)TA(e(0)+∑i=0k−1α(i)d(i))=d(k)TAd(k)d(k)TAe(k)(by Equation 29) (34)
通过 式(31) 和 式(34),我们发现 α ( i ) = − δ ( i ) \alpha_{(i)} = - \delta_{(i)} α(i)=−δ(i)。
这一现象让我们有一种新的方式看待误差项。
如下面的公式所示,一个组件一个组件地构建 x x x 的过程也可以看作是一个组件一个组件地减少误差项的过程(见 图(23)b)。
e ( i ) = e ( 0 ) + ∑ j = 0 i − 1 α ( j ) d ( j ) (by Equation 33 and α ( i ) = − δ ( i ) ) = ∑ j = 0 n − 1 δ ( j ) d ( j ) − ∑ j = 0 i − 1 δ ( j ) d ( j ) = ∑ j = i n − 1 δ ( j ) d ( j ) (35) \begin{aligned} e_{(i)} &= e_{(0)} + \sum^{i-1}_{j=0} \alpha_{(j)} d_{(j)} \qquad \text{(by Equation 33 and} \; \; \alpha_{(i)} = - \delta_{(i)} \text{)}\\[0.5em] &= \sum^{n-1}_{j=0} \delta_{(j)} d_{(j)} - \sum^{i-1}_{j=0} \delta_{(j)} d_{(j)} \\[0.5em] &= \sum^{n-1}_{j=i} \delta_{(j)} d_{(j)} \end{aligned} \tag{35} e(i)=e(0)+j=0∑i−1α(j)d(j)(by Equation 33 andα(i)=−δ(i))=j=0∑n−1δ(j)d(j)−j=0∑i−1δ(j)d(j)=j=i∑n−1δ(j)d(j)(35)
经过 n n n 步迭代,每一个组件都被干掉了,最后 e ( n ) = 0 e_{(n)} =0 e(n)=0,证明完毕。
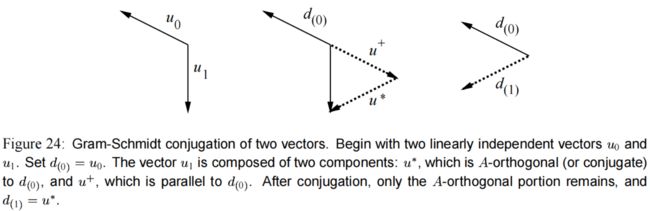
7.2 Gram-Schmidt Conjugation(格拉姆-施密特共轭)
我们现在所需要的是,找到一组 A A A-正交的搜索方向 { d ( i ) } \{d_{(i)}\} {d(i)}。
幸运的是,有一种简单的方法可以生成它们,叫做 共轭格拉姆-施密特过程(conjugate Gram-Schmidt process)。
假设我们有一组 n n n 个线性无关的向量 u 0 , u 1 , … , u n − 1 u_0, u_1,\dots,u_{n-1} u0,u1,…,un−1。
假设 (2维的情况) 其中某个 u i u_i ui 由 2 2 2 个组件线性组合而成,一部分是 u ∗ u^{*} u∗,另一部分是 u + u^+ u+。
为了构建 d ( i ) d_{(i)} d(i),令 u i u_i ui 减掉自己 【与 d ( i − 1 ) d_{(i-1)} d(i−1) 非 A A A-正交 】的那个组件(即 图(24) 中的 u + u^+ u+)。
翻译一下 图(24) 的说明:
俩向量的格拉姆-施密特共轭。
首先,从两个线性无关的向量( u 0 u_0 u0 和 u 1 u_1 u1)开始。令第一个方向向量 d ( 0 ) = u 0 d_{(0)}=u_0 d(0)=u0。
然后, u 1 u_1 u1 由两个组件组成:① u ∗ u^* u∗,它与 d ( 0 ) d_{(0)} d(0) 是 A A A-正交的(或者称 ‘共轭’ )。② u + u^+ u+,它与 d ( 0 ) d_{(0)} d(0) 是平行的。
共轭完成之后,只保留 A A A-正交部分, d ( 1 ) = u ∗ d_{(1)}=u^* d(1)=u∗。
用公式表达就是,先令 d ( 0 ) = u 0 d_{(0)}=u_0 d(0)=u0,然后对于 i > 0 i>0 i>0,令: d ( i ) = u i + ∑ k = 0 i − 1 β i k d ( k ) d_{(i)} = u_i + \sum^{i-1}_{k=0} \beta_{ik} d_{(k)} d(i)=ui+k=0∑i−1βikd(k) 其中, i > k i>k i>k 的情况才有 β i k \beta_{ik} βik。
这个式子看着很绕,这个 β \beta β 有 2 2 2 个下标,可以试着展开看来理解。假设 i i i 为 4 4 4,也就是 4 4 4 维:
d ( 0 ) = u ( 0 ) d ( 1 ) = u ( 1 ) + ( β 10 d ( 0 ) ) d ( 2 ) = u ( 2 ) + ( β 20 d ( 0 ) + β 21 d ( 1 ) ) d ( 3 ) = u ( 3 ) + ( β 30 d ( 0 ) + β 31 d ( 1 ) + β 32 d ( 2 ) ) \begin{aligned} d_{(0)} &= u_{(0)} \\ d_{(1)} &= u_{(1)} + \left( \beta_{10} d_{(0)} \right) \\ d_{(2)} &= u_{(2)} + \left( \beta_{20} d_{(0)} + \beta_{21} d_{(1)} \right) \\ d_{(3)} &= u_{(3)} + \left( \beta_{30} d_{(0)} + \beta_{31} d_{(1)} + \beta_{32} d_{(2)} \right) \end{aligned} d(0)d(1)d(2)d(3)=u(0)=u(1)+(β10d(0))=u(2)+(β20d(0)+β21d(1))=u(3)+(β30d(0)+β31d(1)+β32d(2))
为了找到这些值,用回之前求 ξ j \xi_j ξj 的技巧:
d ( i ) T A d ( j ) = u i T A d ( j ) + ∑ k = 0 i − 1 β i k d ( k ) T A d ( j ) 0 = u i T A d ( j ) + β i j d ( j ) T A d ( j ) , i > j (by A-orthogonality of d vectors) β i j = − u i T A d ( j ) d ( j ) T A d ( j ) (37) \begin{aligned} d_{(i)}^T A d_{(j)} &= u_i^T A d_{(j)} + \sum_{k=0}^{i-1} \beta_{ik} d_{(k)}^T A d_{(j)} \\ 0 &= u_i^T A d_{(j)} + \beta_{ij} d_{(j)}^T A d_{(j)}, \qquad i>j \qquad \text{(by A-orthogonality of} \;d \; \text{vectors)} \\[0.5em] \beta_{ij} &= - \frac{u_i^T A d_{(j)}}{ d_{(j)}^T A d_{(j)} } \tag{37} \end{aligned} d(i)TAd(j)0βij=uiTAd(j)+k=0∑i−1βikd(k)TAd(j)=uiTAd(j)+βijd(j)TAd(j),i>j(by A-orthogonality ofdvectors)=−d(j)TAd(j)uiTAd(j)(37)
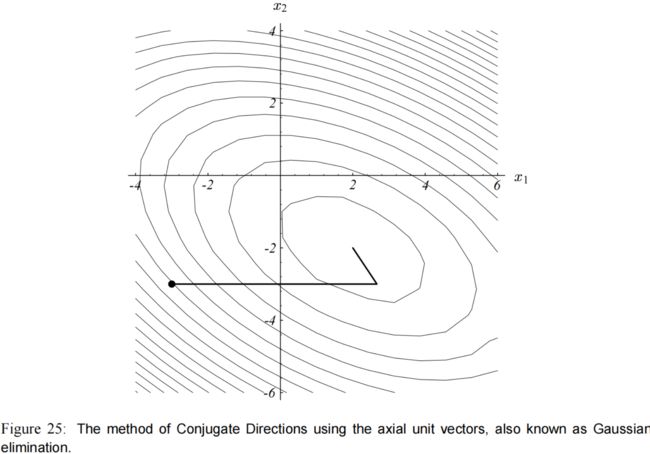
在共轭方向法 (Conjugate Directions)中应用格拉姆-施密特共轭 (Gram-Schmidt conjugation)的难点在于,之前所有的搜索向量都要保存在内存里,用于生成新的搜索向量。生成全部搜索向量的复杂度是 O ( n 3 ) \mathcal{O}(n^3) O(n3)
事实上,如果搜索向量是由轴向单位向量(axial unit vectors)的共轭来构造的,那么共轭方向(Conjugate Directions)就等价于执行高斯消元(Gaussian elimination),见 图(25)。
因此,在共轭梯度法(CG,Conjugate Gradient)被发现之前,共轭方向法(Conjugate Directions)很少被使用。CG 作为共轭方向法的一种,解决了这一问题。
理解共轭方向(以及共轭梯度)法的关键点是:图(25) 是 图(21) 的拉伸版!请记住,当你在执行共轭方向的方法时(或者共轭梯度法),此时你也是在一个拉伸了的空间上执行正交方向法(Orthogonal Directions)。
7.3 Optimality of the Error Term(误差项的最优性)
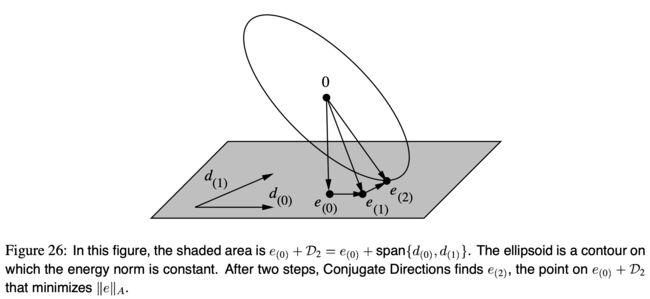
共轭方向法有一个有趣的特性:它在每一步都能在允许探索的范围内找到最优解。它能在哪里找呢?
令 D i D_i Di 为 i i i 维子空间张成的空间 { d ( 0 ) , d ( 1 ) , … , d ( i − 1 ) } \{d_{(0)}, d_{(1)}, \dots, d_{(i-1)}\} {d(0),d(1),…,d(i−1)}。
e ( i ) e_{(i)} e(i) 的值是从 e ( 0 ) + D i e_{(0)} + \mathcal{D}_i e(0)+Di 里选出来的。
我说的“最优解”是什么意思呢,意思是共轭方向法从 e ( 0 ) + D i e_{(0)} + \mathcal{D}_i e(0)+Di 选得一个值,使得 ∥ e ( i ) ∥ A \|e_{(i)} \|_A ∥e(i)∥A 最小。 见 图(26)。实际上,有一些作者是通过在 e ( 0 ) + D i e_{(0)} + \mathcal{D}_i e(0)+Di 中最小化 ∥ e ( i ) ∥ A \|e_{(i)} \|_A ∥e(i)∥A 来推导出共轭梯度法。
同样,误差项 e e e 可以表示为搜索方向 d d d 的线性组合。(公式(35) ) 它的能量范数可以表示为求和。
∥ e ( i ) ∥ A = ? = ( ∑ j = i n − 1 δ ( j ) d ( j ) ) T A ( ∑ k = i n − 1 δ ( k ) d ( k ) ) = ∑ j = i n − 1 ∑ k = i n − 1 δ ( j ) δ ( k ) d ( j ) T A d ( k ) (by Equation 35) = ∑ j = i n − 1 δ ( j ) 2 d ( j ) T A d ( j ) (by A-orthogonality of d vectors) \begin{aligned} \|e_{(i)} \|_A &= \quad ? \\ &= \left( \sum_{j=i}^{n-1} \delta_{(j)} d_{(j)} \right)^T A \left( \sum_{k=i}^{n-1} \delta_{(k)} d_{(k)} \right) \\ &= \sum_{j=i}^{n-1} \sum_{k=i}^{n-1} \delta_{(j)} \delta_{(k)} d_{(j)}^T A d_{(k)} \qquad \text{(by Equation 35)} \\ &= \sum_{j=i}^{n-1} \delta_{(j)}^{2} d_{(j)}^T A d_{(j)} \qquad \text{(by A-orthogonality of } d \; \text{vectors)} \end{aligned} ∥e(i)∥A=?=(j=i∑n−1δ(j)d(j))TA(k=i∑n−1δ(k)d(k))=j=i∑n−1k=i∑n−1δ(j)δ(k)d(j)TAd(k)(by Equation 35)=j=i∑n−1δ(j)2d(j)TAd(j)(by A-orthogonality of dvectors)
这个求和公式的每一项都是关于没有被遍历过的搜索方向。
在 e ( 0 ) + D i e_{(0)}+\mathcal{D}_i e(0)+Di 空间中选择任意其它的 e e e,其展开式中,也会有与上面求和公式中相同的项,因此 e ( i ) e_{(i)} e(i) 的能量范数一定是最小的。
(因为由于 A A A-正交,很多项被消掉了。其它的 e e e 还有很多项没有消掉,所以 e ( i ) e_{(i)} e(i) 比他们小。)
上面用公式证明了最优性,现在我们从直觉上来看看是怎么回事。想要把共轭方向的工作原理和过程可视化,也许最好的方法是对两个空间进行比较,一个是我们正在用的空间,另一个是 “拉伸了” 的空间,就像 图(22) 里那样。
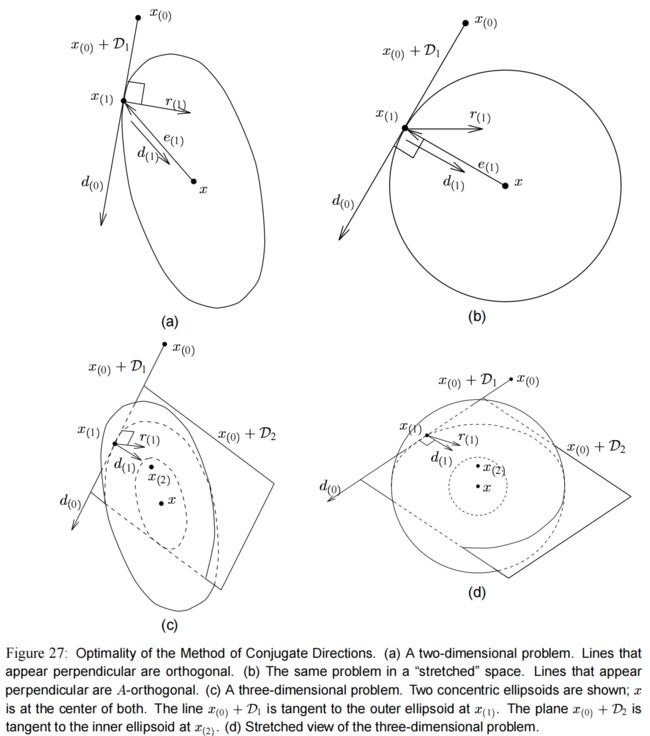
图(27)a 和 图(27)c 展示了共轭方向法在 R 2 \mathbb{R}^2 R2 和 R 3 \mathbb{R}^3 R3 上的特性,图示里垂直出现的线是正交的。
另外一方面,图(27)b 和 图(27)d 展示同样的画,但是它所在的空间是被拉伸过的(沿着特征向量的轴),因此等高线变成了圆形。
图里画的相互垂直的线都是 A A A-正交的。
在 图(27)a 里,共轭方向法从 x ( 0 ) x_{(0)} x(0) 开始,在 d ( 0 ) d_{(0)} d(0) 的方向上走一步,然后停在了 x ( 1 ) x_{(1)} x(1) 上,在那里的误差向量 e ( 1 ) e_{(1)} e(1) 与 d ( 0 ) d_{(0)} d(0) 是 A A A-正交的。为什么我们预期这里是 x ( 0 ) + D 1 x_{(0)}+\mathcal{D}_1 x(0)+D1 的最小值点呢?答案在 图(27)b 里:在这个拉伸的空间里, e ( 1 ) e_{(1)} e(1) 与 d ( 0 ) d_{(0)} d(0) 垂直,因为他们是 A A A-正交的。
误差向量 e ( 1 ) e_{(1)} e(1) 是一组同心圆的半径,这个 同心圆的轮廓由常量的 ∥ e ∥ A \|e\|_A ∥e∥A 形成。
因此, x ( 0 ) + D 1 x_{(0)}+\mathcal{D}_1 x(0)+D1 必定在 x ( 1 ) x_{(1)} x(1) 处与 x ( 1 ) x_{(1)} x(1) 所在的圆相切。
因此, x ( 1 ) x_{(1)} x(1) 就是在 x ( 0 ) + D 1 x_{(0)}+\mathcal{D}_1 x(0)+D1 空间上的能最小化 ∥ e ( 1 ) ∥ A \|e_{(1)}\|_A ∥e(1)∥A 的那个点。
个人理解:
对于 图(27)a, x ( 0 ) + D 1 x_{(0)} + \mathcal{D_1} x(0)+D1 这个空间是一条直线,第 1 1 1 步只能在这个空间上移动。
那么, x ( 1 ) x_{(1)} x(1) 降落在哪里,才能使 ∥ e ∥ A \|e\|_A ∥e∥A 最小呢?显然,是与同心圆相切的地方。
这并不奇怪,我们已经在 7.1 节见过, A A A-共轭( A A A-conjugacy)的搜索方向和误差项,等价于沿着搜索方向最小化 f f f(同样也是最小化 ∥ e ∥ A \|e\|_A ∥e∥A)。然而,在共轭方向法走了第 2 2 2 步之后,沿着第 2 2 2 个搜索方向 d ( 1 ) d_{(1)} d(1) 最小化 ∥ e ∥ A \|e\|_A ∥e∥A,为什么我们会预计 ∥ e ∥ A \|e\|_A ∥e∥A 在方向 d ( 0 ) d_{(0)} d(0) 上仍然是被最小化的呢?走完 i i i 步之后,为什么经过所有 x ( 0 ) + D i x_{(0)} + \mathcal{D}_i x(0)+Di 之后 f ( x ( i ) ) f(x_{(i)}) f(x(i)) 就是最小的呢?
在 图(27)b 里, d ( 0 ) d_{(0)} d(0) 和 d ( 1 ) d_{(1)} d(1) 表现为相互垂直,因为它们是 A A A-正交的。很明显 d ( 1 ) d_{(1)} d(1) 指向解 x x x,因为 d ( 0 ) d_{(0)} d(0) 在 x ( 1 ) x_{(1)} x(1) 处与圆心为 x x x 的圆正切。然而, 3 3 3 维的例子更有启发性。图(27)c 和 图(27)d 都各自展示了两个同心椭球体。 x ( 1 ) x_{(1)} x(1) 位于外面一层的球体上, x ( 2 ) x_{(2)} x(2) 位于里面那层的球体上。仔细观察这些图: x ( 0 ) + D 2 x_{(0)}+\mathcal{D}_2 x(0)+D2 这个平面切片穿过较大的椭球体,并在 x ( 2 ) x_{(2)} x(2) 处于小椭球体相切。 x x x 是球体的中心,在平面下面。
看着 图(27)c ,我们重新表述我们的问题。假设你和我都站在 x ( 1 ) x_{(1)} x(1) 处,想在 x ( 0 ) + D 2 x_{(0)} + \mathcal{D}_2 x(0)+D2 这个空间上走到某个位置,使得 ∥ e ∥ \|e\| ∥e∥ 最小。但我们只能沿着搜索方向 d ( 1 ) d_{(1)} d(1) 前进。如果 d ( 1 ) d_{(1)} d(1) 指向最小的点,那我们就成功了。有没有什么理由期望 d ( 1 ) d_{(1)} d(1) 会指向正确的方向呢?
图(27)d 给出了答案。由于 d ( 1 ) d_{(1)} d(1) 和 d ( 0 ) d_{(0)} d(0) 是 A A A-正交的,它们在这个图中是垂直的。现在,假设你盯着平面 x ( 0 ) + D 2 x_{(0)}+\mathcal{D}_2 x(0)+D2,就像它是一张纸一样;你所看到的景象将与 图(27)b 完全相同。点 x ( 2 ) x_{(2)} x(2) 将会在纸的中心,点 x x x 将会处于纸的正下方,直接就在点 x ( 2 ) x_{(2)} x(2) 正下面。因为 d ( 1 ) d_{(1)} d(1) 和 d ( 0 ) d_{(0)} d(0) 是垂直的, d ( 1 ) d_{(1)} d(1) 直接指向 x ( 2 ) x_{(2)} x(2),是在空间 x ( 0 ) + D 2 x_{(0)} + \mathcal{D}_2 x(0)+D2 里最靠近 x x x 的点。平面 x ( 0 ) + D 2 x_{(0)} + \mathcal{D}_2 x(0)+D2 与 x ( 2 ) x_{(2)} x(2) 所在的球面相切。如果你走第 3 3 3 步,就会直接从 x ( 2 ) x_{(2)} x(2) 下降到 x x x,在那个与 D 2 \mathcal{D}_2 D2 “ A A A-正交” 的方向上。
要用另外一种方式理解 图(27)d 发生了什么,你可以想像你正站在解那里(解就是 x x x),拉动一条连着珠子的绳子,这个珠子被限定在平面 x ( 0 ) + D i x_{(0)}+\mathcal{D}_i x(0)+Di 上。每当扩展子空间(expanding subspace) D \mathcal{D} D 被放大一个维度,珠子就可以自由地靠近你一点。如果你把这个空间拉成 图(27)c 那样,你就有了共轭方向法。
这个珠子的例子怎么解释呢?我是这样想的, x ( 0 ) + D 1 x_{(0)}+\mathcal{D}_1 x(0)+D1 这个空间是一条线, 1 1 1 维的。一开始珠子只能在这上面移动,所以就算把牵着珠子的线拉直了,珠子还是很远(在 x ( 1 ) x_{(1)} x(1) 的地方)。然后珠子的活动空间扩展了一个维度,可以在 x ( 0 ) + D 2 x_{(0)}+\mathcal{D}_2 x(0)+D2 这个空间上活动,这个空间是一个面, 2 2 2 维的。继续拉珠子上的线,拉直后珠子来到了 x ( 2 ) x_{(2)} x(2),离我们的 x x x 又更近了。最后,再扩展一个维度,珠子能够在整个 3 3 3 维空间上活动,这次再拉就把珠子拉到自己身边了,就到达了 x x x。
在这些插图中可以看到共轭方向的另一个重要性质,我们已经看到,在每一步中,超平面 x ( 0 ) + D i x_{(0)}+\mathcal{D}_i x(0)+Di 与 x ( i ) x_{(i)} x(i) 所处的椭球体正切。回想第4章,任意一点的残差与该点的椭球面正交,因此, r ( i ) r_{(i)} r(i) 也与 D i \mathcal{D}_i Di 正交。要用数学方法来证明这个现象,用 − d ( i ) T A -d_{(i)}^TA −d(i)TA 左乘 式子(35) 得: − d ( i ) T A e ( j ) = − ∑ j = i n − 1 δ ( j ) d ( i ) T A d ( j ) ( 38 ) d ( i ) T r ( j ) = 0 , i < j ( by A-orthogonality of d -vectors) ( 39 ) \begin{aligned} -d_{(i)}^TA e_{(j)}&= - \sum_{j=i}^{n-1} \delta_{(j)} d_{(i)}^TA d_{(j)} \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \; (38) \\ d_{(i)}^T r_{(j)} &= 0 , \qquad i
我们本可以通过另一种方法来推导出这个等式。回想一下,一旦我们朝着搜索方向迈出了一步,我们再也不需要朝着这个方向走了。误差项总是与所有旧的搜索方向 A A A-正交。由于 r ( i ) = − A e ( i ) r_{(i)} = -Ae_{(i)} r(i)=−Ae(i),残差永远与所有旧的搜索方向正交。
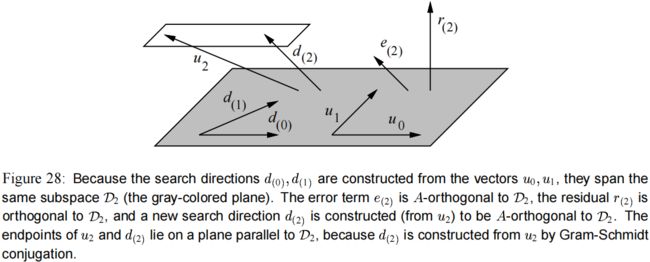
由于搜索方向都是从向量 u u u 构建而来的, u 0 , … , u i − 1 u_0, \dots,u_{i-1} u0,…,ui−1 跨越的子空间是 D i \mathcal{D}_i Di,残差 r ( i ) r_{(i)} r(i) 同样与前面这些 u u u 向量正交(见 图(28))。通过计算 式子(36) 与 r ( j ) r_{(j)} r(j) 的内积可以证明。 d ( i ) T r ( j ) = u i T r ( j ) + ∑ k = 0 i − 1 β i k d ( k ) T r ( j ) ( 40 ) 0 = u ( i ) T r ( j ) , i < j ( by Equation 39 ) ( 41 ) \begin{aligned} d_{(i)}^T r_{(j)} &= u_i^T r_{(j)} + \sum_{k=0}^{i-1} \beta_{ik} d_{(k)}^T r_{(j)} \qquad \qquad \qquad \qquad \qquad (40) \\ 0 &= u_{(i)}^T r_{(j)} , \qquad i
还有一个等式我们稍后会用到。从 式子(40) 和 图(28) 有:
d ( i ) T r ( i ) = u i T r ( i ) (42) d_{(i)}^T r_{(i)} = u_i^T r_{(i)} \tag{42} d(i)Tr(i)=uiTr(i)(42)
最后,注意到,与最陡下降法一样,通过使用递推求残差,可以将每次迭代的矩阵-向量乘法的数量减少为 1 1 1: r ( i + 1 ) = − A e ( i + 1 ) = − A ( e ( i ) + α ( i ) d ( i ) ) = r ( i ) − α ( i ) A d ( i ) (43) \begin{aligned} r_{(i+1)} &= -A e_{(i+1)} \\ &= -A ( e_{(i)} + \alpha_{(i)} d_{(i)} ) \\ &= r_{(i)} - \alpha_{(i)} A d_{(i)} \tag{43} \end{aligned} r(i+1)=−Ae(i+1)=−A(e(i)+α(i)d(i))=r(i)−α(i)Ad(i)(43)