共轭梯度法(Conjugate gradient)详解
1.什么是共轭向量
对于正定矩阵Q,如果有
x T Q y = 0 x^TQy = 0 xTQy=0
那么我们可以称x, y是关于Q-conjugate。
2.线性方程组求解与二次函数求极小值转化
最初,共轭梯度法是用来求解线性方程 A x = b Ax = b Ax=b的一种方法,特别是稀疏线性方程组迭代求解法里面最优秀的方法,其被称为线性共轭梯度法。后来,人们把这种方法慢慢推广到了非线性问题求解中,称为非线性共轭梯度法。
求解 A x = b Ax = b Ax=b时,最简单粗暴的方式为 x = A − 1 b x = A^{-1}b x=A−1b。但是这种方法的问题很明显:求逆矩阵的计算复杂度非常高。即使我们考虑用矩阵分解的方式,仍然会很慢。因此,我们尽可能考虑用迭代的方式,而不是直接求逆的方式来解这个问题。
如果构造一个二次函数:
f ( x ) = 1 2 x T A x − b T x f(x) = \frac{1}{2}x^TAx - b^Tx f(x)=21xTAx−bTx
对其求最小值,即令导数为零:
∇ f ( x ) = A x − b T = 0 \nabla f(x) = Ax - b^T = 0 ∇f(x)=Ax−bT=0
此时,正好是线性方程组 A x − b = 0 Ax - b = 0 Ax−b=0的解。因此,我们可以将线性方程组求解问题转化为二次函数求极小值问题。
3.求解过程
根据第二部分推导,将求线性方程组解的问题转化为求二次函数极小值
f ( x ) = 1 2 x T Q x − b T x f(x) = \frac{1}{2}x^TQx - b^Tx f(x)=21xTQx−bTx
结合第一部分,我们找到n个相互Q-conjugate的向量 d 1 , d 2 , d 3 , ⋯ , d n d_1, d_2, d_3, \cdots, d_n d1,d2,d3,⋯,dn,他们相互共轭且线性无关,则空间任意向量x可以用该组基向量表示:
x = ∑ i = 1 n a i d i x = \sum_{i=1} ^n a_i d_i x=i=1∑naidi
上面的目标函数f(x)可以表示为如下
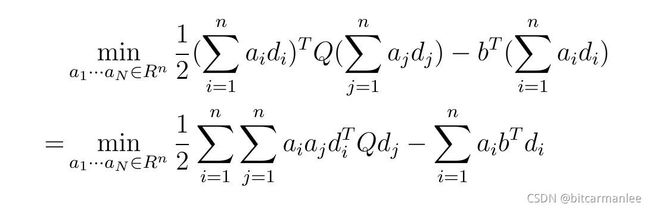
注意因为d是一组共轭向量,所以当 i ≠ j i \neq j i=j时,有 d i T Q d j = 0 d_i^TQd_j=0 diTQdj=0
上面的公式可以变为
m i n a 1 , ⋯ , a n ∈ R n 1 2 ∑ i = 1 n a i 2 d i T Q d i − ∑ i = 1 n a i b T d i \underset {a1,\cdots,a_n \in R^n}{min} \frac{1}{2} \sum_{i=1}^n a_i ^ 2 d_i ^TQd_i - \sum_{i=1}^na_ib^Td_i a1,⋯,an∈Rnmin21i=1∑nai2diTQdi−i=1∑naibTdi
进一步化简,
m i n a 1 , ⋯ , a n ∈ R n 1 2 ∑ i = 1 n ( a i 2 d i T Q d i − a i b T d i ) \underset {a1,\cdots,a_n \in R^n}{min} \frac{1}{2} \sum_{i=1}^n (a_i ^ 2 d_i ^TQd_i - a_ib^Td_i) a1,⋯,an∈Rnmin21i=1∑n(ai2diTQdi−aibTdi)
现在变量 a 1 , a 2 , ⋯ , a n a_1, a_2, \cdots, a_n a1,a2,⋯,an已经被分开了,将上面的式子再改写一下
m i n a 1 , ⋯ , a n ∈ R n 1 2 ( a 1 2 d 1 T Q d 1 − a 1 b T d 1 ) + 1 2 ( a 2 2 d 2 T Q d 2 − a 2 b T d 2 ) + ⋯ + 1 2 ( a n 2 d n T Q d n − a n b T d n ) \underset {a1,\cdots,a_n \in R^n}{min} \frac{1}{2} (a_1 ^ 2 d_1 ^TQd_1 - a_1b^Td_1) + \frac{1}{2} (a_2 ^ 2 d_2 ^TQd_2 - a_2b^Td_2) + \cdots + \frac{1}{2} (a_n ^ 2 d_n ^TQd_n - a_nb^Td_n) a1,⋯,an∈Rnmin21(a12d1TQd1−a1bTd1)+21(a22d2TQd2−a2bTd2)+⋯+21(an2dnTQdn−anbTdn)
这样,我们可以分别求每一项的最小值。比如第一项求最小值,直接求导即可:
a 1 d 1 T Q d 1 − b T d 1 = 0 a_1 d_1^TQ d_1 - b^T d_1 = 0 a1d1TQd1−bTd1=0
则可得:
a 1 = b T d 1 d 1 T Q d 1 a_1 = \frac{b^T d_1}{d_1^TQ d_1} a1=d1TQd1bTd1
对于每一项,都有
a i = b T d i d i T Q d i a_i = \frac{b^T d_i}{d_i^TQ d_i} ai=diTQdibTdi
所以最终的最优解为:
x ∗ = ∑ i = 1 n a i d i x^* = \sum_{i=1}^n a_i d_i x∗=i=1∑naidi
即:
x ∗ = ∑ i = 1 n b T d i d i T Q d i d i x^* = \sum_{i=1}^n \frac{b^T d_i}{d_i^TQ d_i} d_i x∗=i=1∑ndiTQdibTdidi
4.共轭梯度法的精髓
回顾上述的推导过程来看,共轭梯度法就是把目标函数分成许多方向,然后不同方向分别求出极值在综合起来。
如果是二次优化问题,共轭梯度法理论上是可以保证最多n步一定找到最优解。
共轭梯度法仅利用了函数的一阶导数信息,但是克服了梯度下降收敛慢的缺点,同时又避免了牛顿法求二阶导计算量大的问题,不仅是解决大型线性方程组最有用的方法之一,也是解大型非线性最优化最有效的算法之一。当然,缺点就是前面我们提到的,是专门针对二次优化问题,其他场景不太适用。