2022 年杭电多校第七场补题记录
A Bowling
题意:给定平面上一 n n n 顶点凸多边形,和 m m m 个点, q q q 次询问,每次给定一个方向向量 v ⃗ \vec v v,问该凸多边形以该方向向量移动会碰到几个点。 n , m , q ≤ 1 × 1 0 5 n,m,q \leq 1\times 10^5 n,m,q≤1×105。
解法:不妨考虑点向凸包移动。则一个点会撞击到凸包等效于该方向向量处于该点看凸包的视角范围内。因而对每个点以 O ( log n ) \mathcal O(\log n) O(logn) 的复杂度求出它到凸多边形的切线,记录每个点的视角范围(必然为至多两个连续区间,可以根据 x x x 轴负向为分界点),则变成一区间问题——查询对应的方向向量被多少个区间覆盖。使用前缀和即可。总复杂度 O ( m log n + q ) \mathcal O(m \log n+q) O(mlogn+q)。
vector<int> solve(const Convex &ball, const vector<Point> &pins, const vector<Point> &ques)
{
auto dirs=ques; dirs.reserve(ques.size()+pins.size()+pins.size());
vector<pair<size_t,size_t>> tans; tans.reserve(pins.size());
for (const auto &pin:pins)
{
const auto t=ball.tangent(pin);
const auto i=t.first,j=t.second;
tans.push_back(t);
dirs.push_back(pin-ball.p[j]);
dirs.push_back(pin-ball.p[i]);
}
sort(dirs.begin(),dirs.end(),argcmp());
const auto eq=[&](const Point &u,const Point &v){return u*v>eps && abs(u^v)<=eps;};
dirs.erase(unique(dirs.begin(),dirs.end(),eq),dirs.end());
const int siz=dirs.size();
vector<int> diff(siz),sum(siz);
for (size_t i=0;i<pins.size();i++)
{
const auto pin=pins[i];
const auto t=tans[i];
const Point u=pin-ball.p[t.second],v=pin-ball.p[t.first];
const int l=lower_bound(dirs.begin(),dirs.end(),u,argcmp())-dirs.begin();
const int r=lower_bound(dirs.begin(),dirs.end(),v,argcmp())-dirs.begin();
if (l<=r)
{
diff[l]++;
if (r+1<siz) diff[r+1]--;
}
else
{
diff[l]++; diff[0]++;
if (r+1<siz) diff[r+1]--;
}
}
partial_sum(diff.begin(),diff.end(),sum.begin());
vector<int> ans; ans.reserve(ques.size());
for (const auto &que:ques)
{
const int i=lower_bound(dirs.begin(),dirs.end(),que,argcmp())-dirs.begin();
ans.push_back(sum[i]);
}
return ans;
}
B Independent Feedback Vertex Set
题意:通过如下方式构造一个 n n n 个点的图:首先有三点 1 , 2 , 3 1,2,3 1,2,3,互相相连;此外再依次加入 n − 3 n-3 n−3 个点,每个点 i i i 恰与之前已经直接连通的两点 u , v u,v u,v 构成三元环——即每加入一个点新增两条边 ( u , i ) , ( v , i ) (u,i),(v,i) (u,i),(v,i)。在这个图上,每个点有一个权值 a i a_i ai,要求从该图中选出一个点的子集 V V V,使得 V V V 中任意两点没有直接的边相连,且 U / V U/V U/V 为一个森林,最大化 V V V 中点权值和。 n ≤ 5 × 1 0 5 n \leq 5\times 10^5 n≤5×105。
解法:容易注意到, V V V 集合必然包含每个三元环中恰好一个点,因而 1 , 2 , 3 1,2,3 1,2,3 中恰好只能选一个,这时对图做三染色(让每个三元环三个点颜色均不相同)即可。总时间复杂度 O ( n ) \mathcal O(n) O(n)。
#include C Counting Stickmen
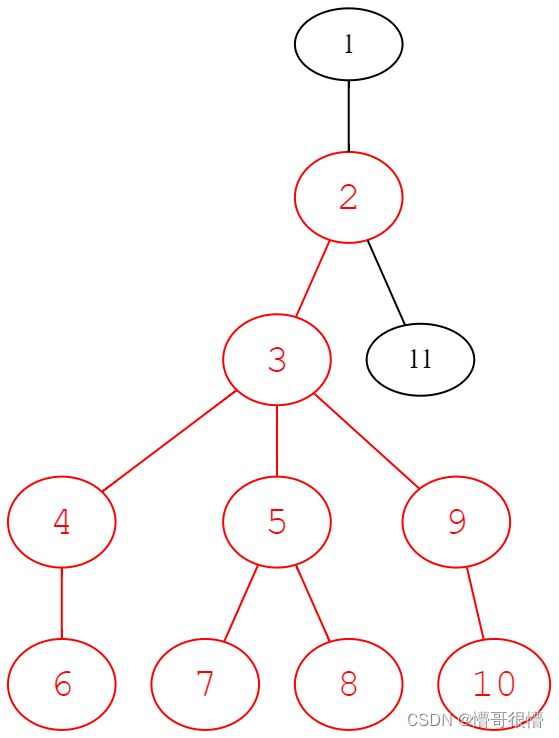
题意:给定一棵 n n n 个点以 1 1 1 为根的树,问树上节点能构成火柴人的有多少个。 n ≤ 5 × 1 0 5 n \leq 5\times 10^5 n≤5×105。火柴人如下图红色点所示:
解法:枚举图中 3 3 3 号点(脖子)的情况。从该点开始,任意与之相连的点均可做头,与之相连的度数大于等于 2 2 2 的可以做手,度数大于等于 3 3 3 的可以做身体。因而总的方案为选一个做头,选两个做手,选一个做身体。但是存在一个情况:翻花手,即两条手臂相同,只是手不同,例如以 3 − 5 − 7 3-5-7 3−5−7 和 3 − 5 − 8 3-5-8 3−5−8 做手,这是不允许的。那么这种情况容易注意到其实就是身体,扣除这种情况即可。
在实际的操作中,维护一个 h e a d \rm head head 数组表示以 i i i 节点为脖子,头有几个, b o d y \rm body body 表示以 i i i 为脖子,身体有几种。枚举每个度大于等于 4 4 4 的节点作为脖子进行计算即可。
#include D Black Magic
题意:有 E E E 种两面全白的方块, L L L 种左黑右白的方块, R R R 种左白右黑的方块, B B B 种两侧都黑的方块。现在将他们重新排列,相邻两侧(左侧方块的右侧和右侧方块的左侧)若均为黑色和两方块合并变成一个。方块不能旋转,问最多和最少能变成几个方块。
解法:注意到 B + L = L B+L=L B+L=L, R + B = R R+B=R R+B=R, L + R = E L+R=E L+R=E。对于最少方块数目,则必然是 L , R L,R L,R 成对变成一个 E E E。因而答案为 min ( L , R ) + E \min(L,R)+E min(L,R)+E。若无 L , R L,R L,R,则所有 B B B 合成为一个,答案为 E + [ B ] E+[B] E+[B]。
对于最多方块数目,必然是左侧全部放 L L L,右侧全部放 R R R,最后 E B E B EBEB EBEB 的摆放。注意 L , R L,R L,R 交接处有一个放 B B B 而不会合并的机会。
#include F Sumire
题意:给定 l , r , k , B , d l,r,k,B,d l,r,k,B,d,计算 ∑ i = l r f k ( i , B , d ) \displaystyle \sum_{i=l}^rf^k(i,B,d) i=l∑rfk(i,B,d),其中 f ( i , B , d ) f(i,B,d) f(i,B,d) 表示数字 i i i 在 B B B 进制下数码 d d d 出现次数,不含前导零。 T T T 组测试数据, 1 ≤ l ≤ r ≤ 1 × 1 0 18 1 \leq l \leq r \leq 1\times 10^{18} 1≤l≤r≤1×1018, 0 ≤ d < B ≤ 1 × 1 0 9 0 \leq d < B \leq 1\times 10^9 0≤d<B≤1×109, 0 ≤ k ≤ 1 0 9 0 \leq k \leq 10^9 0≤k≤109,定义 0 0 = 0 0^0=0 00=0。
解法:基础数位 dp。 g i , j , 0 / 1 , 0 / 1 g_{i,j,0/1,0/1} gi,j,0/1,0/1 表示当前在 B B B 进制下已经考虑到了第 i i i 位,已经出现了 j j j 个数码 d d d,是否有前导零,是否顶住上界,枚举当前位置应当填什么( 0 , d , u p 0,d,up 0,d,up 和其他四种情况)进行转移即可。
#include G Weighted Beautiful Tree
题意:给定一个 n n n 个点的树,树上每个点有权值 w i w_i wi 和费用 c i c_i ci 表示修改它的代价,即将其权值修改为 w i ′ w_i' wi′ 的代价为 c i ∣ w i ′ − w i ∣ c_i|w_i'-w_i| ci∣wi′−wi∣。树上每条边有权值 w e i we_i wei,连接了 u i , v i u_i,v_i ui,vi。现在要求树上每条边的权值 w e i we_i wei 满足 w e i ∈ [ min ( w u i ′ , w v i ′ ) , max ( w u i ′ , w v i ′ ) ] we_i \in [\min(w_{u_i}',w_{v_i}'),\max(w_{u_i}',w_{v_i}')] wei∈[min(wui′,wvi′),max(wui′,wvi′)],求最小修改代价。 n ≤ 1 × 1 0 5 n \leq 1\times 10^5 n≤1×105。
解法:考虑 f u , 0 / 1 f_{u,0/1} fu,0/1 表示 u u u 节点修改后,作为它连向父亲的边的最小值(即 w u ′ ≤ w e u , f a u w_u' \leq we_{u,fa_u} wu′≤weu,fau,用 0 0 0 记录)还是最大值(用 1 1 1 记录)。考虑 u u u 下全部的儿子 v v v,根据 ( u , v ) (u,v) (u,v) 和它连向它父亲的边权值可以将 u u u 的可选值域划分为 c h u + 1 ch_u+1 chu+1 段,在每一段它的转移是确定的,仅在恰好为边权的时候有两种情况。因而对 u u u 连向它儿子的边权从小到大的排序,然后从小到大的维护最小和值即可。对于边权相同的边需要一起处理。
#include H Triangle Game
题意:给定三个数字 a , b , c a,b,c a,b,c,初始时它们可以围成三角形。Alice 和 Bob 二人轮流将其中一个数字减小一个正整数,使得这三个数字仍能组成三角形三边,谁不能操作谁输。问输赢。 a , b , c ≤ 1 × 1 0 9 a,b,c \leq 1\times 10^9 a,b,c≤1×109。
解法:不妨令 a ≤ b ≤ c a \leq b \leq c a≤b≤c。若 a = 1 a=1 a=1 则先手必败。因而谁都不会让 a , b , c a,b,c a,b,c 率先出现 1 1 1,同时他们可以下对称棋,因而游戏可以规约到 Nim 游戏,判定方法即是 ( a − 1 ) ⊕ ( b − 1 ) ⊕ ( c − 1 ) (a-1) \oplus (b-1) \oplus (c-1) (a−1)⊕(b−1)⊕(c−1) 是否为 0 0 0。
#include I Counting Good Arrays
题意:求出长度不超过 n n n,最大值不超过 m m m 且满足 a i − 1 ∣ a i a_{i-1}|a_i ai−1∣ai 的序列 { a n } \{a_n\} {an} 个数。 n , m ≤ 1 × 1 0 9 n,m \leq 1\times 10^9 n,m≤1×109。
解法:令 f m , i f_{m,i} fm,i 表示最大值不超过 m m m,严格递增序列长度为 i i i 的个数,则:
f m , i ← ∑ d = 2 m f ⌊ m d ⌋ , i − 1 f_{m,i} \leftarrow \sum_{d=2}^m f_{\left \lfloor \frac{m}{d} \right \rfloor,i-1} fm,i←d=2∑mf⌊dm⌋,i−1
其具体含义为,对于一个最大值不超过 m m m 的长度为 i i i 的序列, a i a_i ai 必然是通过 a i − 1 a_{i-1} ai−1 乘以一个值 d d d 得到的,而 a i ≤ m a_i \leq m ai≤m 可得 a i − 1 ≤ ⌊ m d ⌋ a_{i-1} \leq \left \lfloor \dfrac{m}{d}\right \rfloor ai−1≤⌊dm⌋,且这个 d ≥ 2 d \geq 2 d≥2。不难发现, i ≤ log m i\leq \log m i≤logm,因而总的 dp 数组仅有 m log m \sqrt m \log m mlogm 个状态。但是如果朴素转移,从小到大的递推,则每个状态需要 O ( m log m ) O(m \log m) O(mlogm) 的复杂度,显然是不可接受的。这时考虑使用类似于 min_25 筛第一部分的递推,并对 m \sqrt m m 个状态进行 O ( 1 ) O(1) O(1) 的数组映射存储,即可将本步骤优化到 O ( m 3 4 ) O(m^{\frac{3}{4}}) O(m43)。
接下来是由严格递增序列恢复到原序列。考虑从中间插入数字,若原序列仅 i i i 个数字,则增补到不超过 n n n 个数字的总方案数为:
∑ k = i n ( k − 1 i − 1 ) = ∑ k = i n ( k − 1 k − i ) = ∑ k = 0 n − i ( i + k − 1 k ) = ( n i ) \begin{aligned} &\sum_{k=i}^n {k-1 \choose i-1}\\ =&\sum_{k=i}^n {k-1 \choose k-i}\\ =&\sum_{k=0}^{n-i}{i+k-1\choose k}={n \choose i} \end{aligned} ==k=i∑n(i−1k−1)k=i∑n(k−ik−1)k=0∑n−i(ki+k−1)=(in)
即考虑将原序列的 i − 1 i-1 i−1 个数字插入到长度为 k − 1 k-1 k−1 的数组中(第一个数字钦定放第一位),并对 k k k 求和,可得方案为 ( n i ) \displaystyle {n \choose i} (in),则答案为 ∑ i = 1 log m f m , i ( n i ) \displaystyle \sum_{i=1}^{\log m}f_{m,i}{n\choose i} i=1∑logmfm,i(in)。
说明:下面代码中的 f [ i ] [ m ] f[i][m] f[i][m] 数组其实是推导过程中的 f m , i ( m i ) \displaystyle f_{m,i}{m \choose i} fm,i(im)。
#include J Connectivity of Erdős-Rényi Graph
题意: q q q 次询问,每次给定一个 n n n 个点的无向完全图 K n K_n Kn,其中每条边以 a b \dfrac{a}{b} ba 的概率产生,问图的连通块期望个数。 q ≤ 1 × 1 0 5 q \leq 1\times 10^5 q≤1×105, n ≤ 5 × 1 0 5 n \leq 5\times 10^5 n≤5×105。
解法:(待补)