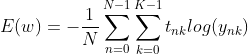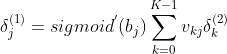神经网络(从手撕到工具包)
在学习神经网络之前，我认为弄懂逻辑回归是很有必要的(对于逻辑回归比较陌生的可以看看该作者分类那篇文章(●'◡'●))，因为逻辑回归就相当于神经网络的一个“神经元”，而整个神经网络就是由这些“神经元”构成的。我们知道每个"神经元"的作用是完成一个二分类的任务，那么将这些“神经元”链接起来自然而然是为了完成一个多分类的任务，这也就是神经网络的作用了。为了方便后面分享内容的理解，我们会先从一个神经元模型讲起，再到二层前馈神经网络，再和大家分享误差反向传播内容，最后与大家分享keras实现神经网络模型。希望能对大家有所帮助，如有错误，还望大家不吝指出。
目录
一、神经元模型
二、二层前馈神经网络
三、误差反向传播
四、使用Keras实现神经网络模型
五、文章代码合集
一、神经元模型
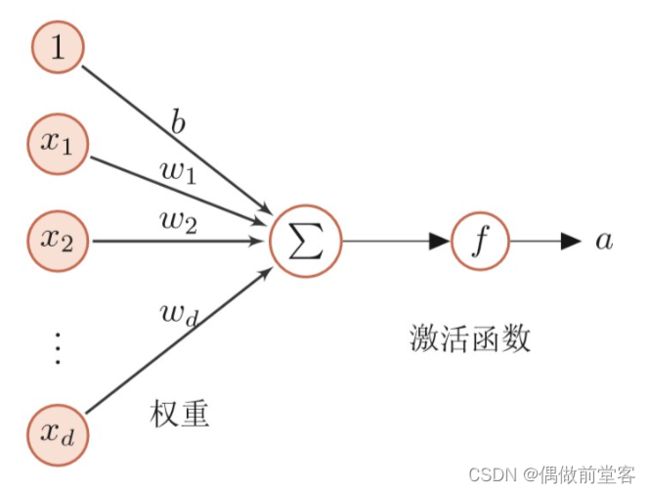
在神经元模型中有输入值x1，x2......xd(可以是正或负的实数值)，也有权重w1,w2.......wd(这里也可以叫它们为神经元的突触传递强度)，也有偏置值b，之后我们就会得到输入总和
(我们也管输入总和为膜电位)，最后我们通过激活函数sigmoid函数得到整个神经元的输出值a，a是0和1之间的连续值。正如我上述一样，一个逻辑回归模型就相当于一个神经元。并且与逻辑回归模型一样，神经元模型也是用平均交叉熵误差作为损失函数：
接下来我们将神经元拼接组合就得到了我们的神经网络。
二、二层前馈神经网络
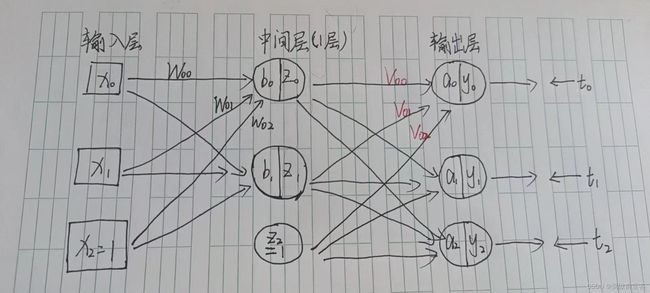
如上图所示的是一个二层前馈神经网络。有人把输入层也包含在内，认为它是三层的。考虑到权重参数只有W和V这两层，把它当作二层的做法似乎更为妥当。
这个神经网络接受二维
的输入，然后用三个神经元进行输出。我们要对网络进行训练，使得每个输出神经元的输出值能够代表数据属于每个类别的概率。b、a是输入总和，
是输入总和应用sigmoid函数后，得到中间层神经元的输出，但有一点需要注意，今后我们用的不一定是sigmoid函数，又可能使用别的函数，我们称这类函数为激活函数。这个中间层的输出决定了输出层的神经元的活动。输出层中的
是输入总和运用softmax函数后得到的输出。
使用了Softmax函数易知，输出
的和
等于1，因此就可以把这些值解释为概率了。这样我们就完成了网络功能的定义。上面的
是永远为1的虚拟神经元，这样做是为了让求和表达式中包含偏置项。
接下来，我们用代码来实现上面的神经网络。
我们先生成一些需要用到的数据。
import numpy as np
import matplotlib.pyplot as plt
np.random.seed(seed=1) #固定随机数
N = 200 #数据个数
K = 3 #分类个数
T = np.zeros((N,3),dtype=np.uint8)#dtype=np.uint8有利于加快运算速度
X = np.zeros((N,2))#生成二维数据
X_range0 = [-3,3]
X_range1 = [-3,3]
#有利于后面的画图
Mu = np.array([[-.5,-.5],[.5,1.0],[1,-.5]]) #分类的中心
Sig = np.array([[.7,.7],[.8,.3],[.3,.8]]) #分类的离散值
Pi = np.array([0.4,0.8,1]) #各分布所占的比例
for n in range(N):
wk = np.random.rand()
for k in range(K):
if wk < Pi[k]:
T[n, k] = 1
break
for k in range(2):
X[n,k] = np.random.randn() * Sig[T[n,:] == 1,k] + Mu[T[n,:] == 1,k]将数据分为训练数据X_train,T_train和测试数据X_test,T_test。为了验证是否发生过拟合。
TrainingRatio = 0.5
X_n_training = int(N * TrainingRatio)
X_train = X[:X_n_training,:]
X_test = X[X_n_training:,:]
T_train = T[:X_n_training,:]
T_test = T[X_n_training:,:]然后我们将训练集和测试集可视化
def Show_data(x,t):
wk,n = t.shape
for i in range(n):
plt.plot(x[t[:,i] == 1,0],x[t[:,i] == 1,1],marker='o',linestyle='none',alpha=0.8)
plt.grid(True)
plt.subplot(1,2,1)
Show_data(X_train,T_train)
plt.xlim(X_range0)
plt.ylim(X_range1)
plt.title('Training Data')
plt.subplot(1,2,2)
Show_data(X_test,T_test)
plt.xlim(X_range0)
plt.ylim(X_range1)
plt.title('Test Data')
plt.show()我们把二层前馈神经网络的函数命名为FNN。FNN接收传给网络的输入x，输出y。输入x是D维向量，输出y是K维向量，目前我们探讨的是D=2，K=3的情况。我们希望网络的函数FNN能够一次处理N(这里的N=100)个数据，因此将x作为数据量N*D维的矩阵，将y作为数据量N*K维的矩阵。向量y[n,0]、y[n,1]、y[n,2]表示x[n,:]属于类别0、1、2的概率。这里要注意的是，必须保证概率的和为1，好在我们有softmax函数，做到这点还是没有难度。另外，为了使中间层的数量和输出的维度能够自由修改，我们把二者分别命名为M、K，并将其作为网络的参数(通过输入数据x就能知道N和D的值，所以N和D不在参数里)。
影响网络行为的重要参数——中间层的权重W和输出层的权重V也要传给网络。W是M*(D+1)矩阵(由于还有偏置输入的权重，所以为D+1)，V是K*(M+1)矩阵(这里也需要考虑中间层的偏置神经元，所以为M+1).。
W和V的信息通过汇总了W和V信息的向量wv传递。比如，中间层的神经元数据M=2，输出维度K=3，那么向网络传递的权重为：
W=[[0,1,2],[3,4,5]] M*(D+1)=2*3
V=[[6,7,8],[9,10,11],[12,13,14]] K*(M+1)=3*3
这时的wv为：
wv = np.array([0,1,2,3,4,5,6,7,8,9,10,11,12,13,14])
wv的长度是M*(D+1)+K*(M+1)。将这些参数汇为一个，后面进行最优化的程序就会更容易。
FNN的输出是与N个数据想应的输出y(N*K)矩阵，中间层的输出z，输出层和中间层的输入总和为a,b。
def Sigmoid(x):
y = 1 / (1 + np.exp(-x))
return y
def FNN(wv,M,K,x):
N,D = x.shape #输入维度
w = wv[:M * (D + 1)] #传递到中间层神经元时用到的权重
w = w.reshape(M,(D + 1))
v = wv[M * (D + 1):] #传递到输出层神经元时用到的权重
v = v.reshape((K,M+1))
b = np.zeros((N,M + 1)) #中间层神经元的输入总和
z = np.zeros((N,M+1)) #中间层神经元的输出
a = np.zeros((N,K)) #输出层神经元的输入总和
y = np.zeros((N,K)) #输出层神经元的输出
for n in range(N):
#中间层的计算
for m in range(M):
b[n,m] = np.dot(w[m,:],np.r_[x[n,:],1]) #np.r_[x[n,:],1]将1的虚拟输入作为x的第三个元素加在后面，np.r_[A,B]是横向链接矩阵的命令
z[n,m] = Sigmoid(b[n,m])
#输出层的计算
z[n,M] = 1 #虚拟神经元，求偏置
wkz = 0
for k in range(K):
a[n,k] = np.dot(v[k,:],z[n,:])
wkz = wkz + np.exp(a[n,k]) #softmax函数
for k in range(K):
y[n,k] = np.exp(a[n,k]) / wkz
return y,a,z,b最后测试程序的效果，设M=2，K=3，WV的长度为2*3+3*3=15的权重向量。WV的元素全部为1，输入只使用X_traind两个数据，显示的输出从上到下依次是y，a，z，b的值。
WV=np.ones(15)
M=2
K=3
FNN(WV,M,K,X_train[:2,:]这就是我们神经网络的前向传播，得出来的结果肯定不是我们想要的，参数肯定不是理想的，而要得到理想的参数，就要用到神经网络里面非常重要的误差反向传播。
三、误差反向传播
误差反向传播使用网络输出中的误差(输出与监督信号的差)信息，从输出层权重V到中间层权重W，即与输入反方向地更新权重，这也是这个方法名称的由来。
首先，我们知道每一个输出层的输出后的误差函数是平均交叉熵，那么我们根据平均交叉熵使用梯度法，自然而然就更新了权重。
平均交叉熵：
N是样本数量，K是样本的类别个数。
那要用到梯度法，那我们肯定就离不开平均交叉熵的导数了。
我们先来求离输出层最近的参数V的导数。
我们知道，所以有：
由于过程复杂，我们直接给出结果(对过程有兴趣的可以私信我)。
所以由梯度法就有：
同理离输出层次远的参数W更新如下：
其中
接下来就是代码实现部分了。
首先我们肯定得将平均交叉熵误差函数写出来da
def CE_FNN(wv,M,K,x,t):
N,D = x.shape
y,a,z,b = FNN(wv,M,K,x)
ce = -np.dot(t.reshape(-1),np.log(y.reshape(-1))) / N
return ce接着我们将导数写出来
def dCE_FNN(wv,M,K,x,t):
N,D = x.shape
#把wv恢复为w和v
w = wv[:M * (D + 1)]
w = w.reshape(M,(D + 1))
v = wv[M * (D + 1):]
v = v.reshape((K,M + 1))
#输入x，得到y
y,a,z,b = FNN(wv,M,K,x)
dwv = np.zeros_like(wv)
dw = np.zeros((M,D + 1))
dv = np.zeros((K,M + 1))
delta1 = np.zeros(M) #第一层的误差
delta2 = np.zeros(K) #第二层的误差
for n in range(N):
#求输出层的误差
for k in range(K):
delta2[k] = (y[n,k] - t[n,k])
#求中间层的误差
for j in range(M):
delta1[j] = z[n,j] * (1 - z[n,j]) * np.dot(v[:,j],delta2)
#求v的梯度dv
for k in range(K):
dv[k,:] = dv[k,:] + delta2[k] * z[n,:] / N
#求w的梯度dw
for j in range(M):
dw[j,:] = dw[j,:] + delta1[j] * np.r_[x[n,:],1] / N
#汇总dw和dv的信息，形成dwv
dwv = np.c_[dw.reshape((1,M * (D + 1))),dv.reshape((1,K * (M + 1)))]
dwv = dwv.reshape(-1)
return dwv
下一步，我们用梯度法更新参数
def Fit_FNN(wv_init,M,K,x_train,t_train,x_test,t_test,n,alpha):
wv = wv_init.copy()
err_train = np.zeros(n)
err_test = np.zeros(n)
wv_hist = np.zeros((n,len(wv_init)))
for i in range(n):
wv = wv - alpha * dCE_FNN(wv,M,K,x_train,t_train)
err_train[i] = CE_FNN(wv,M,K,x_train,t_train)
err_test[i] = CE_FNN(wv,M,K,x_test,t_test)
wv_hist[i,:] = wv
return wv,wv_hist,err_train,err_test
接下来，让我们通过作图来看看效果。
M = 2
K = 3
np.random.seed(1)
WV_init = np.random.normal(0,0.01,M*3+K*(M+1))
N_step = 1000
alpha = 0.5
WV,WV_hist,Err_train,Err_test = Fit_FNN(WV_init,M,K,X_train,T_train,X_test,T_test,N_step,alpha)
#显示权重随时间的变化
plt.subplot(1,2,1)
plt.plot(WV_hist[:,:M*3],'r')
plt.plot(WV_hist[:,M*3:],'b')
#显示决策边界
plt.subplot(1,2,2)
Show_data(X_test,T_test)
xb = np.linspace(-2,2,50)
x11 = -(WV[0]*xb + WV[2])/ WV[1]
x12 = -(WV[3]*xb + WV[5])/ WV[4]
x13 = -(WV[6]*xb + WV[8])/ WV[7]
plt.plot(xb,x11,'g')
plt.plot(xb,x12,'r')
plt.plot(xb,x13,'b')
plt.show()
，这样我们结合前馈加反向传播误差就将一个完整的二层神经网络完成了，但是这样实在太过于复杂，于是就有大佬将神经网络做成了一个工具包，我们直接用就可以了。接下来就是用工具keras完成这个二层神经网络的搭建。
四、使用Keras实现神经网络模型
首先，我们先导入我们要的工具包
import numpy as np
import matplotlib.pyplot as plt
import keras.optimizers
from keras.models import Sequential
from keras.layers.core import Dense,Activation接着使用我们原本的数据
np.random.seed(seed=1)
N = 200
K = 3
T = np.zeros((N,3),dtype=np.uint8)
X = np.zeros((N,2))
X_range0 = [-3,3]
X_range1 = [-3,3]
Mu = np.array([[-.5,-.5],[.5,1.0],[1,-.5]])
Sig = np.array([[.7,.7],[.8,.3],[.3,.8]])
Pi = np.array([0.4,0.8,1])
for n in range(N):
wk = np.random.rand()
for k in range(K):
if wk < Pi[k]:
T[n, k] = 1
break
for k in range(2):
X[n,k] = np.random.randn() * Sig[T[n,:] == 1,k] + Mu[T[n,:] == 1,k]
TrainingRatio = 0.5
X_n_training = int(N * TrainingRatio)
X_train = X[:X_n_training,:]
X_test = X[X_n_training:,:]
T_train = T[:X_n_training,:]
T_test = T[X_n_training:,:]然后就是我们的主题，用Keras搭建上诉的二层神经网络模型，并完成训练。
model = Sequential()
#创建model，它是Sequential类型的网络模型，这个model不是变量，而是使用Sequential类生成的对象。
#对象可以看作是几个变量和函数的集合
#Keras通过model中增加层的方式定义网络模型
model.add(Dense(2,input_dim=2,activation='sigmoid',kernel_initializer='uniform'))
#首先，向这个model添加全连接层Dense作为中间层
#Dense()的第一个参数的值是神经元数量
#input_dim=2的意思是输入的维度为2
#activation='sigmoid'的意思是激活函数为Sigmoid函数
#kernel_initializer='uniform'的意思是，权重参数的初始值由均匀随机数决定
#虚拟输入为默认值
model.add(Dense(3,activation='softmax',kernel_initializer='uniform'))
#与上述意义相同
sgd = keras.optimizers.SGD(learning_rate=0.5,momentum=0.0,decay=0.0,nesterov=False)
#定义学习方法
#learning_rate是学习率
model.compile(optimizer=sgd,loss='categorical_crossentropy',metrics=['accuracy'])
#将sgd传给model.compile()，以设置训练方法
#loss='categorical_crossentropy'是将交叉熵误差作为损失函数
#metrics=['accuracy']的意思是同时计算处用于评估学习结果的准确率
history=model.fit(X_train,T_train,epochs=1000,batch_size=100,verbose=0,validation_batch_size=(X_test,T_test))
#X_train,T_train用于指定训练数据
#batch_size=100是一次迭代的梯度计算中使用的训练数据的数量
#epochs=1000是训练时所有数据被使用的次数
#verbose=0的意思是不显示训练进度
#validation_batch_size=(X_test,T_test)用于指定评估用的数据
score = model.evaluate(X_test,T_test,verbose=0)
#输出最终的训练的评估值
#score[0]是测试数据的交叉熵的误差
#score[1]是测试数据的准确率
print('cross entropy {0:.2f},accuracy {1:.2f}'.format(score[0],score[1]))
#输出，所有这里判断训练的效果好坏，不在使用数据可视化，直接看误差和准确率就可以了，到这里我要分享的内容就完了，有什么错误或没明白的地方还望指出(●'◡'●)。
五、文章代码合集
import numpy as np
import matplotlib.pyplot as plt
import keras.optimizers
from keras.models import Sequential
from keras.layers.core import Dense,Activation
np.random.seed(seed=1)
N = 200
K = 3
T = np.zeros((N,3),dtype=np.uint8)
X = np.zeros((N,2))
X_range0 = [-3,3]
X_range1 = [-3,3]
Mu = np.array([[-.5,-.5],[.5,1.0],[1,-.5]])
Sig = np.array([[.7,.7],[.8,.3],[.3,.8]])
Pi = np.array([0.4,0.8,1])
for n in range(N):
wk = np.random.rand()
for k in range(K):
if wk < Pi[k]:
T[n, k] = 1
break
for k in range(2):
X[n,k] = np.random.randn() * Sig[T[n,:] == 1,k] + Mu[T[n,:] == 1,k]
TrainingRatio = 0.5
X_n_training = int(N * TrainingRatio)
X_train = X[:X_n_training,:]
X_test = X[X_n_training:,:]
T_train = T[:X_n_training,:]
T_test = T[X_n_training:,:]
np.savez('class_data.npz',X_train=X_train,T_train=T_train,X_test=X_test,T_test=T_test,X_range0=X_range0,X_range1=X_range1)
def Show_data(x,t):
wk,n = t.shape
for i in range(n):
plt.plot(x[t[:,i] == 1,0],x[t[:,i] == 1,1],marker='o',linestyle='none',alpha=0.8)
plt.grid(True)
plt.subplot(1,2,1)
Show_data(X_train,T_train)
plt.xlim(X_range0)
plt.ylim(X_range1)
plt.title('Training Data')
plt.subplot(1,2,2)
Show_data(X_test,T_test)
plt.xlim(X_range0)
plt.ylim(X_range1)
plt.title('Test Data')
plt.show()
def Sigmoid(x):
y = 1 / (1 + np.exp(-x))
return y
def FNN(wv,M,K,x):
N,D = x.shape
w = wv[:M * (D + 1)]
w = w.reshape(M,(D + 1))
v = wv[M * (D + 1):]
v = v.reshape((K,M+1))
b = np.zeros((N,M + 1))
z = np.zeros((N,M+1))
a = np.zeros((N,K))
y = np.zeros((N,K))
for n in range(N):
for m in range(M):
b[n,m] = np.dot(w[m,:],np.r_[x[n,:],1])
z[n,m] = Sigmoid(b[n,m])
z[n,M] = 1
wkz = 0
for k in range(K):
a[n,k] = np.dot(v[k,:],z[n,:])
wkz = wkz + np.exp(a[n,k])
for k in range(K):
y[n,k] = np.exp(a[n,k]) / wkz
return y,a,z,b
def CE_FNN(wv,M,K,x,t):
N,D = x.shape
y,a,z,b = FNN(wv,M,K,x)
ce = -np.dot(t.reshape(-1),np.log(y.reshape(-1))) / N
return ce
def dCE_FNN(wv,M,K,x,t):
N,D = x.shape
w = wv[:M * (D + 1)]
w = w.reshape(M,(D + 1))
v = wv[M * (D + 1):]
v = v.reshape((K,M + 1))
y,a,z,b = FNN(wv,M,K,x)
dwv = np.zeros_like(wv)
dw = np.zeros((M,D + 1))
dv = np.zeros((K,M + 1))
delta1 = np.zeros(M)
delta2 = np.zeros(K)
for n in range(N):
for k in range(K):
delta2[k] = (y[n,k] - t[n,k])
for j in range(M):
delta1[j] = z[n,j] * (1 - z[n,j]) * np.dot(v[:,j],delta2)
for k in range(K):
dv[k,:] = dv[k,:] + delta2[k] * z[n,:] / N
for j in range(M):
dw[j,:] = dw[j,:] + delta1[j] * np.r_[x[n,:],1] / N
dwv = np.c_[dw.reshape((1,M * (D + 1))),dv.reshape((1,K * (M + 1)))]
dwv = dwv.reshape(-1)
return dwv
def Fit_FNN(wv_init,M,K,x_train,t_train,x_test,t_test,n,alpha):
wv = wv_init.copy()
err_train = np.zeros(n)
err_test = np.zeros(n)
wv_hist = np.zeros((n,len(wv_init)))
for i in range(n):
wv = wv - alpha * dCE_FNN(wv,M,K,x_train,t_train)
err_train[i] = CE_FNN(wv,M,K,x_train,t_train)
err_test[i] = CE_FNN(wv,M,K,x_test,t_test)
wv_hist[i,:] = wv
return wv,wv_hist,err_train,err_test
M = 2
K = 3
np.random.seed(1)
WV_init = np.random.normal(0,0.01,M*3+K*(M+1))
N_step = 1000
alpha = 0.5
WV,WV_hist,Err_train,Err_test = Fit_FNN(WV_init,M,K,X_train,T_train,X_test,T_test,N_step,alpha)
"""
#显示权重随时间的变化
plt.subplot(1,2,1)
plt.plot(WV_hist[:,:M*3],'r')
plt.plot(WV_hist[:,M*3:],'b')
#显示决策边界
plt.subplot(1,2,2)
Show_data(X_test,T_test)
xb = np.linspace(-2,2,50)
x11 = -(WV[0]*xb + WV[2])/ WV[1]
x12 = -(WV[3]*xb + WV[5])/ WV[4]
x13 = -(WV[6]*xb + WV[8])/ WV[7]
plt.plot(xb,x11,'g')
plt.plot(xb,x12,'r')
plt.plot(xb,x13,'b')
plt.show()
"""
model = Sequential()
model.add(Dense(2,input_dim=2,activation='sigmoid',kernel_initializer='uniform'))
model.add(Dense(3,activation='softmax',kernel_initializer='uniform'))
sgd = keras.optimizers.SGD(learning_rate=0.5,momentum=0.0,decay=0.0,nesterov=False)
model.compile(optimizer=sgd,loss='categorical_crossentropy',metrics=['accuracy'])
history = model.fit(X_train,T_train,epochs=1000,batch_size=100,verbose=0,validation_batch_size=(X_test,T_test))
score = model.evaluate(X_test,T_test,verbose=0)
print('cross entropy {0:.2f},accuracy {1:.2f}'.format(score[0],score[1]))