Normalized Wasserstein for Mixture Distributions with Applications in Adversarial Learning and DA

带$\ast$部分暂未填充
混合分布的归一化Wasserstein在对抗性学习和领域适应中的应用

Abstract

• 分布之间适当的距离测量是一些学习任务的核心，如生成模型、领域适应、聚类等。
• 本文专注于混合分布，这种分布在几个应用领域中自然产生，其中数据包含不同的子群体。
  Existing Problem:
• 对于混合分布，已有的距离测量方法，如Wasserstein距离，没有考虑到不平衡的混合比例。
• 因此，即使两个混合分布具有相同的混合物成分，但混合比例不同，它们之间的Wasserstein距离也会很大。这往往会导致基于距离的混合分布学习方法出现不理想的结果。
  Proposed Method
• 引入归一化Wasserstein度量来解决这个问题。其关键思想是引入混合比例作为优化变量，有效地将Wasserstein公式中的混合比例规范化。
• 与普通的Wasserstein距离相比，使用所提出的归一化Wasserstein度量对于具有不平衡的混合比例的混合分布有明显的性能提升。
• 在几个基准数据集中证明了所提措施在GANs、领域适应和对抗性聚类中的有效性

Introduction

  量化概率分布之间的距离是机器学习和统计中的一个基本问题，在生成模型、领域自适应、聚类等方面有多个应用。流行的概率距离度量包括最优运输度量，如瓦瑟斯坦距离和散度度量，如库尔贝克-莱布勒(KL)散度。

  然而，经典的距离度量可能会导致混合分布的一些问题。混合分布是一个随机变量X的概率分布，其中$X=X_i$的概率${\pi }_i$为$1\le i\le k$。$k$是混合成分的数量，${\pi =[\pi 1，...，\pi k]}^T$是混合（或模式）比例的向量。每个$X_i$的概率分布被称为一种混合成分（或，一种模式）。混合分布自然地出现在不同的应用程序中，其中数据包含两个或更多的子种群。例如，具有不同标签的图像数据集可以被视为一种混合（或多模态）分布，其中具有相同标签的样本表征了一个特定的混合成分。

  如果两个混合分布具有完全相同的混合成分(即相同的$X_i$)，且具有不同的混合比例（即不同的$\pi$），那么两者之间的经典距离度量将会很大。这可能会在一些基于远程的机器学习方法中导致不希望出现的结果。为了说明这个问题，考虑两个分布$P_X$和$P_Y$之间的瓦瑟斯坦距离，定义为:

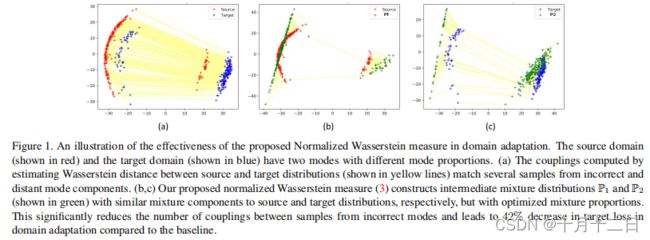
  瓦瑟斯坦距离优化是针对所有的联合分布（耦合）$P_{X,Y}$，其边际分布与输入分布$P_X$和$P_Y$完全匹配。当$P_X$和$P_Y$是具有不同混合比例的混合分布时，这一要求可能会引起问题。在这种情况下，由于边际约束，属于非常不同的混合组分的样品必须在$P_{X,Y}$中耦合在一起(e.g. Figure 1(a))。因此，使用这种距离度量可能会在领域适应等问题上导致不良的结果。这促使人们需要开发一种新的距离度量，以考虑到混合分布中的模式不平衡。

  本文提出了一种新的距离度量方法，解决了多模态分布的不平衡混合比例的问题。发展集中在一类最优运输措施，即瓦瑟斯坦距离方程（1）。然而，想法也可以很自然地扩展到其他的距离度量（例如，对抗性的距离）。

设G是一个生成器函数的数组，其中$k$个分量定义为$G：=[G_1，...，G_k]$。设$P_{G，\pi }$为随机变量$X$的混合概率分布，其中$X=G_i(Z)$的概率为${\pi }_i$，$1\le i\le k$。在本文中，假设$Z$具有正态分布。通过放宽经典瓦瑟斯坦距离（1）的边际约束，我们引入了归一化瓦瑟斯坦测度(NW测度)如下：

  在这个定义中有两个关键思想有助于解决混合分布的模式不平衡问题。首先，我们没有直接测量$P_X$和$P_Y$之间的瓦瑟斯坦距离，而是构建了两个中间（和潜在的混合）分布，即$P_{G,{\pi }^{(1)}}$和$P_{G,{\pi }^{(2)}}$。这两种分布具有相同的混合组分(即相同的G)，但可以有不同的混合比例（即${\pi }^{(1)}$和${\pi }^{(2)}$可以不同）。其次，将混合比例、${\pi }^{(1)}$和${\pi }^{(2)}$作为优化变量。这在瓦瑟斯坦距离计算之前有效地标准化了混合比例。参见Figure 1 (b, c)中的示例，可视化$P_{G,{\pi }^{(1)}}$和$P_{G,{\pi }^{(2)}}$以及重新规范化步骤。

  在本文中，证明了所提出的标准化沃瑟斯坦度量在三个应用领域的有效性。在每种情况下，当输入数据集是混合比例不平衡的混合分布时，我们提出的方法的性能比基线显著提高。将简要地强调这些结果：

• 域适应：将域适应问题表述为最小化源特征分布和目标特征分布之间的归一化瓦瑟斯坦度量。在不平衡数据集的分类任务上，我们的方法显著优于基线(例如，∼在VISDA-3数据集上合成到真实适应的20%增益)。
• GANs：使用GAN公式中的归一化沃瑟斯坦测度来训练具有不同模式比例的混合模型。我们表明，这样的生成模型可以帮助捕获罕见的模式，降低生成器的复杂性，并重新规范化一个不平衡的数据集。
• 对抗性聚类：使用归一化瓦瑟斯坦测度将聚类问题表述为一个对抗性学习任务。

Normalized Wasserstein Measure

  G是一个定义为$G：=[G_1,...,G_k]$，其中$G_i：R^r\to R^d$。设$\mathcal{G}$是所有可能的G函数数组的集合。设π是一个具有k个元素的离散概率质量函数，即$\pi =[{\pi }_1,{\pi }_2,\cdot \cdot \cdot ,{\pi }_k]$，其中${\pi }_i\ge 0$,${\sum }_i^{}{\pi }_i=1$。设Π是所有可能的$\pi$的集合。
  设$P_{G,\pi }$是一个混合分布，即它是一个随机变量$X$的概率分布，使$X=G_i(Z)$的概率为$\pi i$。我们假设$Z$有一个正常的密度，即$Z\sim N(0，I)$。我们将$G$和$\pi$分别称为混合成分分和比例(mixture components and proportions)。所有这些混合物分布的集合被定义为：

  其中，$k$为混合成分的个数。给定两个分布$P_X$和$P_Y$属于混合分布族$P_{G,k}$，我们感兴趣的是定义一个距离测量，与模式比例的差异无关，但对模态成分（ components）的变化很敏感，即只有当$P_X$和$P_Y$的模态成分（ components）不同时，距离函数才应具有较高的值。如果$P_X$和$P_Y$具有相同的模分量，但仅模态比例不同，则距离应较低。
  其主要思想是在瓦瑟斯坦距离公式（1）中引入混合比例作为优化变量。这导致了以下距离度量，我们称之为归一化沃瑟斯坦度量（NW度量），$W_N(P_X,P_Y)$，定义为：

   自规范化瓦瑟斯坦的优化（3）包括混合比例${\pi }^{(1)}$和${\pi }^{(2)}$优化变量，如果两个混合分布有类似的混合组件与不同的混合比例(即$P_X=P_{G,{\pi }^{(1)}}$和$P_Y=P_{G,{\pi }^{(2)}}$，尽管两者之间的瓦瑟斯坦距离可以很大，引入规范化瓦瑟斯坦测量两者之间将为零。请注意，WN是根据一组生成器函数G=[G_1,…,G_k]来定义的。但是，为了简化符号，本文将这种依赖项隐式。本文想指出，我们提出的NW度量是一个半距离度量（而不是一个距离），因为它不满足一个距离度量的所有性质。
   为了计算NW测度，我们使用了一种类似于双重计算瓦瑟斯坦距离的交替梯度下降方法。此外，我们使用一个软最大函数来施加π约束。

Normalized Wasserstein in Domain Adaptation

  演示了NW度量在无监督域适应(UDA)中的有效性，无论是有监督（如分类）还是无监督（如去噪）任务。请注意，UDA中的无监督术语意味着目标域中的标签信息是未知的，而无监督任务意味着源域中的标签信息是未知的。
  首先，我们考虑了一个分类任务的领域自适应。$(X_s,Y_s)$表示源域，$(X_t,Y_t)$表示目标域。由于处理分类设置，我们有$Y_s,Y_t\in \{1,2，...，k\}$。域自适应问题的一个常见公式是将$X_s$和$X_t$转换为一个特征空间，其中源特征分布和目标特征分布之间的距离足够小，而在该空间中对源域可以计算出一个很好的分类器。在这种情况下，我们可以解决以下优化问题：

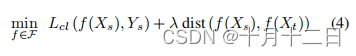
其中，$\lambda$是一个自适应参数，$L_{cl}$是经验分类损失函数（例如，交叉熵损失）。分布之间的距离函数可以是对抗性距离，瓦瑟斯坦距离，或基于MMD的距离。
  当$X_s$和$X_t$是具有不同混合比例的混合分布（通常是每个标签对应一个混合分量）时，使用这些经典的距离度量可能会导致计算不适当的变换和分类函数。在这种情况下，我们建议使用NW测度作为距离函数。计算NW度量需要训练混合分量G和模式比例${\pi }^{(1)}$和${\pi }^{(2)}$。为了简化计算，我们利用了源域(即$Y_s$)的标签是已知的这一事实，因此可以使用这些标签来识别源混合成分。利用这些信息，我们可以避免直接计算G，并使用条件源特征分布作为混合成分的代理，如下所示：

上述公式可以看作是实例加权的一个版本，因为${X_s}^{(i)}$中的源样本由${\pi }_i$加权。域自适应的实例加权机制已经得到了充分的研究。然而，与这些方法不同的是，我们使用神经网络以端到端方式训练模式比例向量$\pi$，并将实例权重集成到瓦瑟斯坦优化中。与我们的工作更相关的是在[3]中提出的方法，其中实例加权是在神经网络中端到端训练的。然而，在[3]中，实例权值相对于瓦瑟斯坦损失是最大，而我们表明混合比例需要最小化来归一化模式不匹配。此外，我们的NW测度公式可以处理源嵌入的模式分配未知的情况（正如我们在第4.2节中讨论的）。这种情况不能用[3]中提出的方法来处理。
  对于当源样本的模式分配未知时的无监督任务，我们不能使用（5）的简化公式。在这种情况下，我们使用一种领域自适应方法来求解以下优化：

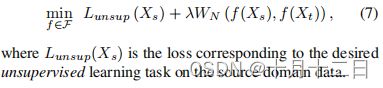
UDA for supervised tasks*

MNIST → MNIST-M*

VISDA*

Mode balanced datasets*

UDA for unsupervised tasks*

Normalized Wasserstein GAN*

Mixture of Gaussians*

A Mixture of CIFAR-10 and CelebA*

Adversarial Clustering*

Choosing the number of modes*

Conclusion

  在本文中，我们证明了瓦瑟斯坦距离由于其边际约束，当应用于不平衡混合分布时会导致不期望的结果。为了解决这个问题，我们提出了一种新的距离度量，称为标准化瓦瑟斯坦。其关键思想是在距离计算中优化混合比例，有效地归一化混合不平衡。我们演示了NW度量在三个机器学习任务中的有效性：GANs、领域自适应和对抗性聚类。对这三个问题的强实证结果突出了所提出的距离度量的有效性

论文链接
[3] Qingchao Chen, Yang Liu, Zhaowen Wang, Ian Wassell, and Kevin Chetty. Re-weighted adversarial adaptation network for unsupervised domain adaptation. In The IEEE Conference on Computer Vision and Pattern Recognition (CVPR),June 2018.