数字图像处理——第五章图像复原与重建

5.1 绪论

当图像中具有加性噪声和周期噪声时，图像就会发生退化，我们可以利用噪声的不同特点，选取空间域和频率域的滤波器对图像进行复原，目的使设立一个最佳准则产生期望结果得最佳估计，使复原后得图像尽可能接近原图像。

5.2 图像退化/复原过程的模型

退化的过程可建模原图像经过退化函数H和加性噪声项$\eta$，通过一个复原滤波器得到估计图像函数$\hat{f}$(x,y)，也表示为g(x,y)。
模型如下图：

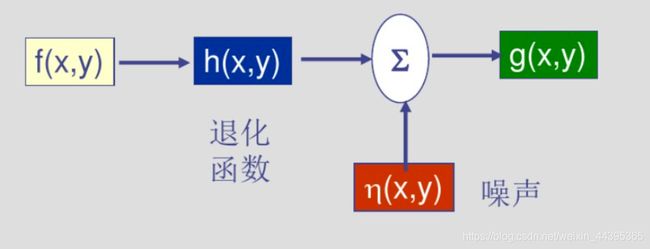
g(x,y)=h(x,y)★f(x,y)+$\eta$(x,y)，星号表示空间卷积，在频率域中，G(u,v)=H(u,v)F(u,v)+N(u,v)。

5.2.1 常见噪声概率密度函数

高斯噪声：概率密度函数呈正态分布，当均值为0，方差为1时也被称为白噪声
瑞丽噪声
爱尔兰（伽马）噪声
指数噪声
均匀噪声
脉冲（椒盐）噪声

我们这里介绍高斯噪声和椒盐噪声的概率密度函数和分布图。
高斯的PDF函数：$$p(z)=\frac{1}{\sqrt{2\pi }\sigma }{e}^{\frac{-(z-\mu {)}^2}{2{\sigma }^2}}，z是灰度值，\mu 是均值，\sigma 是标准差$$
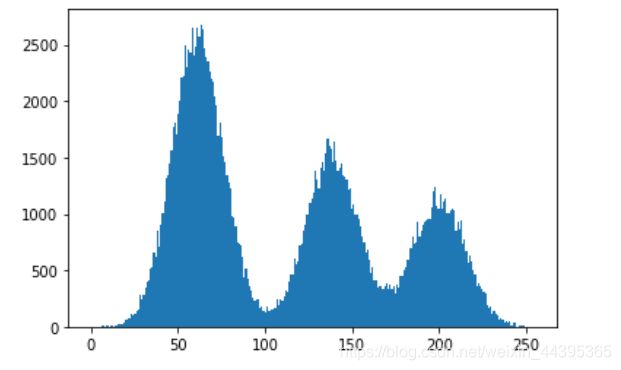
服从正态分布，分布图像如下：

椒盐噪声也叫做脉冲噪声，在图像退化中看起来是许多灰度值相同的点污染了图像，椒盐噪声分为胡椒噪声和盐粒噪声，其中盐粒噪声的灰度值较大。
PDF函数：

分布图像：
如同所示，它的分布特点是双极分布。
我们可以给图像加入高斯和椒盐噪声，并观察直方图。

#高斯噪声
def add_GaussNoise(image, mean=0, var=0.025):
    
    image = np.array(image/255, np.float32)                    
    noise = np.random.normal(mean, var, image.shape)    
    out = image + noise                                     
    
    if out.min() < 0 or out.min()==0:
        low_clip = -1.
    #截断函数
    out = np.clip(out, low_clip, 1.0)
    #恢复到原灰度范围
    out = np.uint8(out*255)
    return out

def addsaltpepper(img,SNR):
    mask=np.zeros(img.shape,np.uint8)
    print(mask.shape)
    thres=1-SNR
    for i in range(0,img.shape[0]):
        for j in range(0,img.shape[1]):
            k=random.random()
            if k<SNR:
                mask[i][j]=img[i][j]=0
            elif k>thres:
                mask[i][j]=img[i][j]=255
            else:
                mask[i][j]=img[i][j]
    return mask

Gauss分布：

saltpepper分布：

5.2.2 周期噪声

周期噪声是在图像获取期间由电力或机电干扰产生的，周期噪声可通过频率域滤波来显著得减少，我们知道周期噪声如果是正弦函数，那么在频率域得频谱中就会呈现一对共轭脉冲，我们只要添加上对称的陷波滤波器，图像复原的效果是很好的。

img=cv.imread('pic/contaminated by sin waves.tif',0)
float_img=np.float32(img)
DFT_img = cv.dft(float_img, flags=cv.DFT_COMPLEX_OUTPUT)

DFT_center_img = np.fft.fftshift(DFT_img) 
# 将两个通道放大
DFT_center_img1 = 20 * np.log(cv.magnitude(DFT_center_img[:, :, 0],DFT_center_img[:, :, 1]))
plt.subplot(121),show(img),plt.title('original image')
plt.subplot(122),show(DFT_center_img1),plt.title('spectrum')
plt.show()

冲击共轭分布：

5.3 空间滤波

我们用滤波器，也称kernel来处理像素领域的值，滤波器的种类和大小都会对图像复原产生影响。

• 算术均值滤波器：$$\hat{f}(x,y)=\frac{1}{mn}\sum _{(s,t)\in S_{xy}}g(s,t)$$
  属于平滑滤波器，降低噪声，模糊图像，适合处理高斯或均匀随机噪声

• 几何均值滤波器：$$\hat{f}(x,y)=[\prod _{(s,t)\in S_{xy}}g(s,t){]}^{\frac{1}{mn}}$$
  与算术均值滤波器相比，丢失的图像细节较少。

• 谐波均值滤波器：$$\hat{f}(x,y)=\frac{mn}{{\sum }_{(s,t)\in S_{xy}}\frac{1}{g(s,t)}}$$
  擅长处理盐粒和高斯噪声

• 逆谐波均值滤波器：$$\hat{f}(x,y)=\frac{1}{mn}\sum _{(s,t)\in S_{xy}}\frac{g(s,t{)}^{Q+1}}{g(s,t{)}^Q}$$
  Q称为滤波器的阶数，Q>0，用来消除胡椒噪声，Q<0，用来消除盐粒噪声。

• 中值滤波器：适用于处理单极或双脉冲噪声

• 最值滤波器：发现图像中最暗/亮的点

• 自适应滤波器：

有4个参数：噪声和图像的灰度值，图像和噪声的方差
若两个方差高度相关，则返回噪声灰度值的近似值，若方差相等，则返回图像中相关区域的算术均值。

5.3.1 空间域滤波实验

我主要做了关于均值滤波的实验。

#实验一算术均值滤波器
def suanshu_mean(img,kernel_size):
    G_mean_img=np.zeros(img.shape)
    k=int((kernel_size-1)/2)
    for i in range(0,img.shape[0]):
        for j in range(0,img.shape[1]):
             if i <k or i>(img.shape[0]-k) or j <k or j>(img.shape[1]-k):
                            G_mean_img[i][j]=img[i][j]
             else:
                for n in range(1,kernel_size):
                    for m in range(1,kernel_size):
                        G_mean_img[i][j] +=np.int32([1/(kernel_size*kernel_size)]*img[i-k+n-1][j-k+m-1])
    G_mean_img = np.uint8(G_mean_img)
    return G_mean_img
img04=suanshu_mean(img01,kernel_size=3)
plt.subplot(121),plt.imshow(img01),plt.title('contaminated by gauss')
plt.subplot(122),plt.imshow(img04),plt.title('suanshu filter')
plt.show()

结果如下：平滑图像且消除了高斯噪声

#实验二几何均值滤波器
def jihe_mean(img,kernel_size):
 
    G_mean_img = np.ones(img.shape)
  
    k = int((kernel_size-1)/2)
    #print(k)
    for i in range(img.shape[0]):
        for j in range(img.shape[1]):
             if i <k or i>(img.shape[0]-k-1) or j <k or j>(img.shape[1]-k-1):
                            G_mean_img[i][j]=img[i][j]
             else:
                for n in range(1,kernel_size):
                    for m in range(1,kernel_size):
                               
                                G_mean_img[i][j]*=(img[i-k+n-1][j-k+m-1])
                               
    G_mean_img[i][j] = G_mean_img[i][j]**[1/(kernel_size*kernel_size)]
                                
    G_mean_img =np.uint8(G_mean_img)
    

    return G_mean_img

img05=jihe_mean(img01,2)
plt.subplot(121),plt.imshow(img01),plt.title('contaminated by gauss')
plt.subplot(122),plt.imshow(img05),plt.title('jihe filter')
plt.show()

结果如图：比起算术均值滤波器，保留了更多细节，灰度值也更接近原图，效果是十分出色的。

#实验三 谐波均值滤波
def xiebo_mean(img,kernel_size):
    G_mean_img = np.zeros(img.shape)
    k = int((kernel_size-1)/2)
    for i in range(0,img.shape[0]):
        for j in range(0,img.shape[1]):
            if i <k or i>(img.shape[0]-k-1) or j <k or j>(img.shape[1]-k-1):
                G_mean_img[i][j]=img[i][j]
            else:
                for n in range(kernel_size):
                    for m in range(kernel_size):
                        if img[i-k+n-1][j-k+m-1].all() ==0:
                            G_mean_img[i][j] = 0
                            break
                        else:
                            G_mean_img[i][j] +=1/(img[i-k+n-1][j-k+m-1])
                    else:
                        continue
                    break
                if G_mean_img[i][j].all()!=0:
                    G_mean_img[i][j] = (kernel_size*kernel_size)/G_mean_img[i][j]
    G_mean_img = np.uint8(G_mean_img)
    return G_mean_img
img05=xiebo_mean(img02,1)

plt.subplot(121),plt.imshow(img03),plt.title('contaminated by salt')
plt.subplot(122),plt.imshow(img05),plt.title('xiebo filter')
plt.show()

结果如图所示：处理盐粒效果较好，但滤波器不宜大，否则效果不好，3 * 3的滤波器效果很差，我所用的是1*1的

#实验四逆谐波均值滤波器
def re_mean(img,kernel_size,Q):
 
    G_mean_img = np.zeros(img.shape)
    #print(G_mean_img[0][0])
 
    #print(img)
    k = int((kernel_size-1)/2)
    #print(k)
 
    for i in range(img.shape[0]):
        for j in range(img.shape[1]):
            if i <k or i>(img.shape[0]-k-1) or j <k or j>(img.shape[1]-k-1):
                G_mean_img[i][j]=img[i][j]
            else:
                result_top = 0
                result_down = 0
                for n in range(kernel_size):
                    for m in range(kernel_size):
                        if Q>0:
                            result_top +=pow((img[i-k+n-1][j-k+m-1]),Q+1)
                            result_down +=pow((img[i-k+n-1][j-k+m-1]),Q)
                        else:
                            if img[i-k+n-1][j-k+m-1].all()==0:
                                G_mean_img[i][j] = 0
                                break
                            else:
                                result_top +=pow((img[i-k+n-1][j-k+m-1]),Q+1)
                                result_down +=pow((img[i-k+n-1][j-k+m-1]),Q)
                    else:
                        continue
                    break
 
                else:
                    if result_down.all() !=0:
                        G_mean_img[i][j] = result_top/result_down
 
 
                
    G_mean_img = np.uint8(G_mean_img)
    return G_mean_img

img07=re_mean(img02,1,1.5)
img08=re_mean(img03,1,-1.5)

plt.subplot(221),plt.imshow(img02),plt.title('pepper'),plt.xticks([]) 
plt.subplot(222),plt.imshow(img03),plt.title('salt'),plt.xticks([]) 
plt.subplot(223),plt.imshow(img07),plt.title('Q=1.5')
plt.subplot(224),plt.imshow(img08),plt.title('Q=-1.5')
plt.show()

结果如下：Q>0适合处理胡椒噪声，Q<0适合处理盐粒噪声，如果Q的正负出错了会给图像造成灾难性的污染。

5.4 频率域消除周期噪声

5.2.2节中介绍了频率域中周期噪声频谱的特点（假设噪声是正弦信号），即周期复共轭的冲击脉冲，我们根据这一特点，使用带通，带阻和和陷波滤波器均可以达到消除周期噪声的效果，这一节，我会使用带阻滤波器，滤波器的特点在第四章的博客中写过，这里不再重复了。
带阻滤波器通过设置适当的半径和宽度，包围噪声脉冲，我这里使用4阶布特沃斯型的带阻滤波器。表达式如下：$$H(u,v)=\frac{1}{1+[\frac{DW}{D^2-D_0^2}{]}^{2n}}$$
式子得出，离截止频率近，滤波器额值趋于0。
w是带宽，D是D(u,v)距滤波器中心的距离，D${}_0$是截止频率。
基本流程：

import cv2
import numpy as np
import math
from matplotlib import pyplot as plt
img = cv2.imread('pic/contaminated by sin waves.tif',0)
show(img)
def buttworth(img,D0,w):
    img_float32 = np.float32(img)
    dft = cv2.dft(img_float32, flags=cv2.DFT_COMPLEX_OUTPUT)
    dft_shift = np.fft.fftshift(dft)
    rows, cols = img.shape 
    crow, ccol = int(rows / 2), int(cols / 2)  
    buttworth = np.ones((rows, cols,2), np.uint8) 
    for i in range(0, rows): 
        for j in range(0, cols):
            d = math.sqrt(pow(i - crow, 2) + pow(j - ccol, 2)) 
            if D0 - w / 2 < d < D0 + w / 2 and (d*d-D0*D0)!=0:
                buttworth[i,j,0]=buttworth[i,j,1]=(1/(1+(pow(d*w/(d*d-D0*D0),4))))
            else:
                buttworth[i,j,0]=buttworth[i,j,1]=1
    f = dft_shift * buttworth 
    ishift = np.fft.ifftshift(f) 
    iimg = cv2.idft(ishift) 
    res = cv2.magnitude(iimg[:, :, 0], iimg[:, :, 1]) 
    return res
img01=buttworth(img,20,5)
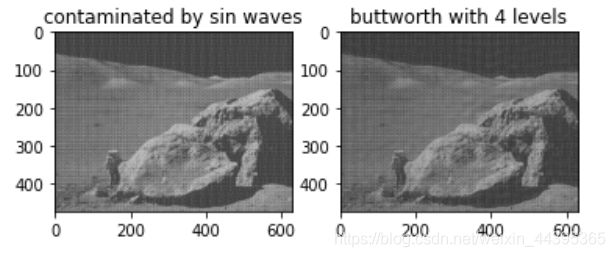
plt.subplot(121),show(img),plt.title('contaminated by sin waves')
plt.subplot(122),show(img01),plt.title('buttworth with 4 levels')
plt.show()

结果如图：肉眼不太好观察，应有一部分周期噪声被滤除

5.5 图像的逆滤波

逆滤波：

要注意退化函数为零或为非常小的情况，一种方法是限制滤波的频率，使其接近原点。
维也纳滤波：

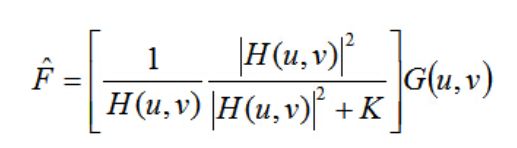
K值的交互式选择是为了找到最好的视觉效果。

总结

本章主要从图像复原的角度介绍了众多噪声模型和滤波器模型，不同滤波器的特点和参数要搞清楚，对于滤波器的模型编码能力要加强。