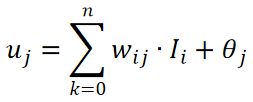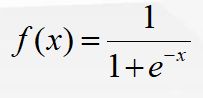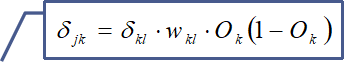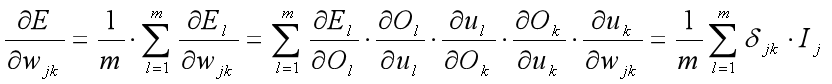matlab使用日记（三）——人工神经网络
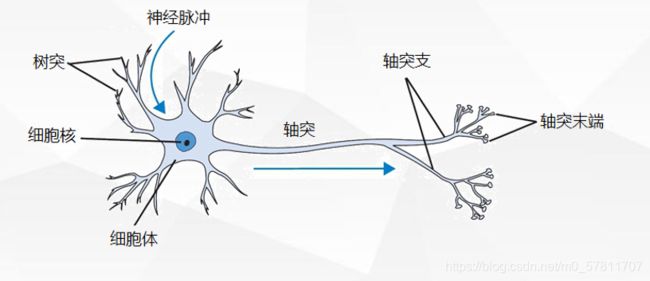
人工神经网络是人们通过模仿神经元的工作原理设计出的模型，旨在指导计算机进行多次学习，然后预测出较为准确的结果。
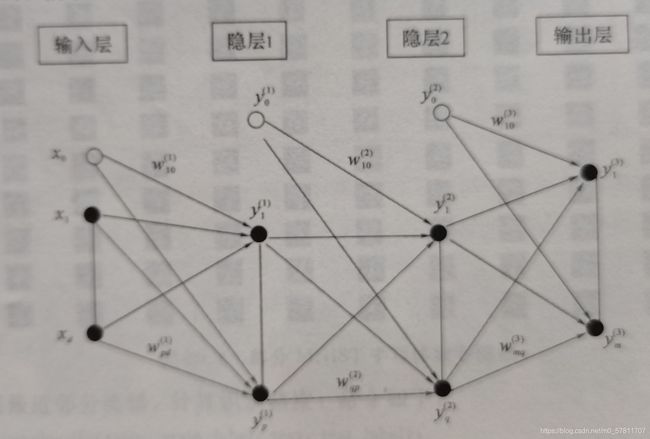
跟神经元类似，人工神经网络结构也是多层结构。依次是输入层，隐藏层，输出层：
输入层：负责接受样本数据中各变量的数值；
隐藏层：负责实现运算与非线性性质；
输出层：负责处理后结果的输出。
下面我们着重了解一下BP（(back propagation，前馈）神经网络。BP神经网络是目前应用最广泛的一种人工神经网络模型，前馈是指信息只会向前方传播，即从输入节点到隐藏节点再到输出节点。整个网络中不存在反馈，可以表示为一个有向无环图。
BP神经网络处理，分为以下几步：
一，初始化网络权值与处理各单元的阈值（一般是随机赋值）；
二，根据组合函数与激活函数逐层计算；
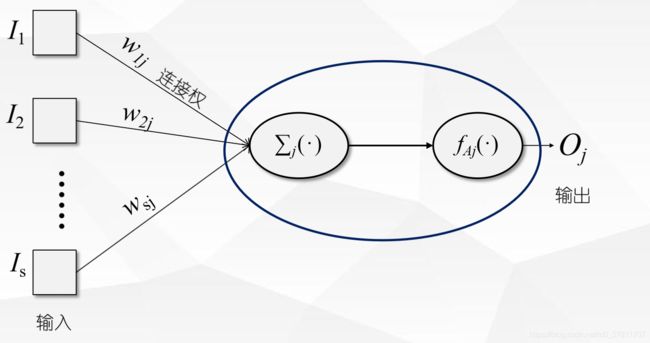
至于激活函数与组合函数，一般指的是将输入转换为输出的中间函数，放在隐藏层中。
组合函数是这样的
指的是输入节点 i 到隐藏层 j 节点的权值， 
指的是我们预设的神经元阈值。
激活函数最常用的是
，
这样的话，神经网络的输出就会是
。
此时，实际输出我们知道是Y[j],与我们得出的O[j]是不同的。此时就要对网络中的权值和阈值进行调整，使神经网络的输出能够逼近Y[j]。
三，误差后向传播
此时可用两种处理方法，梯度下降法与共轭梯度法。
这里讲一下梯度下降法（因为我也只理解了梯度下降法）。
假设我们有一个微分函数，以某个点的所处的位置为基准，寻找这个位置最陡峭的地方，然后朝着下降方向走一步，然后又继续以当前位置为基准，再找最陡峭的地方，再走直到最后到达最低处；
因为梯度是下降最快的地方，所以我们能极其迅速地到达局部最小点处。
回到神经网络，我们对权值求偏微分，梯度下降算法调整权值w[i,j]的大小，就可以使其最小化来降低系统误差。
对于激活函数 而言，求偏微分会得到这样一个公式：
修正阈值：为了控制权值的修正速度，我们加入一个学习率 —— 
（再0~1之间），多次迭代后误差会降低到可以接受的程度；
四，最后对建立完成的模型进行评估与应用，保证误差E小于一个极小值。
接下来我们用matlab实战一下。
matlab实战过程
模板可以参照这位大佬的模板，我也是跟着他的博文写的。
BP神经网络matlab代码讲解与实现步骤_wishes61的博客-CSDN博客_bp神经网络
题目
已知输入向量P和目标向量T，建立一个BP神经网络，找到P和T之间的关系。
P=-1:0.1:1;
T=[-0.96 -0.577 -0.0729 0.377 0.641 0.66 0.461 0.1336 -0.201 -0.434 -0.5 -0.393 -0.1647 0.0988 0.3072 0.396 0.3449 0.1816 -0.0312 -0.2183 -0.3201];
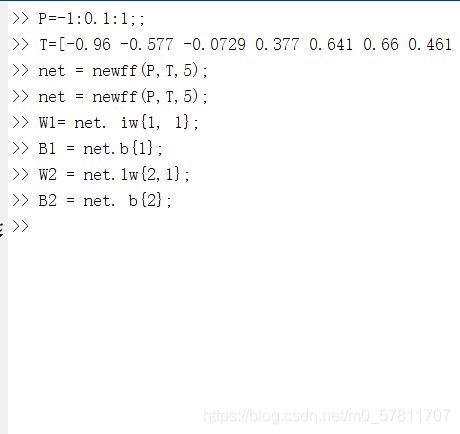
matlab中，有可以直接进行建立一个神经网络的命令。
net = newff（P，T，k）；建立一个名为net的神经网络模型，含有k个隐层节点，默认使用梯度下降法（trainlm）；
输入 中间隐藏层的权值，阈值。W表示权值，B表示阈值。
然后，再给模型规定训练次数，学习速率和最小误差；
下面给一个指令表格，可以保存一下。
| 训练参数名称及默认值 |
属性 |
| net.trainParam.epochs=100 |
最大训练次数 |
| net.trainParam.goal=0 |
训练目标 |
| net.trainParam.show=25 |
两次显示之间的训练次数（无显示时取NAN） |
| net.trainParam.time=inf |
最大训练时间（秒） |
| net.trainParam.max_fail=5 |
确认失败的最大次数 |
| net.trainParam.min_grad=1e-6 |
最小性能梯度 |
| net.trainParam.lr=0.2 |
学习速率 |
所有准备都做好以后，就可以直接开始训练了，训练函数为train(net,P,T);
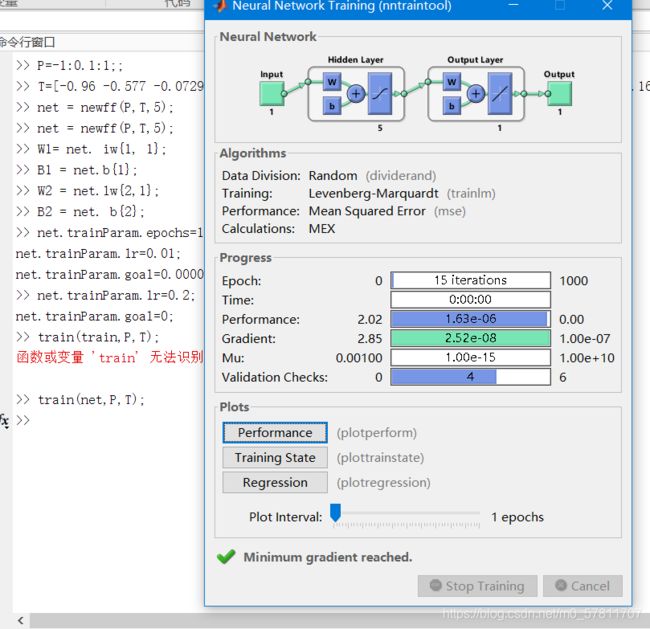
然后就会弹出一个窗口，就像下面一样。
至于这些英文大概是什么意思，我从大佬的文章中找出这样一张图——
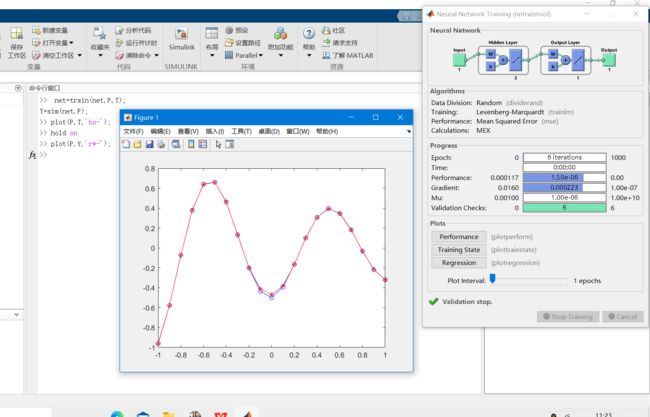
训练完成后就可以进行仿真——Y=sim(net,P);
之后我们把图绘画出来看一看。
可以看到，我们做出的BP神经网络模型在经过训练之后，它与我们所期待的已经很类似了，中间输出的点与实际输入误差也变得比较小了。
好了，人工神经网络先写到这，之后会再更新一次，把评估模型的matlab上传。