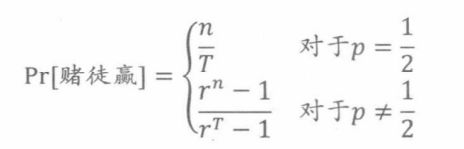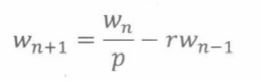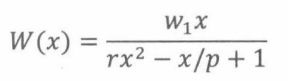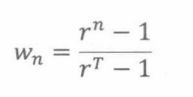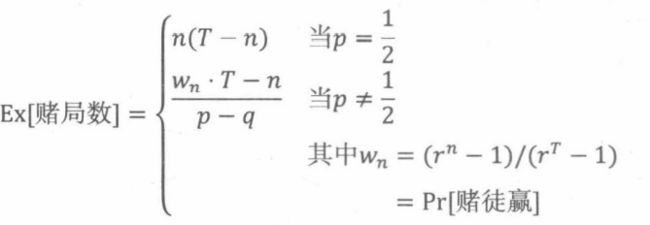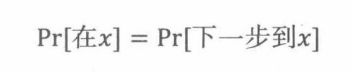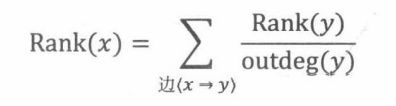第21章 随机游走

第21章 随机游走

随机游走的建模场景是某个对象按照随机选择的方向行走一个步数序列。

21.1赌徒破产

假设一个赌徒一开始有n美元赌注，他要进行一系列1美元投注。如果他赢得一局，则拿回他的赌注外加1美元。如果他输了，那么他将失去1美元。

我们可以将这个场景建模为实线上整数点之间的随机游走。任何时候，线上的位置对应于赌徒手上的现金。赌徒一直下注，直到他没钱了，或者资本增加至目标金额T美元。每一次赌局赢得概率是p，且相互独立，我们想知道资本增加至T美元的概率。

下图描绘了赌徒的1美元赌博情形。随机游走的边界为0和T。

对于无偏博弈，资本增加到T美元的概率取决于你的初始资金和目标T。假设想赢100美元，初始资金是500美元。这时他赢100美元的概率是5/6。如果他以100 万美元开始，目标仍是赢100美元，他概率是1M / (1M＋100) > 0.9999。

但是，对于不公平的博弈，我们就不能按照上面的方法去计算了。

21.1.1避免破产的概率

定理21.1.1：在赌徒破产博弈中，初始资本为n，目标为T，每一局获胜的概率为p,

其中r:= q/p。

21.1.2获胜概率递推

线性递推为这类基本问题提供了一种有条不紊的方法。

赌徒获胜的概率是初始资本n、目标T (T≥n)和每一局获胜概率p(失败的概率为q)的函数。给定p和T令$w_n$是初始资本为n美元时赌徒获胜的概率。

根据全概率公式，他获胜的概率是$w_n=p{W}_{n+1}+q{W}_{n-1}$。求解$w_{n+1}$，得

其中r等于q/p。

假设：

是$w_n$的母函数，使用母函数方法可得：

当p ≠ q时，我们可以解得：

当p = q时，解得：$w_n=n/T$

求得的结果与上一小节中相匹配。

21.1.3 有偏情形的简单解释

有偏博弈中赌徒获胜的概率表达式21.1不太好解释。当赌徒的初始资本很大，游戏对赌徒有不利的偏差时，这个上界更简单、更紧凑。那么r >1，式21.1的分子和分母均为正，分子较小。所以

推论21.1.2在初始资本为n、目标为T、单次获胜概率为p <1/2的赌徒破产博弈中，

其中r::= q/p >1。

为什么游戏对他稍有不公，赌徒就不太可能赚钱?为了直观地回答这个问题，我们考虑赌徒钱包的两种作用力。首先，运气好坏导致赌徒的资本随机上下波动。第二，赌徒的资本将会有一个稳定的向下漂移，因为负面偏差意味着每一局平均损失几美分。情况如图21.2所示。

在公平的比赛中，没有漂移;波动是唯一的影响。在没有向下漂移的情况下，我们前面的直觉是正确的。如果赌徒以万亿美元开始，那么几乎肯定会有一次幸运的摆动，把他的资本提高100美元。

21.1.4步长多长

我们已经知道了赌徒在公平和不公平的游戏（博弈）中获胜的概率wn，现在再来考虑他平均需要多少局才能获得胜利或者破产。线性递推方法在这里也很有用。对于固定的p和T，令en为赌徒从初始资本n美元到游戏结束时的赌局数目。从而得到：

线性递推为：

从以上线性递推可以得到如下定理。
定理21.1.3：在初始资产为n，目标为T，每一局获胜概率为p的赌徒破产博弈中，

在无偏情况下，上式可以简写成

21.1.5赢了就退出

假设赌徒永远不会赢了就跑。也就是说，他以n >0美元开始，不管任何目标T，他都直玩到彻底破产，这称为无限赌徒破产博弈。

引理21.1.4 如果赌徒以1美元或更多钱开始，进行无限赌徒破产博弈，那么他将以概率1破产。

我们知道在一场公平的比赛中，他输的概率是1- n/T。如果选择足够大的T，这个数字可以任意接近1。因此，在没有任何目标的情况下，他失败的概率有一个任意接近1的下限所以实际上一定是1。

引理21.1.5如果赌徒以1美元或更多钱开始进行无限公平博弈，那么他能玩的预期次数是无限的。

21.2图的随机游走

万维网的超链接结构可以用有向图来表示。顶点表示网页，如果网页x有一个指向网页y的超链接，则存在一条从顶点x到顶点y的有向边。

21.2.1网页排名初探

考虑网页图，我们在搜索引擎中搜索，你认为哪个顶点（或网页）应该排在第一名?

将x的网页排名( page rank)定义为indegree(x)，即指向x的链接数。这一想法将网页链接看成重要性投票—网页得票越多它越重要。

不幸的是，这个想法存在一些问题。假设你想让自己的网页排名靠前一点，你只要创建很多僵尸网页，链接到你的网页就可以了。

还有一个问题:如果一个网页有很多指向其他网页的链接，那么这个网页的影响力就会过大。

21.2.2网页图的随机游走

改进方法：除了顶点的入度以外，还考虑了网页图上随机游走后到达每条边的概率。具体来说，他们将用户行为建模成以均匀分布的概率点击网页上的每一个链接。例如，你现在在x网页，给每条边x →y赋予一个以当前网页x为条件的条件概率:

于是，用户行为可以模拟为网络图上的随机游走。对所有指向y的边进行加和，可以计算到达特定网页y的概率:

考虑到没有向外链接的网页，在网页图中加入了超点，每个顶点都有一条指向超点的边。而且，超点以相等的概率指向其他每一个顶点，这样随机游走就可以在任意顶点重新开始。这一改造保证了网页图是强连通的。

如果一个网页中没有超链接，那么这个网页指向超点的边的概率等于1。如果网页中有超链接，那么指向超点的边的概率是某个特殊给定的概率。在最初的 Page Rank版本中，这个概率是0.15。即，每个出度n≥1的顶点，指向超点的边的概率等于0.15;而其他n个出边仍然是等概率的,即其他每条边的概率是0.85/n。

21.2.3平稳分布与网页排名

网页排名背后基本的思想是找到网页图的平稳分布，所以让我们来定义平稳分布。

假定随机游走始终不会离开图上的顶点，即要求

定义21.2.1：有向图的顶点概率分配是一个平稳分布，如果对所有顶点x

Sergey和 Larry将他们的网页排序定义为一个平稳分布。他们通过解线性方程组来确定这个平稳分布:对每个顶点x，找到非负数 Rank(x)，使得

这些数还必须满足附加约束:

他们设计出来的网页排序算法总能找到有意义的解。强连通图有唯一的平稳分布，引入超点保证了这一点。而且，从任意顶点开始，进行足够长的随机游走，最后位于每个网页的概率会越来越接近平稳分布。注意，没有超点的普通有向图可能不具备以下这两个性质:( 1)它们没有唯一的平稳分布;(2)即使存在平稳分布，从某些顶点出发经过随机游走后，不能收敛到平稳分布。