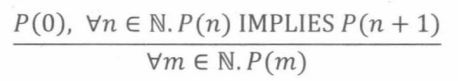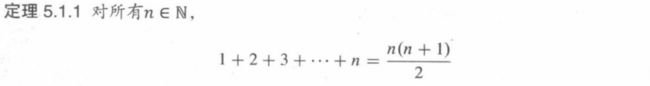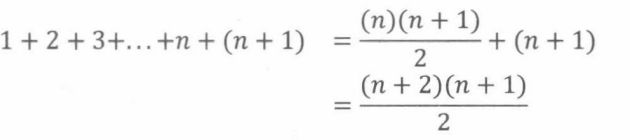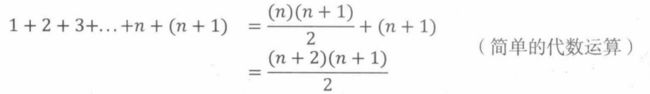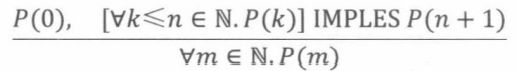第五章：归纳法
第五章：归纳法
归纳法：归纳法是证明某一特性对全体非负整数都为真的有力手段。归纳法的使用可以区分离散和连续这两种数学特征
只可以在非负整数上使用吗？
理论上，数学归纳法可以在任何良序集合上应用，但实数，复数没有自然的良序结构，需要先良序化再应用。
为什么区分离散和连续？
（个人想法，不知道对不对）具有连续数学特征的一组数据无法使用归纳法，因为无法通过P(n)去证明其下一项成立，因为在连续性随机变量中你根本不知道n的下一项是谁。其下一项是n+k，k是大于0，但无限接近于0的数。
5.1 一般归纳法
例子：
规定下面一些类命题：
5.1.1 一般归纳法的规则
原理：
由于以后还会学习归纳法的变种形式，所以我们将上述方法称为一般归纳法，归纳法法则如下：
5.1.2 举例说明
用归纳法证明以下定理的重要性：
归纳法证明定理的步骤如下：
- 定义谓词P
- 证明P(0)为真
- 对于任意的 n ∈ N n\in \Bbb N n∈N，P(n)可以推导出P(n+1)
- 采用数学归纳法得到，对于所有的非负整数m，P(m) 都成立
带入以上例子：
-
将以上的定理5.1.1定义为命题P。
-
当n = 0时，等式左边为0，等式右边为 0(0+1)/2 = 0。左边等于右边，所以P(0)为真。
-
通过P(n)成立推断P(n+1)成立，通过证明蕴含关系的基本方法，我们只需证明当P(n)为真时，P(n+1)时也为真即可。
当P(n)为真时：
我们只需在上式左右同时加上(n+1)，然后通过化简，即可得到下式
上式即为P(n+1)的情况。所以，通过P(n)成立可以推断出P(n+1)成立。
-
因此，根据归纳法规则，对所有非负整数m，P(m)都成立，从而定理得证。
5.1.3 归纳法的模板
归纳法大约可以分为5步：
- **陈述使用归纳法进行证明。**直截了当地陈述整体证明结构，有助于他人了解你的证明思路。
- 定义适当的谓词P(n)。
- **证明P(0)为真。**又称基本情形或基础步骤，通常来说比较简单。
- **证明P(n)蕴涵P(n＋1)对任意非负整数成立。**这步称之为归纳步骤。
- **得出结论。**至此，我们便可以得出结论:对于任意非负整数n，P(n)为真。
注：一定要明确标记基础步骤和归纳步骤，这样可以让证明过程更加清晰，同时能够避免遗忘关键的证明步骤。
5.1.4 一般归纳法的简洁写法
5.1.2中例子的证明由大量的无关的解释，我们可以提供一个更简洁的证明：
采用归纳法进行证明。归纳假设P(n)即为等式5.1。
**基础步骤:**当n =0时，因为等式5.1左右都为0，故P(O)为真。
**归纳步骤:**假设P(n)为真,即公式5.1在n为非负整数时成立。在等式左右两边同时加n +1可得
进而P(n +1)得证。所以，根据归纳法可知，对任意非负整数n,P(n)恒为真。
注：归纳法的这一特点有利有弊，弊端是归纳法无法帮助我们理解问题，而好处在于我们可以在不需要理解的情况下，保障数学证明的正确性。
5.1.5 更复杂的例子
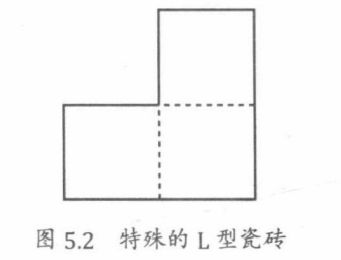
例子：一个边长为 2 n 2^n 2n的庭院，使用下面的特殊L型地砖进行铺设，肯定存在一种一种方法使其他地方都铺满，但中间留下一个空隙，建造Bill雕像。
注：这里说的在中间留空是相对的中间位置，如当n=2时，以下红框里面的任意一个位置都可以算是中间
错误证明示范：
令命题P(n)表示，对任意n≥0，大小为 2 n ∗ 2 n 2^n * 2^n 2n∗2n的庭院，存在某种中间是Bill雕像的铺设方案。
**基本步骤:**当n = 0时,整个庭院都是Bill，故P(O)为真。
**归纳步骤:**假设存在n≥0，使P(n)为真。我们需要证明当庭院大小 为 2 n + 1 ∗ 2 n + 1 为2^{n+1} * 2^{n+1} 为2n+1∗2n+1时，同样存在中间是Bill雕像的铺设方案。
对于以上的归纳假设很难去通过P(n)去证明P(n+1)，因此我们需要去换一个归纳假设。
正确的命题示范：
令命题P(n)表示在大小为 2 n ∗ 2 n 2^n * 2^n 2n∗2n的庭院中，对每一个Bill位置,剩下的部分存在铺设方案。
注：以上命题可能听上去有点奇怪，这里是对于归纳论证中一个很有意义的思想：如果我们不能证明一件事，那么我们就证明比它更大的事
**基础步骤:**当n =0时，整个庭院都是Bill，故P(O)为真。
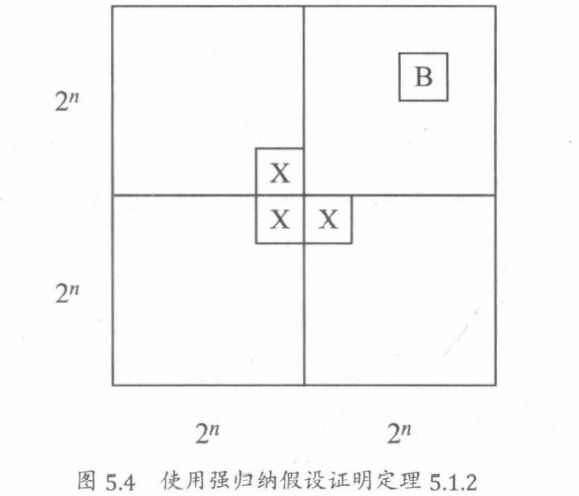
**归纳步骤:**假设存在n≥0，P(n)为真。即:在大小为 2 n ∗ 2 n 2^n * 2^n 2n∗2n的庭院中,对每一个Bill位置剩下的部分可以铺满。对于 2 n + 1 ∗ 2 n + 1 2^{n+1} * 2^{n+1} 2n+1∗2n+1的庭院，将其切分为4个 2 n ∗ 2 n 2^n *2^n 2n∗2n的子庭院。在其中一个子庭院中间放置Bill雕像（在图中用B表示),然后在其他三个子庭院中间各放一个雕像（在图中用X表示)，使这三个塑像组成L型。如图5.4所示。
得到了以上结论，我们只需将三个X替换为一个L型瓷砖即可证明P(n+1)成立。
根据归纳法，我们即可得知命题在大小为 2 n ∗ 2 n 2^n * 2^n 2n∗2n的庭院中，对每一个Bill位置,剩下的部分存在铺设方案成立。而待证明的定理其实即是P的一种特殊情形——雕像必须位于中心方格。
这个证明有两个特点
- 不仅证明了铺设方案的存在性，而且提供了如何进行铺设的算法。
- 得出了更强的结论:如果Bill想把雕像放在庭院的边缘位置，我们照样可以满足!
由以上可知，如果归纳证明行不通，使用更强的归纳假设是一个好办法。但需要注意的是，这个强假设必须为真，否则证明没有任何意义。有时候，确定合适的归纳假设并不是容易的事。
5.1.6 错误的归纳证明
证明如下错误定理：所有马的颜色都相同。即对于任意的n>=1匹马，他们的颜色相同。
归纳假设P(n)定义为：对于任意的n匹马，所有的马颜色相同。
**基础步骤:(n = 1)：**只有一匹马，这匹马的颜色当然与它自己相同，故P(1)为真。
**归纳步骤：**假设存在n≥1，P(n)为真。即假设有n匹马，它们的颜色相同。现在设我们有n ＋1匹马
那么 h 1 h_1 h1和 h n + 1 h_{n+1} hn+1的马都与 h 2 . . . . . . . h n h_2.......h_n h2.......hn颜色相同，可得这n+1匹马颜色都相同。
根据归纳法原则,对任意n≥1，P(n)都为真。
我们竟然用归纳法证明了一个错误的命题！
错误原因：以上的的证明方法并不受归纳法出了问题，而是我们在归纳步骤出了问题。当n = 1时， h 1 , h 2 , . . . . . . . . , h n , h n + 1 h_1,h_2,........,h_n,h_{n+1} h1,h2,........,hn,hn+1即变成了 h 1 , h 2 h_1,h_2 h1,h2，即不存在马既与 h 1 h_1 h1相同也与 h 2 h_2 h2相同，所以P(1)并不能推出P(2)。
错误的原因并不在于：P(n)本身为假，所以推出的P(n+1)也为假。因为在蕴含式中，前键为假，结果永远为真。
5.2 强归纳法
**强归纳法：**是归纳法的一个变种。强归纳法和归纳法的用途是–样的,都是用来证明某个谓词对全体非负整数成立。如果从n谓词为真无法直接得出n＋1谓词为真,但可以从其他≤n的情形推导而得,那就采用强归纳法。
5.2.1 强归纳法的规则
强归纳法与一般归纳法的唯一区别：
**一般归纳法：**一般纳法中,假设P(n)为真,证明P(n+1)也为真。
**强归纳法：**而在强归纳法中,你可以假设P(O),P(1)…P(n)全部为真，证明P(n +1)为真。
强归纳法法则如下：
强归纳法的证明模板与一般归纳法的几乎一样，除了以下两点：
- 陈述采用强归纳法证明
- 在归纳步骤中，假设P(0),P(1)…P(n)都为真，而不是只假设P(n)为真。
5.2.2 斐波那契数列
斐波那契数列的生成规则如下，以0和1开始，然后将前两个数相加得到下一个数，依次进行:
0 ， 1 ， 1 ， 2 ， 3 ， 5 ， 8 ， 13 ， 21......... 0，1，1，2，3，5，8，13，21......... 0，1，1，2，3，5，8，13，21.........
通过公式定义斐波那契额数列：
F ( 0 ) : : = 0 F(0) :: = 0 F(0)::=0
F ( 1 ) : : = 1 F(1) :: = 1 F(1)::=1
F ( n ) : : = F ( n − 1 ) + F ( n − 2 ) F(n) :: = F(n-1) + F(n-2) F(n)::=F(n−1)+F(n−2)
斐波那契数列的性质之一就是斐波那契数的奇偶性每隔三个数循环重复，即对于任意n，F(n)为偶数,当且仅当F(n＋3)为偶数。
下面我们采用归纳法去证明以上性质，因为F(n)与F(n-1)和F(n-2)都有关系，所有我们要采用强归纳法。
基本步骤：
(n = 0) F(0)=0和F(3)=2都是偶数。
(n = 1) F(1)=1和F(4)=3都不是偶数。
归纳步骤：
归纳步骤:对任意n≥1，假设P(n)和P(n -1)为真，我们需要证明P(n ＋1)为真。
对于任意整数k,m，易知：
注：m+k为偶数，即m和k要么同时为奇，要么同时为偶数。当m，k同时为奇数时，第二个IFF两边同时为假，公式成立。当m，k同时为偶数时，第二个IFF两边同时为真，公式成立。
证明过程为下：
5.2.4 找零问题
问题：采用3Sg面值的硬币和5Sg面值的硬币总能凑出任意不小于8Sg面值的硬币。
采用归纳法证明：
**归纳假设P(n)为：**存在一个硬币集合，其总面值为n+ 8Sg。
**基础步骤：**一个3Sg硬币和一个5Sg硬币即可凑成8Sg，故P(0)为真。
**归纳步骤：**假设对任意k≤n，P(k)为真，求证P(n＋1)为真。分类讨论如下。
当n = 0时，P(n+1)为面值为9Sg的情况，可以用3个面值为3Sg的组成。
当n = 1时，P(n+1)为面值为10Sg的情况，可以用2个面值为5Sg的组成。
当n >= 2时，当P(n+1)可以用一个面值为3Sg的硬币和P(n-2)的方案组合（该方案就是我们上面的假设P(k)）去组合。
以上三种情况即可涵盖所有情况了，有归纳法可知，我们以上的假设为真。
5.2.5 堆盒子游戏
游戏规则如下：
有n个堆放在一起的盒子。你可以移动这些盒子,每次移动只能将一堆盒子分成不为空的两堆盒子。最后得到n堆盒子，即每一堆只有一个盒子时，游戏结束。每次移动盒子时，玩家都会得分。得分规则是,如果将高度为a+ b的盒子堆,拆分成高度为a和b的两堆,玩家可以得ab分。玩家的总得分是每次移动盒子得分的加和。那么，怎样才能得到最高分呢?
**定理：**任何一种平铺n个盒子的方法，得分都为n(n -1)/2。
采用归纳法证明以上定理：
令归纳假设P(n)表示任何一种平铺n个盒子的方法，得分都为n(n - 1)/2。
**基础步骤：**当n = 1时，只有一个堆，所以不需要任何移动游戏即已经结束。总得分为1(1-1)/2=0。故P(1)为真。
**归纳步骤：**我们需要证明对任意n≥1,P(1),…P(n)蕴涵P(n +1)。为此，先假设P(1)…,P(n)都为真，然后分析n +1个盒子的堆。令第一次移动拆分成高度分别为a和b的两个堆，其中0
可见， P ( 1 ) , P ( 2 ) , . . . . . . P ( n ) P(1),P(2),......P(n) P(1),P(2),......P(n)推导出 P ( n + 1 ) P(n+1) P(n+1)
因此，由强归纳法可知，原命题为真。
5.3 强归纳法、一般归纳法和良序法比较
归纳法的证明模板看上去和良序原理完全不同，但其实本章的很多例子都已经在良序原理那一章证明过。事实上，任何基于良序原理的证明都可以自然而然地转化为归纳法证明。
反过来也很简单，即任何基于强归纳法的证明也可以自动转化为基于良序原理的证明。所以，良序、一般归纳法、强归纳法这三种证明方法，只不过是相同数学推导的三种不同形式。
那么，为什么需要三种方法?这是因为，有时候归纳法更清晰，因为归纳法不需要反证。而且,归纳法的递归过程,往往可以将大问题分解成小问题。另一方面，良序证明往往更简短，证明方式更接近我们平时思考的方式，对初学者更为友好。
反过来也很简单，即任何基于强归纳法的证明也可以自动转化为基于良序原理的证明。所以，良序、一般归纳法、强归纳法这三种证明方法，只不过是相同数学推导的三种不同形式。
那么，为什么需要三种方法?这是因为，有时候归纳法更清晰，因为归纳法不需要反证。而且,归纳法的递归过程,往往可以将大问题分解成小问题。另一方面，良序证明往往更简短，证明方式更接近我们平时思考的方式，对初学者更为友好。