白学立体视觉（3）: 单目相机标定

---

前言

小伙伴们，第一个理论加实践的小结来啦。本小节将会在白学立体视觉（2）: 相机内外参数与坐标系的基础上，介绍一下鼎鼎有名的张正友标定法。

---

一、为什么需要相机标定？

我们如果想重建出一台相机的成像过程的数学模型，相机的参数是最基本的。相机参数又分为内参和外参。那么内参和外参就是我们标定的最终目的。
1、有了内参中的畸变系数:[k1,k2,k3, …,p1,p2,…]，我们就可以对带畸变的图像进行矫正，避免采集到的图像产生桶形畸变和枕形畸变。
2、有了相机内外参数，我们就可以构建相机成像的几何模型，从而把世界坐标系中的三维物体投影到二维平面上。
3、计算多台相机中间的映射关系，本节不详细介绍，后边有的是机会。（这个很重要，这将是双目视觉乃至多目立体视觉基础）。

相机内参：相机的内参(dx,dy,r,u0,v0,f);
     一个像素在水平和垂直方向上的物理尺寸为dx和dy，单位为毫米(或者米)；
     焦距f，单位为毫米(或者米)；
     图像物理坐标的扭曲因子r，通常为0，忽略不计;
     u0,v0为主点在图像像素坐标系下的坐标，单位为像素；主点为过光心垂直于成像面的垂线，该垂线与成像面的交点。
相机外参：[R|T]；
     世界坐标系转换到相机坐标系的旋转R和平移T矩阵。
畸变系数：[k1,k2,k3, …,p1,p2,…]。
     我们只关心相机的径向畸变系数k1,k2,k3…，和相机的切向畸变系数p1,p2,~。

二、张正友标定法

1.标定板

张正友标定法应用比较广泛，操作也比较简单易实现。只需要一个角点特征明显，且易于提取的平面板。如下图所示：
标定板有以下几个制作要求：
1、标定板是一个二维平面。
2、标定板不反光，不透视，不易变形。
3、角点之间的物理距离是固定的，根据需要可以设为7cm，11cm等。

2.公式命名

  本节公式主要来源于张正友论文，感兴趣的可以阅读一下原论文。
  2D图像点坐标及其齐次坐标：
  3D空间点坐标及其齐次坐标：
  3D空间点到图像像素坐标的映射关系用下式表示：

s:表示3D空间坐标系到图像坐标系的尺度因子
A:相机内参矩阵
(u0,v0):像主点坐标，
α , β：分别为图像u轴和v轴方向的焦距值（像素单位），也就是上小结中提到的ax、ay(ax 和 ay 被称为等效焦距,有时候也用Fx 和 Fy表示)
γ：为像元轴的倾斜因子

3.理论介绍

标定板是一个平面，所以角点都位于一个空间平面上，我们可以让标定板上左上角的第一个角点设为世界坐标系的原点(0, 0, 0)，让Z轴垂直于标定板平面，所以标定板上的所有角点的Z坐标都为0，即角点的空间三维坐标可以用下式表示：

同时，旋转矩阵R的第i列可以用 ri 表示，[r1,r2,r3]和t分别是相机坐标系相对于世界坐标系的旋转矩阵和平移向量。其中角点Z坐标全部为0，所以：

这里涉及一个很重要的概念：单应性矩阵H，是一个3 × 3的矩阵，简单提及一下这个矩阵，只要记住它包含了相机内参和外参即可，后续小结会详细介绍。于是，空间到图像的映射关系就可以用下式表示：

其中单应性矩阵H可以用下式表示，λ 是一个任意标量（λ 表示齐次坐标的尺度不变性，也可以认为λ = 1）：

单应性矩阵是一个3 × 3的矩阵，也可以用下式表示：

根据旋转矩阵的性质，即R为单位正交阵，所以r1和r2是标准正交基，相互垂直且模长均为1（旋转向量的模为1，旋转不改变尺度）。

结合上式可以得到：

根据旋转矩阵R的列向量正交和向量模为1这两个约束条件，经过一下数据变化可以得到：

通过上面的式子，很容易看出，单应性矩阵H和内参矩阵A的元素之间满足两个线性方程约束。h1和h2是通过单应性矩阵求解出来的，所以我们要求解的参数就变成A矩阵中未知的5个参数。我们可以通过三个单应性矩阵来求解这5个参数，利用三个单应性矩阵在两个约束下可以生成6个方程。其中，三个单应性矩阵又可以通过三张标定板图像获得，但是这三张图像是对同一标定板在不同角度和高度采集得到。

4.相机参数求解过程

我们令

B是一个对称阵，所以B的有效元素就剩下6个，即：

设H的第i列为hi:

根据b的定义，进一步化简得到：

通过计算，可以得到：

利用上面提到的两个约束条件，我们可以得到下面的方程组：

这是一个标准的线性方程组V b = 0 ，大学时线性代数老师教我们的线性方程组的求解方法还记得吗？哈哈哈。
如果有n组观察图像，则V 是 2n x 6 的矩阵，根据最小二乘定义，V b = 0 的解是VTV 最小特征值对应的特征向量。

因此, 可以直接估算出 b，后续可以通过b求解内参。因为B中的未知量为6个，所以当观测平面 n ≥ 3 时，可以得到b的唯一解
当 n = 2时, 一般可令畸变参数γ = 0
当 n = 1时, 仅能估算出α 与 β, 此时一般可假定像主点坐标 u0 与 v0 为0
内部参数可通过如下公式计算(cholesky分解)：

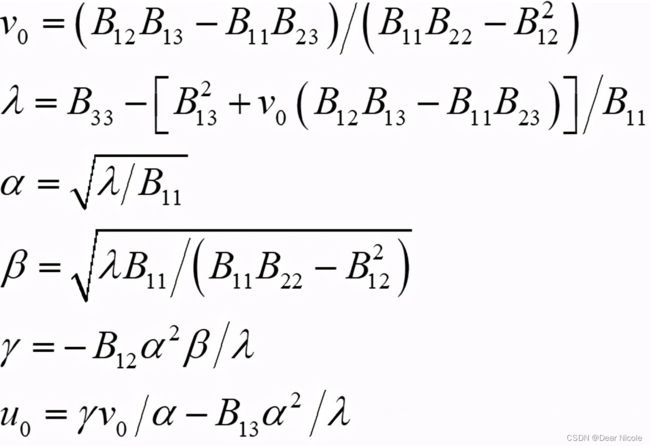
有了内部参数矩阵A，再根据

化简计算得到以下外部参数：

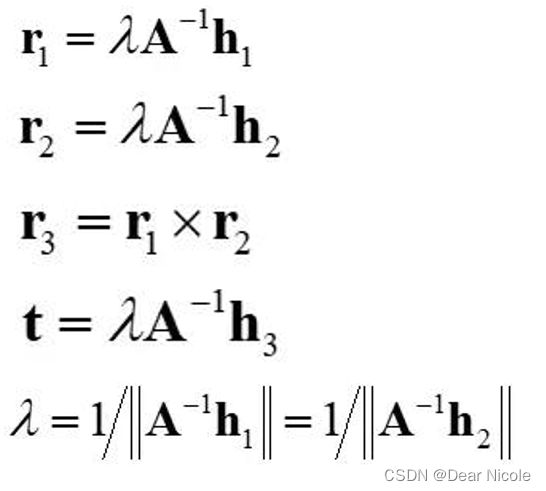
由于图像噪声等因素的影响，上述过程求得的 CCD 相机参数与真实值之间还存在着差距。使用最大似然估计进行优化。
因此，需要对所有的相机参数进行最优化求解，优化目标函数为：

其中n为标定板图像数量，m为标定板上角点数量。
mij 是通过角点检测得到的像素坐标点。
m~为世界坐标系一点M通过相机成像模型投影得到的二维点坐标。
这是一个非线性表达式，所以这是一个非线性最小化求解问题，可以用Levenberg-Marquardt算法来求解。

5.相机畸变

以上的公式推导都没有考虑相机的畸变问题，现实情况下，很难有相机厂商能做出没有畸变的相机。上个小结已经对相机畸变进行了详细介绍。我们主要考虑两种畸变：径向畸变和切向畸变。一般的相机只要计算径向畸变的前三项：k1,k2,k3和切向畸变的前两项：p1,p2就可以得到很好的畸变矫正效果。而在一些畸变比较大的相机中，比如鱼眼相机，要想比较好的去处畸变，就需要计算更多项参数。
张正友标定法只考虑了最大的径向畸变：k1,k2。数学表达式为：

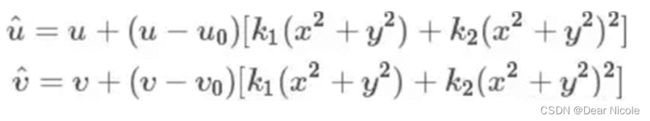
其中，(u,v)是理想的无畸变的像素坐标，(^u， ^v)是实际畸变后的像素坐标，在这里就是角点检测得到的角点坐标，(u0,v0)代表主点。
(x,y)是理想无畸变的连续图像坐标，(^x, ^y)是实际畸变后的连续图像坐标。k1和k2为前两阶的畸变参数。

从而得到畸变公式的矩阵形式：

记做：Dk=d

将上面计算的内参数代入公式：

得到近似理想条件下的角点坐标( u , v ) 。然后根据畸变公式计算近似的畸变系数k1和k2。

最后就可以建立新的最大似然估计表达式：

通过非线性求解方法来求解所有内外参数和畸变系数。

到这里，张正友标定法就计算出来我们想要的相机内参、相机外参和畸变系数。

三、OpenCV实践张氏标定法

1.标定步骤

1、准备一个标定板，按照上文提出的要求制作。为了简便也可以用A4纸打印，粘贴在一个平板上。
2、采集棋盘格标定板若干张图片，一般10至20张就够。但是每次拍摄，标定板角度和位置要改变。
3、检测图片中角点。
4、利用解析解估算方法计算出5个内部参数，以及6个外部参数
5、使用畸变公式的线性方程组求解近似的畸变系数（或者直接使用0也可以）
6、使用非线性优化法计算精确的内外参数和畸变系数。

2.标定实践

代码如下（示例）：

# -*- coding:utf-8 -*-
import os
import cv2
import numpy as np
import glob
import configparser

class MonocularCalibration(object):
    '''单目标定和矫正类'''
    def __init__(self, data_root, cali_file="MonoCalib_Param_720p.ini", board_size=(7,11), img_shape=(720, 1280), suffix="png"):
        self.cali_file = os.path.join(data_root, cali_file)
        self.H, self.W = img_shape
        if os.path.exists(self.cali_file):
            print("\n===> Read Calibration file from {}...".format(self.cali_file))
            self.read_cali_file(self.cali_file)
        else:
            print("\n===> Start Calibration...")
            # 步骤1：初始化
            self.board_size = board_size
            # 步骤2：标定
            self.Mono_Calibration(corner_h=self.board_size[0], corner_w=self.board_size[1], source_path=data_root, suffix=suffix)
            # 步骤3：生成标定文件
            self.write_cali_file(cali_file=self.cali_file)

    # 计算单目相机内参、畸变系数
    def Mono_Calibration(self, corner_h, corner_w, source_path, suffix="png"):
        # 设置寻找亚像素角点的参数，采用的停止准则是最大循环次数30和最大误差容限0.001
        criteria = (cv2.TERM_CRITERIA_MAX_ITER | cv2.TERM_CRITERIA_EPS, 30, 0.001)
        # 获取标定板角点的位置
        # 世界坐标系中的棋盘格点,例如(0,0,0), (1,0,0), (2,0,0) ....,(8,5,0)，去掉Z坐标，记为二维矩阵
        objp = np.zeros((corner_h * corner_w, 3), np.float32)
        # 将世界坐标系建在标定板上，所有点的Z坐标全部为0，所以只需要赋值x和y
        objp[:, :2] = np.mgrid[0:corner_w, 0:corner_h].T.reshape(-1, 2)
        square_size = 50.0  # 18.1  # 18.1 mm
        objp = objp * square_size

        # 储存棋盘格角点的世界坐标和图像坐标对
        obj_points = []  # 存储3D点  # 在世界坐标系中的三维点
        img_points = []  # 存储2D点  # 在图像平面的二维点

        images = glob.glob(os.path.join(source_path, "*." + suffix))
        for index, fname in enumerate(images):
            print("=== ", index)
            img = cv2.imread(fname)
            h_, w_, _ = img.shape
            if h_ != self.H or w_ != self.W:
                img = cv2.resize(img, (self.W, self.H), interpolation=cv2.INTER_CUBIC)

            self.gray = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)
            size = self.gray.shape[::-1]
            ret, corners = cv2.findChessboardCorners(self.gray, (corner_w, corner_h), None)

            if (corners[0, 0, 0] < corners[-1, 0, 0]):
                print("*" * 5 + " order of {} is inverse! ".format(index) + "*" * 5)
                corners = np.flip(corners, axis=0).copy()

            if ret:
                obj_points.append(objp)
                corners2 = cv2.cornerSubPix(self.gray, corners, (11, 11), (-1, -1), criteria)  # 在原角点的基础上寻找亚像素角点
                img_points.append(corners2)

                cv2.drawChessboardCorners(img, (corner_w, corner_h), corners2, ret)  # 记住，OpenCV的绘制函数一般无返回值
                cv2.imshow('img', img)
                cv2.waitKey(50)

        cv2.destroyAllWindows()

        # print("img_points: ", img_points.shape)
        # print("obj_points: ", obj_points.shape)

        # 标定
        ret, self.mtx, self.dist, self.rvecs, self.tvecs = cv2.calibrateCamera(obj_points, img_points, self.gray.shape[::-1], None, None)

        print("ret:", ret)
        print("mtx:\n", self.mtx)  # 内参数矩阵
        print("dist:\n", self.dist)  # 畸变系数   distortion cofficients = (k_1,k_2,p_1,p_2,k_3)

        # 并且通过实验表明，distortion cofficients = (k_1,k_2,p_1,p_2,k_3)
        # 三个参数的时候由于k3所对应的非线性较为剧烈。估计的不好，容易产生极大的扭曲，所以k_3强制设置为0.0
        # self.dist[0, 4] = 0.0

        return self.mtx, self.dist, self.rvecs, self.tvecs

    def Mono_Undisort_list(self, source_path, suffix="png"):
        # 对所有图片进行去畸变，有两种方法实现分别为： undistort()和remap()
        images = glob.glob(os.path.join(source_path, "*." + suffix))
        for fname in images:
            fname = '/'.join(fname.split('\\'))
            print(fname)
            prefix = fname.split('/')[-1].replace(".", "_undistort.")
            # print(prefix)
            img = cv2.imread(fname)
            h_, w_, _ = img.shape
            if h_ != self.H or w_ != self.W:
                img = cv2.resize(img, (self.W, self.H), interpolation=cv2.INTER_CUBIC)


            dst = self.Mono_Rectify(img, flag=True)


            print("img: ", img.shape)
            print("dst: ", dst.shape)
            # cv2.imshow('img', img)
            # cv2.imshow('dst', dst)
            #
            # cv2.waitKey(500)

            if not os.path.isdir(os.path.join(source_path, "mono_rec")):
                os.mkdir(os.path.join(source_path, "mono_rec"))
            cv2.imwrite(os.path.join(source_path, "mono_rec", prefix), dst)

    def Mono_Rectify(self, image, flag=True):
        image = cv2.resize(image, (self.W, self.H))

        # 使用 cv.undistort()进行畸变校正
        if flag:
            # 矫正单目图像：直接使用计算的相机内参矩阵
            image_rec = cv2.undistort(image, self.mtx, self.dist, None, self.mtx)

        else:
            # 矫正单目图像：使用计算的相机内参矩阵计算新的内参矩阵
            '''
            1、默认情况下，我们通常不会求取新的CameraMatrix，这样代码中会默认使用标定得到的CameraMatrix。
                而这个摄像机矩阵是在理想情况下没有考虑畸变得到的，所以并不准确，重要的是fx和fy的值会比考虑畸变情况下的偏大，
                会损失很多有效像素。我们可以通过这个函数getOptimalNewCameraMatrix ()求取一个新的摄像机内参矩阵，
            2、cv2.getOptimalNewCameraMatrix()。如果参数alpha = 0, 它返回含有最小不需要像素的非扭曲图像，
                所以它可能移除一些图像角点。如果alpha = 1， 所有像素都返回。还会返回一个 ROI 图像，我们可以用来对结果进行裁剪。
            '''
            h, w = self.H, self.W
            newcameramtx, roi = cv2.getOptimalNewCameraMatrix(self.mtx, self.dist, (w, h), 0, (w, h))
            image_rec = cv2.undistort(image, self.mtx, self.dist, None, newcameramtx)
            # crop and save the image
            # x, y, w, h = roi
            # image_rec = image_rec[y:y + h, x:x + w]

        return image_rec

    def read_cali_file(self, cali_file):
        con = configparser.ConfigParser()
        con.read(cali_file, encoding='utf-8')
        sections = con.sections()
        # print(sections.items)
        calib = con.items('Calib')
        rectify = con.items('Rectify')
        calib = dict(calib)
        rectify = dict(rectify)

        self.u0 = calib['u0']
        self.v0 = calib['v0']
        self.fx = calib['fx']
        self.fy = calib['fy']

        self.mtx = np.array([[rectify['mtx_0'], rectify['mtx_1'], rectify['mtx_2']],
                            [rectify['mtx_3'], rectify['mtx_4'], rectify['mtx_5']],
                            [rectify['mtx_6'], rectify['mtx_7'], rectify['mtx_8']]]).astype('float32')

        self.dist = np.array([[rectify['dist_k1'],
                               rectify['dist_k2'],
                               rectify['dist_p1'],
                               rectify['dist_p2'],
                               rectify['dist_k3']]]).astype('float32')

    def write_cali_file(self, cali_file="./MonoCalib_Param.ini"):
        self.u0 = self.mtx[0, 2]
        self.v0 = self.mtx[1, 2]
        self.fx = self.mtx[0, 0]
        self.fy = self.mtx[1, 1]
        self.Calib = {"fx": self.fx,
                      "fy": self.fy,
                      "u0": self.u0,
                      "v0": self.v0,
                     }
        # 相机内参矩阵
        # fx  s   x0
        # 0   fy  y0
        # 0   0    1
        Rectify = {}
        for i in range(3):
            for j in range(3):
                Rectify['mtx_{}'.format(i*3+j)] = self.mtx[i, j]

        # 相机畸变系数
        # 畸变系数   distortion cofficients = (k_1,k_2,p_1,p_2,k_3)
        Rectify['dist_k1'] = self.dist[0, 0]
        Rectify['dist_k2'] = self.dist[0, 1]
        Rectify['dist_p1'] = self.dist[0, 2]
        Rectify['dist_p2'] = self.dist[0, 3]
        Rectify['dist_k3'] = self.dist[0, 4]

        self.Rectify = Rectify
        # Write calibration param to file.
        config = configparser.ConfigParser()
        config["Calib"] = self.Calib
        config["Rectify"] = self.Rectify
        # with open("Calib_Param_4.ini", 'w') as configfile:
        with open(cali_file, 'w') as configfile:
            config.write(configfile)


def main():
    source_path = "path to your image"
    mono_calibration = MonocularCalibration(data_root=source_path,
                                            cali_file="MonoCalib_Param_720p.ini",
                                            board_size=(7, 11),
                                            img_shape=(720, 1280),
                                            suffix="png")
    print(mono_calibration.mtx)
    print(mono_calibration.dist)
    data_root = source_path
    mono_calibration.Mono_Undisort_list(data_root, suffix="png")


if __name__ == '__main__':
    main()

矫正效果：

这个代码我测试过，效果还可以。里面加了一些注释，相信大家可以理解。小伙伴们也可以调一下参数，以便得到自己想要的效果。

---

总结

本小节主要是对张正友标定法进行了相机的介绍，希望各位有所收获。当然了这只是比较基础的单目标定过程，是双目视觉的基础。后边小节我们将进一步学习双目视觉立体标定的相关知识。