numpy.interp()用法
numpy.interp()主要使用场景为一维线性插值,我在直接看官方文档时一下子没有明白,后来结合图像绘制才明白它的用法,下面我们使用官方代码示例和我给出的图像对其进行简单介绍。
首先官方对该函数的解释是:
一维线性插值.
返回离散数据的一维分段线性插值结果.
参数
x: 数组
待插入数据的横坐标.
xp: 一维浮点数序列
原始数据点的横坐标,如果period参数没有指定那么就必须是递增的。否则,在使用xp = xp % period正则化之后,xp在内部进行排序.
fp: 一维浮点数或复数序列
原始数据点的纵坐标,和xp序列等长.
left: 可选参数,类型为浮点数或复数(对应于fp值),当x < xp[0]时的插值返回值,默认为fp[0].
right: 可选参数,类型为浮点数或复数(对应于fp值),当x > xp[-1]时的插值返回值,默认为fp[-1].
period: None或者浮点数,可选参数. 横坐标的周期. 此参数使得可以正确插入angular x-coordinates. 如果该参数被设定,那么忽略left参数和right参数。
返回值
浮点数或复数(对应于fp值)或ndarray. 插入数据的纵坐标,和x形状相同。
下面我们一起看一下官方给的几个示例,在这之前需要注意的是,在没有设置period参数时,默认要求xp参数是递增序列,可以使用下述代码进行检查:
np.all(np.diff(xp) > 0)
第一个示例:
import numpy as np
import matplotlib.pyplot as plt
x = 2.5
xp = [1, 2, 3]
fp = [3, 2, 0]
y = np.interp(x, xp, fp) # 1.0
plt.plot(xp, fp, '-o')
plt.plot(x, y, 'x')
plt.show()
输出图像为:

可以看到当x等于2.5时,在蓝色折线(原始数据构成的图线)上可以找到y=1.0为插入坐标的纵坐标。
第二个示例:
x = [0, 1, 1.5, 2.72, 3.14]
xp = [1, 2, 3]
fp = [3, 2, 0]
y = np.interp(x, xp, fp) # array([ 3. , 3. , 2.5 , 0.56, 0. ])
plt.plot(xp, fp, '-o')
plt.plot(x, y, 'x')
plt.show()
输出图像为:

当对应的x序列为[0, 1, 1.5, 2.72, 3.14]时,得到的y序列是[ 3. , 3. , 2.5 , 0.56, 0. ],需要注意的是当x=0时,由于0 < xp[0],所以y被设定为fp[0],也就是3,当x=3.14时,由于3.14 > xp[-1],则y被设定为fp[-1],也就是0。
第三个示例:
x = 3.14
xp = [1, 2, 3]
fp = [3, 2, 0]
UNDEF = -99.0
y = np.interp(x, xp, fp, right=UNDEF) # -99.0
plt.plot(xp, fp, '-o')
plt.plot(x, y, 'x')
plt.show()
输出图像为:

这里将right设置为-99.0,使得x=3.14 > xp[-1]时,y取值为-99.0,同理可以对x < xp[0]的值进行设置。
第四个示例:
x = np.linspace(0, 2 * np.pi, 10)
y = np.sin(x)
xvals = np.linspace(0, 2 * np.pi, 50)
yinterp = np.interp(xvals, x, y)
plt.plot(x, y, 'o')
plt.plot(xvals, yinterp, '-x')
plt.show()
输出图像为:
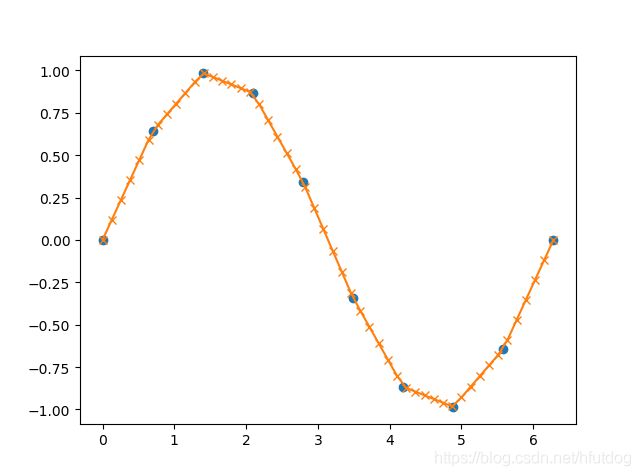
上图展示的是在正弦函数图像上进行插值,可以看到黄色叉叉连成的是一段段折线,这也就是利用线性插值对正弦函数进行逼近的效果。
以上示例对numpy.interp()的基本使用已经够了,还有一个参数period如何去使用以及官方给的示例我还没有搞清楚,以后弄懂了会补上,当然,如果各位读者朋友有知道的也欢迎在评论区加以指教。
参考文章:
numpy的一维线性插值函数