梯度下降法实战案例（波士顿房价）

本次实战思路是先找到波士顿房价数据中与房价有较强相关性的一列数据，通过梯度下降法找合适的参数，拟合出这列数据与房价的线性关系。

直接上代码

from sklearn.datasets import load_boston
import matplotlib.pyplot as plt
import pandas as pd
import seaborn as sns
import numpy as np
import random
%matplotlib inline

dataset = load_boston()#导入数据集
dataframe = pd.DataFrame(dataset['data'])#将数据转成DataFrame格式
dataframe.columns = dataset['feature_names']#添加列索引
dataframe#打印数据

dataframe['price'] = dataset['target']#增加“price”列
dataframe.head()

sns.heatmap(dataframe.corr(), annot=True, fmt='.1f')
#根据相关系数画出热力图，其中越接近1说明这两列数据正相关性越强

基于以上分析，卧室数量和房价正相关较强，我们可以根据卧室数量估计房子价格。

X_rm = dataframe['RM'].values
Y = dataframe['price'].values
rm_to_price = {r: y for r, y in zip(X_rm, Y)}
rm_to_price

可以把卧室数量作为字典的键，房价作为值。用键查找值，假如字典中没有要查询的卧室数量，就会报错。

第一种方法：用K-NN算法思想估计出卧室数量与房价的对应关系

#topn：邻居数量
def knn(history_price, query_x, topn=3):
    #找出与query_x距离最近的topn个卧室数量
    most_similar_items = sorted(history_price.items(), key=lambda e:(e[0] - query_x)**2)[:topn]
    #找出对应的房子价格
    most_similar_prices = [price for rm, price in most_similar_items]
    #求出价格的平均值作为输出结果
    average_prices = np.mean(most_similar_prices)
    
    return average_prices

进行测试

#7个个卧室的房价大约是29.23334
knn(rm_to_price, 7)

#画出卧室数量与房价的散点图 
plt.scatter(X_rm, Y)

散点图给我们提供了另外一种思路，将X_rm和Y拟合成一条直线，找到合适的k和b，我们只需把卧室数量作为变量输入，即可输出得到房价。
第二种方法：拟合线性函数

• 损失函数
  $$Loss(k,b)=\frac{1}{n}\sum _{i\in N}(\widehat{y_i}-y_i{)}^2$$
  $$Loss(k,b)=\frac{1}{n}\sum _{i\in N}((k\ast r{m}_i+b)-y_i{)}^2$$

• 对k求偏导
  $$\frac{\partial loss(k,b)}{\partial k}=\frac{2}{n}\sum _{i\in N}(k\ast r{m}_i+b-y_i)\ast r{m}_i$$

• 对b求偏导
  $$\frac{\partial loss(k,b)}{\partial b}=\frac{2}{n}\sum _{i\in N}(k\ast r{m}_i+b-y_i)$$

#损失函数，在这里用的是MSE
def loss(y, yhat):
    return np.mean(np.array(y) - np.array(yhat) ** 2)

#代入k和b，返回预测结果
def model(x, k , b):
    return x * k + b

#对k求偏导
def partial_k(x, y, k, b):
    return 2 * np.mean((y - (k * x + b)) * (-x))#为什么是负值

#对b求偏导
def partial_b(x, y, k, b):
    return 2 * np.mean((y - (k * x + b)) * (-1))

梯度下降过程：
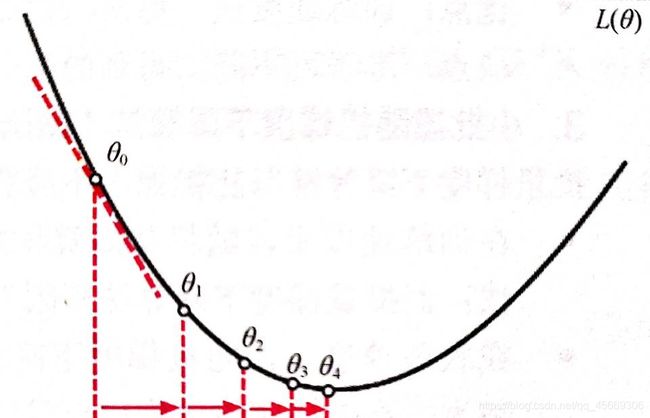
在微积分中，对多元函数的参数求偏导数，求得参数的偏导数以向量形式表达就是梯度。如图所示，θ₀到θ₁的距离为θ₀在函数L(θ)上的梯度，记做∂L / ∂θ。

在数学上，梯度越大，则函数的变化越大。对于函数L(θ)在点θ₀处，梯度向量∂L / ∂θ的方向就是函数L(θ)增加最快的方向。也就是说，沿着梯度向量的方向易于找到函数的最大值。反之亦然，沿着梯度向量相反的方向，梯度减少最快，易于找到函数的最小值。

假设函数L(θ)为损失函数，为了找到损失函数的最小值，需要沿着与梯度向量相反的方向 -∂L / ∂θ更新变量θ，这样可以使梯度减少最快，直到损失收敛至最小值。其基本公式：
$$\theta \leftarrow \theta -\eta \frac{\partial L}{\partial \theta }$$

其中，η∈R为学习率，用于控制梯度下降的幅度（快慢）。看上图，梯度下降算法每次计算参数θₓ在当前位置的梯度，然后让参数θₓ顺着梯度的反方向前进一段距离，不断重复该过程。直到梯度接近于零的时候，算法认为找到了损失函数L(θ)的最小值并停止计算。 此时可以认为参数θ*恰好到达让损失函数位于最小值的状态。

VAR_MAX, VAR_MIN = 100, -100#k、b随机取值范围
k, b = random.random(), random.random()
    
min_loss = float('inf')
best_k, best_b = None, None

total_times = 5000#迭代次数
alpha = 1e-2#学习率

k_b_history = []

for t in range(total_times):
    #梯度下降法找k、b的值
    k = k + (-1) * partial_k(X_rm, Y, k, b) * alpha
    b = b + (-1) * partial_b(X_rm, Y, k, b) * alpha
    loss_ = loss(Y, model(X_rm, k, b))
    if loss_ < min_loss:
        min_loss = loss_
        best_k, best_b = k, b
        k_b_history.append((best_k, best_b))
        #print('在{}时刻 我找到了更好的k:{}和b：{}， 这个时候的loss是{}'.format(t, k, b, loss_))

把结果print一下，可以看到几乎在每一个时刻的损失函数值都比上一时刻的更优，说明使用梯度下降法是有效的。

#打印最终的损失函数值
min_loss

#查看拟合效果
plt.scatter(X_rm, Y)
plt.plot(X_rm, best_k * X_rm + best_b, 'yo')

比较两种方法用时

%%time
model(6, best_k, best_b)

%%time
knn(rm_to_price, 6)

事实证明第二种方法比第一种快将近一百万倍！！！

有人会提出来说训练模型的耗时不算嘛？但是相对于knn每次用时那么久，训练出模型一劳永逸就太香了。

本次实战到这里就结束了，假如有喜欢可视化的同学可以透视一下训练过程。

#透视拟合过程
#选取某几个范围内的时刻
test_0 = 0
test_1 = 10
test_2 = 100
test_3 = 5000
test_4 = -1

plt.scatter(X_rm, Y)
plt.scatter(X_rm, k_b_history[test_0][0] * X_rm + k_b_history[test_0][1], color='red')
plt.scatter(X_rm, k_b_history[test_1][0] * X_rm + k_b_history[test_1][1])
plt.scatter(X_rm, k_b_history[test_2][0] * X_rm + k_b_history[test_2][1])
plt.scatter(X_rm, k_b_history[test_3][0] * X_rm + k_b_history[test_3][1])
plt.scatter(X_rm, k_b_history[test_4][0] * X_rm + k_b_history[test_4][1])

完！