计算机图形学-正交投影与透视投影

本专栏内容整理了GAMES101的计算机图形学课程的主要内容，作为我学习计算机图形学的一份复习备份或叫做笔记。内容中如有错误，或有其他建议，欢迎大家指出。

附上GAMES101计算机图形学课程：GAMES101: 现代计算机图形学入门正在上传…重新上传取消https://sites.cs.ucsb.edu/~lingqi/teaching/games101.htmlhttps://sites.cs.ucsb.edu/~lingqi/teaching/games101.html

GAMES101-现代计算机图形学入门-闫令琪_哔哩哔哩_bilibiliGAMES101-现代计算机图形学入门-闫令琪共计23条视频，包括：Lecture 01 Overview of Computer Graphics、Lecture 02 Review of Linear Algebra、Lecture 03 Transformation等，UP主更多精彩视频，请关注UP账号。正在上传…重新上传取消https://www.bilibili.com/video/BV1X7411F744https://www.bilibili.com/video/BV1X7411F744

开始讲解前让我们先回忆下我们平时拍照的一个过程：
首先找一个地方，把所有人都集中在这个地方中。这个过程就是模型变换（改变人的位置）
然后找一个好的位置，和一个好的角度，把相机放好。这个过程就是视图变换（改变相机）
最后按下快门把相机中看到的场景投影到相片上。这就是投影变换。

在图形学中，要得到一个画面跟我们平时拍照的过程是类似的。主要就是通过三个变换过程来得到要显示的画面。

视物变换

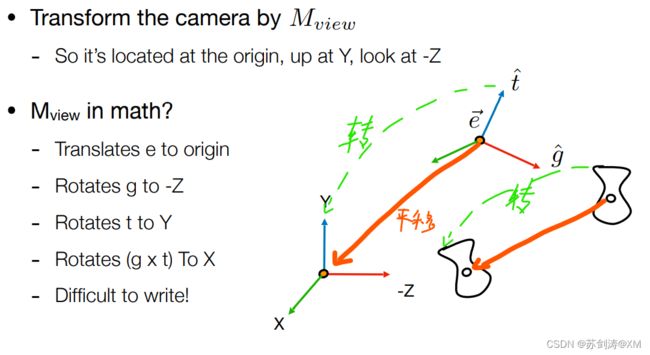
怎么做视图变换，即我们刚刚说的该如何摆放相机，
即确定：相机放置的位置（position），
和相机应该看向哪里（lookAt）。
此外，还需要定一个相机的向上方向（up），可以理解为相机是竖着拿还是横着拿。

通常，我们把相机永远放在原点上（0,0,0,）。相机沿着-z方向上看。向上方向是y。
position:(0,0,0,1);
lookAt:(0,0,-1,0);
up:(0,1,0,0)

写成矩阵形式：先平移后旋转 ==》

平移：

旋转：当我们要写一个由任意方向向量旋转到x轴上的矩阵会比较困难。但是我们可以利用旋转矩阵是个正交矩阵的特性。先写出由x轴旋转到原方向向量的矩阵，即是方向向量转到x轴的旋转矩阵的逆矩阵。再为原向量应用这个再去求矩阵转置即可把向量旋转到x轴上。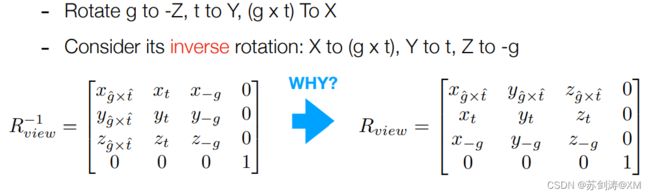

应用矩阵：

到x(1,0,0,0)T 可得到 ，把y，和-z带入可以得到t和g向量。所以这个矩阵就是相机的旋转矩阵的逆矩阵。对其转置就能得到相机的旋转矩阵:

再将相机放置好后，其他的物体与相机的相对位置发生了变化，所以我们还需要对场景中的物体做跟相机一样的变换使其相对位置和相对角度都不变。（比如我现在渲染的是一副从上向下看的图，再移动相机后，相机接收到的画面就会变成正视图，所以还需要将被观察的物体做相同的平移和旋转。之后相机接收到的画面就还是和之前的俯视图一样。注意旋转都是围绕原点旋转。）
 

投影

视图和模型变换结束后，接下来就是吧三维的场景变成观测到的二维的图像。这就是投影。
投影分为正交投影和透视投影。其中透视投影跟我们平时人眼观测到的成像差不多。正交投影就比较难以理解，其实就是不发生近大远小的变化，成像后会人类会觉得远处的东西更大。几何上来说就是，正交投影中平行的线成像后依旧平行。

                       

正交投影（Orthographic Projection）

 在三维空间中规定可观测区域，这个区域是个立方体。需要设置它的宽度(right-left)，
高度(top-bottom)和深度(near-far(看向-z所以n比f大))六个数据。在将这个立方体移动、缩小或放大到挤满X(-1~1),Y(-1~1),Z(-1~1)的立方体区域内（这里是约定俗成的做法，是为了后续一些计算）。

 所以正交投影的变换矩阵

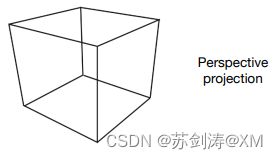
透视投影（Perspective Projection）

在透视投影中会发生近大远小的情况，由近到远的平行线，看起来会在非常非常远的地方相交，该怎么处理出这种成像效果呢？这就是透视投影变换需要做的事。

首先我们观察下图中的几何体：

这是类似自然人的视野范围，或者叫做视锥体，它有一个比较小的近平面和一个比较大的远平面，这两个平面是近似等比关系。他们的中心点的x，y坐标都是0(观察点在原点)。

我们发现，当我们将远缩小成跟近平面一样的大小后，锥体会变成一个长方体，接下去我们只要做正交投影即可完成一个透视投影了。

锥体变换成长方体（FrustumToCuboid）Mpersp->ortho
首先我们观察在变换的过程中有以下几个特点：
1.变换后近平面的任何点都不变
2.变换后远平面的z不变（但是并不是说在近平面和远平面之间的平面z的值不会变）
3.变换后远平面的中心点不会变

然后由上图我们可以根据相似三角形知道，在任意z点的平面上，缩小后的平面的x和y会变成n/z倍，只剩变化后的z值我们还未可知。
由此我们可以写出矩阵运算过程如下图：

要求的变换矩阵只剩第三行的元素我们还不清楚了。接下来根据之前列出来的三点变换特点，我们可以对第三行的元素进行推算。
首先根据第一点，我们将近平面的点(x,y,n,1)T 带入变换矩阵运算可以知道第三行的运算如下：

 ?x +?y +?n +? = n² ；所以可以确定n²跟x和y没有关系，也就确定了第三行前两个元素是0；我们把后两个元素标记为A，B。

于是我们可以根据第一点列出：An + B = n²  (在近平面上的点不会变)
       根据第二点和第三点列出：An + B = f² （在远平面上的z不会变，远平面中心点(0,0,f,1)不变）
        这里采用特殊点带入的方式即可列出方程；
解方程：

于是我们得到最终的锥体变换成长方体的变换矩阵：Mpersp->ortho

最后透视投影的变换矩阵：Mpersp =  Mpersp->ortho

最后的最后，思考一个问题：在近平面和远平面之间的平面经过Mpersp->ortho变换后z的值会如何变化？变大？变小？不变？

思路：找到图中铁路的中心点，可以看到在图片的上方木枕越来越多，铁路的中心点则肯定在上部分，也就是越来越远的地方，所以可以看出，中间的z会变小（看向的是-z）。或者说会离观察点越来越远。或者使用-1和-3的中间点-2应用Mpersp->ortho矩阵运算也会得到z变小的结果（带入其他特殊点运算也可，0~-1会不一样）。

下一节：计算机图形学-光栅化（三角形的离散化）_苏剑涛@XM的博客-CSDN博客