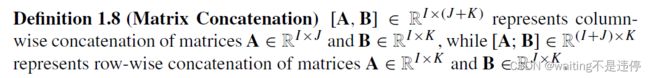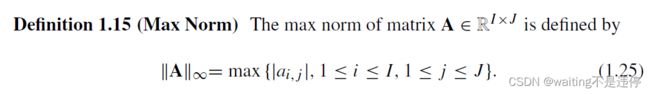1.2 python tensorly matrix矩阵基本操作

参考的书籍为Tensor Computation for Data Analysis
import

import numpy as np
import tensorly as tl
import 
tl.set_backend('numpy')

创建张量

a1 = np.array([[[1,3],[6,7]],[[3,5],[0,2]],[[6,4],[3,7]]])
t1 = tl.tensor(a1)
t1 = tl.tensor(np.arange(24).reshape((3, 4, 2)))

切片和fiber操作：和numpy一样，注意索引从0开始

t1[0,:,:]
t1[0,1,:]

定义1.2 Diagonal Tensor

order = 4
t2 = tl.tensor(np.zeros(tuple([order]*order)))
a2 = np.array([1,3,5,7])
for i in range(order):
    t2[tuple([i]*order)] = a2[i]

定义1.3 求矩阵的迹

a3 = np.arange(16).reshape((4, -1))
tr3 = np.trace(a3)

定义1.4 矩阵内积和张量内积，不能用np.inner，它会变成[email protected]，是矩阵乘法了

a4 = np.arange(6).reshape((3, -1))
a5 = np.arange(6).reshape((3, -1))
inner = tl.tenalg.inner(a3,a4)

定义1.5 Frobenius Norm

a4 = np.arange(6).reshape((3, -1))
a5 = np.arange(6).reshape((3, -1))
Frobenius = np.sqrt(tl.tenalg.inner(a3,a4))

定义1.6 Vector Outer Product

numpy和tensorly都可以实现

v1 = np.arange(5)
v2 = np.arange(5,10)
vouter = np.multiply.outer(v1,v2)
vouter = tl.tenalg.outer((v1,v2))

三个及以上的向量外积：

v1 = np.arange(5)
v2 = np.arange(5,10)
v3 = np.arange(1,3)
vouter3 = np.einsum('i,j,k->ijk',v1,v2,v3)

CP分解形式的外积也可以这么算：

X
fac_mat_list = []
X_pred = tl.fold(fac_mat_list[0]@tl.tenalg.khatri_rao(fac_mat_list,skip_matrix = 0).T,mode=0,shape=X.shape)

定义1.7 Hadamard Product

用numpy自带的*

a1 = np.arange(6).reshape((3, -1))
a2 = np.arange(6,12).reshape((3, -1))
Hadamard = a1*a2

定义1.8 Matrix Concatenation)

a1 = np.arange(6).reshape((3, -1))
a2 = np.arange(6,12).reshape((3, -1))
# [A;B]
Concatenation1 = np.concatenate((a1,a2),axis=0)

其它维度的也可以设置

a1 = np.arange(6).reshape((-1, 3))
a2 = np.arange(6,12).reshape((-1, 3))
# [A,B]
Concatenation2 = np.concatenate((a1,a2),axis=1)

注意，如果矩阵有mask，需要使用ma.concatenate

定义1.9 Kronecker Product

a1 = np.arange(6).reshape((-1, 3))
a2 = np.arange(6,12).reshape((-1, 3))
Kronecker = tl.tenalg.kronecker((a1,a2))

定理1.1

式1.9验证，看元素关系即可得

AkB = tl.tenalg.kronecker((A,B))
AkBkC1 = tl.tenalg.kronecker((AkB,C))

BkC = tl.tenalg.kronecker((B,C))
AkBkC2 = tl.tenalg.kronecker((AkB,C))

式1.10验证，从维度的角度也可以说得通

AC = A@C
BD = B@D
ACkBD = tl.tenalg.kronecker((AC,BD))

AkB = tl.tenalg.kronecker((A,B))
CkD = tl.tenalg.kronecker((C,D))
AkBCkD = AkB@CkD

式1.11，比对元素即可

AkCT = tl.tenalg.kronecker((A,C)).T
ATkCT = tl.tenalg.kronecker((A.T,C.T))

式1.12是伪逆矩阵，dagger符号。没有看证明，验证可以直接用
伪逆矩阵的定义

AkCP = tl.tenalg.kronecker((A,C))
AkCP = np.linalg.pinv(AkCP)

APkCP = tl.tenalg.kronecker((np.linalg.pinv(A),np.linalg.pinv(C)))

式1.13非常常见，需要记牢
向量化，vectorization定义如下

不能用reshape！！！！！

X = X.flatten('F')

式1.13的验证

A = np.arange(4).reshape(2,-1)
B = np.arange(4,8).reshape(2,-1)
C = np.arange(8,12).reshape(2,-1)
vABC = (A@B@C).flatten('F')
CtkAvB = tl.tenalg.kronecker((C.T, A))@B.flatten('F')

其证明在Tensor Decomposition for Signal Processing and Machine Learning这篇文章里，最后一步是对BkA的每列线性叠加

该式子可以用于求解如下问题

定义1.10 Khatri-Rao Product,和克罗内克积不同，它只续了列，而不是整个矩阵

A = np.array([[2,6],[2,1]])
B = np.array([[1,5],[3,8]])

AkrB = tl.tenalg.khatri_rao((A,B))
AkrB = tl.tenalg.khatri_rao([A,B])

定理1.2

定义所用到的矩阵值

A = np.array([[2,6],[2,1]])
B = np.array([[1,5],[3,8]])
C = np.arange(4).reshape(2,-1)
d = np.array([4,5])
D = np.diag(d)

式1.15，看索引可得

AkrBkrC1 = tl.tenalg.khatri_rao([A,B,C])
BkrC = tl.tenalg.khatri_rao([B,C])
AkrBkrC2 = tl.tenalg.khatri_rao([A,BkrC])

式1.16，菊花积学名叫Hadamard or element-wise product

AkrBtAkrB = tl.tenalg.khatri_rao([A,B]).T@tl.tenalg.khatri_rao([A,B])
AtAhBtB = (A.T@A)*(B.T@B)

式1.17

AkBCkrD = tl.tenalg.kronecker([A, B])@tl.tenalg.khatri_rao([C,D])
ACkrBD = tl.tenalg.khatri_rao([A@C,B@D])

式1.18

vADC = (A@D@C).flatten('F')
CtkrAd = tl.tenalg.khatri_rao([C.T,A])@d

定义1.11 Convolution卷积
Kn = In+Jn-1是因为要padding 0，padding的数量为Jn-1
k1-j1+1的+1是因为索引要从1开始，因此在python中不需要加


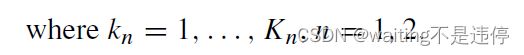
这个定义很bad，后面再搞

A = np.arange(25).reshape(5,-1)
[I1, I2] = A.shape
B = np.arange(9).reshape(3,-1)
[J1, J2] = B.shape
K1 = I1+J1-1
K2 = I2+J2-1
C = np.zeros((K1, K2))
# padding
A = np.concatenate((np.zeros((J1//2,I2)),A,np.zeros((J1//2,I2))),axis=0)
A = np.concatenate((np.zeros((I1+2*(J1//2),J2//2)),A,np.zeros((I1+2*(J1//2),J2//2))),axis=1)

for k1 in range(K1):
    for k2 in range(K2):
        for j1 in range(J1):
            for j2 in range(J2):
                C[k1,k2] += B[j1,j2]*A[k1-j1+1, k2-j2+1]

定义1.13 l norm，L范数

A = np.array([[0,6],[2,1]])
l1 = tl.norm(A,order=1)
l2 = tl.norm(A,order=2)
linf = tl.norm(A,order='inf')

l0 = np.linalg.norm(A.flatten(),ord=0)
linf = np.linalg.norm(A,ord=np.inf)

定义1.14 Off-diagonal l1 Norm

没有现成的，就自己造

l1off = tl.norm(A,order=1)-np.trace(A)

定义1.15 Max Norm

linf = tl.norm(A,order='inf')
linf = np.linalg.norm(A,ord=np.inf)

定义1.16 Nuclear Norm

lnuc = np.linalg.norm(A,ord='nuc')