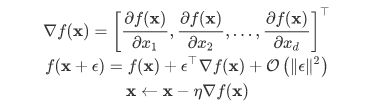DL基于Pytorch Day6 梯度下降

梯度下降

（Boyd & Vandenberghe, 2004）

%matplotlib inline
import numpy as np
import torch
import time
from torch import nn, optim
import math
import sys
sys.path.append('/home/kesci/input')
import d2lzh1981 as d2l

一维梯度下降

证明：沿梯度反方向移动自变量可以减小函数值

泰勒展开：

$f(x+ϵ)=f(x)+ϵf\prime (x)+O(ϵ2)$
代入沿梯度方向的移动量$ ηf′(x)$：

$f(x-\eta f\prime (x))=f(x)-\eta f\prime 2(x)+O(\eta 2f\prime 2(x))$
$f(x-\eta f\prime (x))\lesssim f(x)$
$x\leftarrow x-\eta f\prime (x)$
e.g.
$f(x)=x^2$

def f(x):
    return x**2  # Objective function

def gradf(x):
    return 2 * x  # Its derivative

def gd(eta):
    x = 10
    results = [x]
    for i in range(10):
        x -= eta * gradf(x)
        results.append(x)
    print('epoch 10, x:', x)
    return results

res = gd(0.2)
epoch 10, x: 0.06046617599999997
In [3]:
def show_trace(res):
    n = max(abs(min(res)), abs(max(res)))
    f_line = np.arange(-n, n, 0.01)
    d2l.set_figsize((3.5, 2.5))
    d2l.plt.plot(f_line, [f(x) for x in f_line],'-')
    d2l.plt.plot(res, [f(x) for x in res],'-o')
    d2l.plt.xlabel('x')
    d2l.plt.ylabel('f(x)')
    

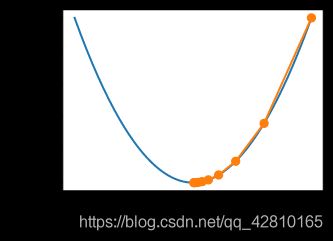
show_trace(res)

学习率

show_trace(gd(0.05))
epoch 10, x: 3.4867844009999995

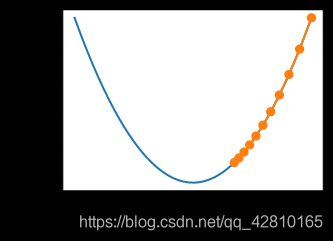
show_trace(gd(1.1))
epoch 10, x: 61.917364224000096

局部极小值

e.g.

$f(x)=xcoscx$

c = 0.15 * np.pi

def f(x):
    return x * np.cos(c * x)

def gradf(x):
    return np.cos(c * x) - c * x * np.sin(c * x)

show_trace(gd(2))
epoch 10, x: -1.528165927635083

多维梯度下降

def train_2d(trainer, steps=20):
    x1, x2 = -5, -2
    results = [(x1, x2)]
    for i in range(steps):
        x1, x2 = trainer(x1, x2)
        results.append((x1, x2))
    print('epoch %d, x1 %f, x2 %f' % (i + 1, x1, x2))
    return results

def show_trace_2d(f, results): 
    d2l.plt.plot(*zip(*results), '-o', color='#ff7f0e')
    x1, x2 = np.meshgrid(np.arange(-5.5, 1.0, 0.1), np.arange(-3.0, 1.0, 0.1))
    d2l.plt.contour(x1, x2, f(x1, x2), colors='#1f77b4')
    d2l.plt.xlabel('x1')
    d2l.plt.ylabel('x2')

$f(x)=x_2^1+2x_2^2$

eta = 0.1

def f_2d(x1, x2):  # 目标函数
    return x1 ** 2 + 2 * x2 ** 2

def gd_2d(x1, x2):
    return (x1 - eta * 2 * x1, x2 - eta * 4 * x2)

show_trace_2d(f_2d, train_2d(gd_2d))
epoch 20, x1 -0.057646, x2 -0.000073

自适应方法

牛顿法

在 x+ϵ 处泰勒展开：

最小值点处满足: ∇f(x)=0, 即我们希望 ∇f(x+ϵ)=0, 对上式关于 ϵ 求导，忽略高阶无穷小，有：

c = 0.5

def f(x):
    return np.cosh(c * x)  # Objective

def gradf(x):
    return c * np.sinh(c * x)  # Derivative

def hessf(x):
    return c**2 * np.cosh(c * x)  # Hessian

#Hide learning rate for now
def newton(eta=1):
    x = 10
    results = [x]
    for i in range(10):
        x -= eta * gradf(x) / hessf(x)
        results.append(x)
    print('epoch 10, x:', x)
    return results

show_trace(newton())
#epoch 10, x: 0.0

In [10]:
c = 0.15 * np.pi

def f(x):
    return x * np.cos(c * x)

def gradf(x):
    return np.cos(c * x) - c * x * np.sin(c * x)

def hessf(x):
    return - 2 * c * np.sin(c * x) - x * c**2 * np.cos(c * x)

show_trace(newton())
#epoch 10, x: 26.83413291324767


show_trace(newton(0.5))
#epoch 10, x: 7.269860168684531

收敛性分析

预处理 （Heissan阵辅助梯度下降）

$x\leftarrow x-\eta diag(Hf{)}^{-1}\nabla x$

随机梯度下降

随机梯度下降参数更新

对于有 n 个样本对训练数据集，设 fi(x) 是第 i 个样本的损失函数, 则目标函数为:

其梯度为:

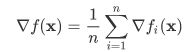
使用该梯度的一次更新的时间复杂度为 O(n)
随机梯度下降更新公式 O(1):

$x\leftarrow x-\eta \nabla f_i(x)$
且有：

e.g.

$f(x1,x2)=x_2^1+2x_2^2$

def f(x1, x2):
    return x1 ** 2 + 2 * x2 ** 2  # Objective

def gradf(x1, x2):
    return (2 * x1, 4 * x2)  # Gradient

def sgd(x1, x2):  # Simulate noisy gradient
    global lr  # Learning rate scheduler
    (g1, g2) = gradf(x1, x2)  # Compute gradient
    (g1, g2) = (g1 + np.random.normal(0.1), g2 + np.random.normal(0.1))
    eta_t = eta * lr()  # Learning rate at time t
    return (x1 - eta_t * g1, x2 - eta_t * g2)  # Update variables

eta = 0.1
lr = (lambda: 1)  # Constant learning rate
show_trace_2d(f, train_2d(sgd, steps=50))
#epoch 50, x1 -0.027566, x2 0.137605

动态学习率

def exponential():
    global ctr
    ctr += 1
    return math.exp(-0.1 * ctr)

ctr = 1
lr = exponential  # Set up learning rate
show_trace_2d(f, train_2d(sgd, steps=1000))
epoch 1000, x1 -0.677947, x2 -0.089379


def polynomial():
    global ctr
    ctr += 1
    return (1 + 0.1 * ctr)**(-0.5)

ctr = 1
lr = polynomial  # Set up learning rate
show_trace_2d(f, train_2d(sgd, steps=50))
#epoch 50, x1 -0.095244, x2 -0.041674

小批量随机梯度下降

读取数据

def get_data_ch7():  # 本函数已保存在d2lzh_pytorch包中方便以后使用
    data = np.genfromtxt('/home/kesci/input/airfoil4755/airfoil_self_noise.dat', delimiter='\t')
    data = (data - data.mean(axis=0)) / data.std(axis=0) # 标准化
    return torch.tensor(data[:1500, :-1], dtype=torch.float32), \
           torch.tensor(data[:1500, -1], dtype=torch.float32) # 前1500个样本(每个样本5个特征)

features, labels = get_data_ch7()
features.shape
Out[16]:
torch.Size([1500, 5])
In [17]:
import pandas as pd
df = pd.read_csv('/home/kesci/input/airfoil4755/airfoil_self_noise.dat', delimiter='\t', header=None)
df.head(10)
#Out
0	1	2	3	4	5
0	800	0.0	0.3048	71.3	0.002663	126.201
1	1000	0.0	0.3048	71.3	0.002663	125.201
2	1250	0.0	0.3048	71.3	0.002663	125.951
3	1600	0.0	0.3048	71.3	0.002663	127.591
4	2000	0.0	0.3048	71.3	0.002663	127.461
5	2500	0.0	0.3048	71.3	0.002663	125.571
6	3150	0.0	0.3048	71.3	0.002663	125.201
7	4000	0.0	0.3048	71.3	0.002663	123.061
8	5000	0.0	0.3048	71.3	0.002663	121.301
9	6300	0.0	0.3048	71.3	0.002663	119.541

简洁实现

#本函数与原书不同的是这里第一个参数优化器函数而不是优化器的名字
#例如: optimizer_fn=torch.optim.SGD, optimizer_hyperparams={"lr": 0.05}
def train_pytorch_ch7(optimizer_fn, optimizer_hyperparams, features, labels,
                    batch_size=10, num_epochs=2):
    # 初始化模型
    net = nn.Sequential(
        nn.Linear(features.shape[-1], 1)
    )
    loss = nn.MSELoss()
    optimizer = optimizer_fn(net.parameters(), **optimizer_hyperparams)

    def eval_loss():
        return loss(net(features).view(-1), labels).item() / 2

    ls = [eval_loss()]
    data_iter = torch.utils.data.DataLoader(
        torch.utils.data.TensorDataset(features, labels), batch_size, shuffle=True)

    for _ in range(num_epochs):
        start = time.time()
        for batch_i, (X, y) in enumerate(data_iter):
            # 除以2是为了和train_ch7保持一致, 因为squared_loss中除了2
            l = loss(net(X).view(-1), y) / 2 
            
            optimizer.zero_grad()
            l.backward()
            optimizer.step()
            if (batch_i + 1) * batch_size % 100 == 0:
                ls.append(eval_loss())
    # 打印结果和作图
    print('loss: %f, %f sec per epoch' % (ls[-1], time.time() - start))
    d2l.set_figsize()
    d2l.plt.plot(np.linspace(0, num_epochs, len(ls)), ls)
    d2l.plt.xlabel('epoch')
    d2l.plt.ylabel('loss')
In [25]:
train_pytorch_ch7(optim.SGD, {"lr": 0.05}, features, labels, 10)
#loss: 0.243770, 0.047664 sec per epoch