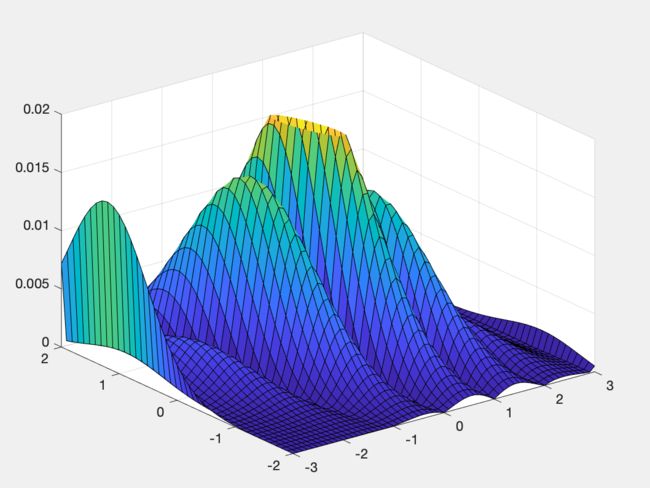
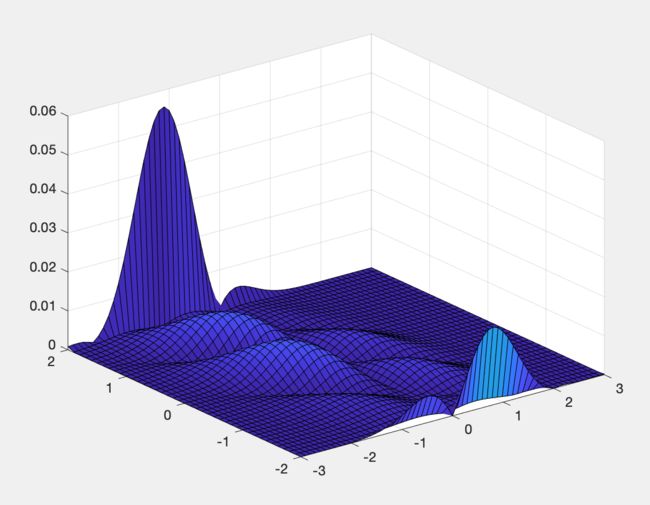
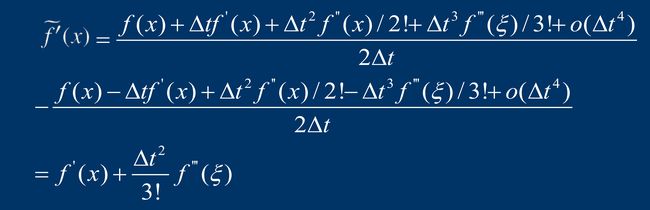基于MATLAB的数值微分与拟合多项式求导
目录
前言
一. 数值微分算法
中心公式一：
中心公式二：
二. 中心差分算法及其MATLAB的实现方法
例题一
三. 用插值、拟合多项式求导数
例题二
四. 二元函数的梯度计算
前言
由导数的定义得：
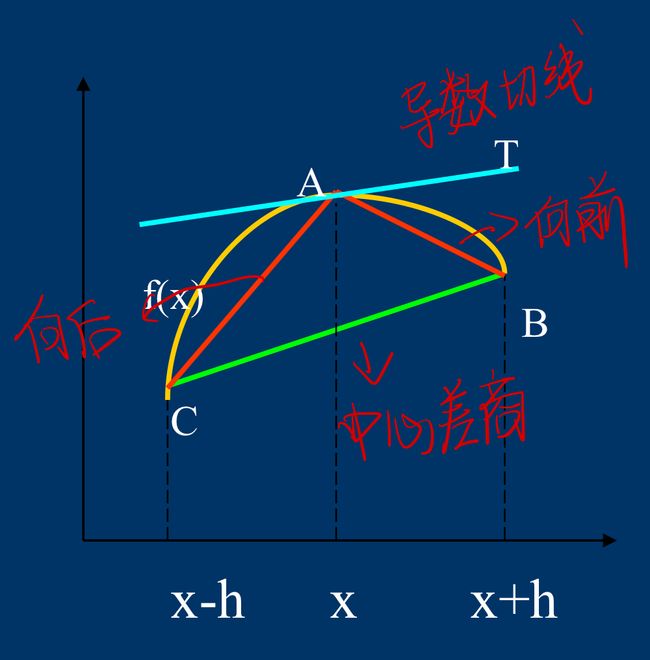
进行细化区分为三种：
（1）向前差商公式:
（2）向后差商公式：
（3）利用中点方法的中心差商公式：
将导数的几何性质对应于曲线在某点处的切线，形成如下图的理解：
一. 数值微分算法
向前差商公式：
向后差商公式：
这两种算法的精度都为
。具体理解可参照计算复杂性的内容。此两种算法结构简单，以下把重心转移到中心公式。
中心公式一：
对应的函数近似求微分为
。接着对此式子利用Taylor级数展开为如下：
由以上结果可以发现算法精度为
。
有关MATLAB与Taylor幂级数展开有关的内容，可以查看此专栏：
CSDN
二阶，三阶，四阶等高阶微分公式也可类推计算如下：
二阶微分：
三阶微分：
四阶微分：
中心公式二：
此算法精度为
。具体证明过程参照计算复杂性内容，此处略。
一阶，二阶，三阶，四阶等高阶微分公式也可类推计算如下【证明过程此处略】：
一阶微分：
二阶微分：
三阶微分：
四阶微分：
二. 中心差分算法及其MATLAB的实现方法
首先需要定义一个中心差分函数，如下：
function [dy,dx]=diff_ctr(y,Dt,n)
yx1=[y 0 0 0 0 0]; yx2=[0 y 0 0 0 0]; yx3=[0 0 y 0 0 0];
yx4=[0 0 0 y 0 0]; yx5=[0 0 0 0 y 0]; yx6=[0 0 0 0 0 y];
switch n
case 1
dy=(-diff(yx1)+7*diff(yx2)+7*diff(yx3)-diff(yx4))/(12*Dt); L0=3;
case 2
dy=(-diff(yx1)+15*diff(yx2)- 15*diff(yx3)+diff(yx4))/(12*Dt^2); L0=3;
case 3
dy=(-diff(yx1)+7*diff(yx2)-6*diff(yx3)-6*diff(yx4)+...
7*diff(yx5)-diff(yx6))/(8*Dt^3); L0=5;
case 4
dy = (-diff(yx1)+11*diff(yx2)-28*diff(yx3)+28*...
diff(yx4)-11*diff(yx5)+diff(yx6))/(6*Dt^4); L0=5;
end
dy=dy(L0+1:end-L0); dx=([1:length(dy)]+L0-2-(n>2))*Dt;
end根据此定义的函数，在MATLAB中调用的格式：
[dy,dx]=diff_ctr(y,
t,n)
y为等距实测的数据，dy为得出的导数向量，dx为相应的自变量向量。且dy,dx的数据比y短。
例题一
已知 
，求导数的解析解，再用数值微分求取原函数的1~4阶导数，并和解析解比较精度。
代码如下：
clc;clear;
h=0.05;
x=0:h:pi;
syms x1;
y=sin(x1)/(x1^2+4*x1+3);
%求各阶导数的解析解与对照数据
yy1=diff(y); f1=subs(yy1,x1,x);
yy2=diff(yy1); f2=subs(yy2,x1,x);
yy3=diff(yy2); f3=subs(yy3,x1,x);
yy4=diff(yy3); f4=subs(yy4,x1,x);
y=sin(x)./(x.^2+4*x+3); %生成已知数据点
[y1,dx1]=diff_ctr(y,h,1);subplot(221),plot(x,f1,dx1,y1,':');
[y2,dx2]=diff_ctr(y,h,2);subplot(222),plot(x,f2,dx2,y2,':');
[y3,dx3]=diff_ctr(y,h,3);subplot(223),plot(x,f3,dx3,y3,':');
[y4,dx4]=diff_ctr(y,h,4);subplot(224),plot(x,f4,dx4,y4,':');
%以四阶导数为例子比较精度，求最大相对误差误差
vpa(norm((y4-f4(4:60))./f4(4:60)))
function [dy,dx]=diff_ctr(y,Dt,n)
yx1=[y 0 0 0 0 0]; yx2=[0 y 0 0 0 0]; yx3=[0 0 y 0 0 0];
yx4=[0 0 0 y 0 0]; yx5=[0 0 0 0 y 0]; yx6=[0 0 0 0 0 y];
switch n
case 1
dy=(-diff(yx1)+7*diff(yx2)+7*diff(yx3)-diff(yx4))/(12*Dt); L0=3;
case 2
dy=(-diff(yx1)+15*diff(yx2)- 15*diff(yx3)+diff(yx4))/(12*Dt^2); L0=3;
case 3
dy=(-diff(yx1)+7*diff(yx2)-6*diff(yx3)-6*diff(yx4)+...
7*diff(yx5)-diff(yx6))/(8*Dt^3); L0=5;
case 4
dy = (-diff(yx1)+11*diff(yx2)-28*diff(yx3)+28*...
diff(yx4)-11*diff(yx5)+diff(yx6))/(6*Dt^4); L0=5;
end
dy=dy(L0+1:end-L0); dx=([1:length(dy)]+L0-2-(n>2))*Dt;
end
运行结果：
ans =0.00035025290663255084830847352436447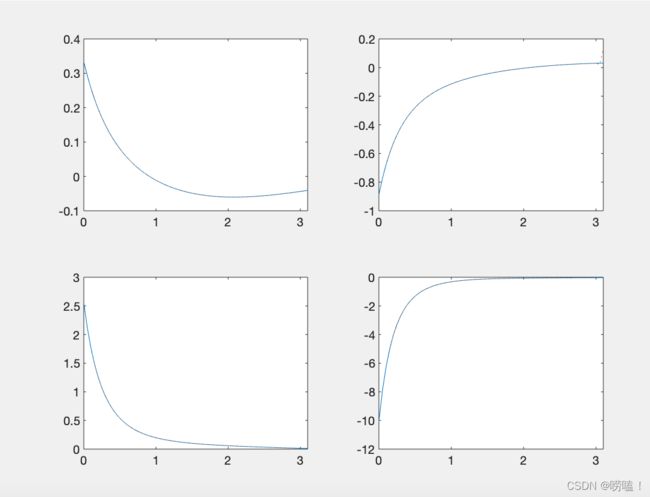 
说明：运行图像说明两者几乎重合，"ans"结果说明相对误差很小，到小数点后四位。
三. 用插值、拟合多项式求导数
基本思想：当已知函数在一些离散点上的函数值时，该函数可用插值或拟合多项式来近似，然后对多项式进行微分求得导数。
步骤一：选取x=0附近的少量点
步骤二：进行多项式拟合或插值
步骤三：g(x)在x=0处k阶导数为：
原函数和该拟合多项式的运算满足如下式子：
通过坐标变换用上述方法可计算任意x点处的导数值。
将
代入
中，将g(x)改写为关于z的表达式：
导函数可计算为：
可以直接用
拟合节点
得到系数
。MATLAB代码如下：
d=polyfit(x-a,y,length(xd)-1)
d=polyfit(x-a,y,length(x)-1)例题二
某数据集合如下：
| xd | 0 | 0.2000 | 0.4000 | 0.6000 | 0.8000 | 1.000 |
| yd | 0.3927 | 0.5672 | 0.6982 | 0.7941 | 0.8614 | 0.9053 |
计算x=a=0.3处的各阶导数。
解：
代码如下：
clc;clear;
xd=[0 0.2000 0.4000 0.6000 0.8000 1.000];
yd=[0.3927 0.5672 0.6982 0.7941 0.8614 0.9053];
a=0.3;
L=length(xd);
d=polyfit(xd-a,yd,L-1);fact=[1];
for k=1:L-1;
fact=[factorial(k),fact];
end
deriv=d.*fact输出的结果：
deriv =
1.875000000002103 -1.375000000000392 1.040624999999999 -0.971041666666661 0.653264062500000 0.637560937500000
四. 二元函数的梯度计算
二元函数的函数值矩阵z为网格数据，计算z如下：
若z矩阵是建立在等间距的形式生成的网格基础上，则实际梯度可计算为：
上式子中，
和
分别为x,y生成网格的步距。
例题3
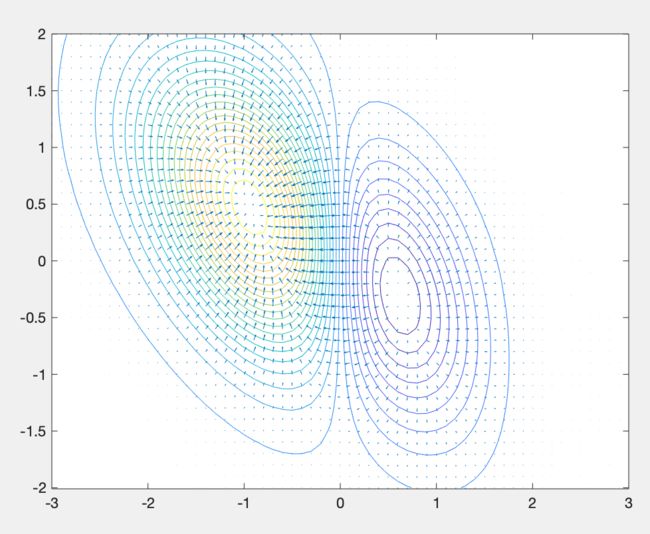
计算梯度，绘制引力线图：
解：
MATLAB代码：
clc;clear;
[x,y]=meshgrid(-3:.1:3,-2:.1:2);
z=(x.^2-2*x).*exp(-x.^2-y.^2-x.*y);
[fx,fy]=gradient(z);
fx=fx/0.1;
fy=fy/0.1;
%绘制等高线与引力线图
contour(x,y,z,30);
hold on;
quiver(x,y,fx,fy)
%绘制误差曲面
zx=-exp(-x.^2-y.^2-x.*y).*(-2*x+2+2*x.^3+x.^2.*y-4*x.^2-2*x.*y);
zy=-x.*(x-2).*(2*y+x).*exp(-x.^2-y.^2-x.*y);
figure
surf(x,y,abs(fx-zx)); axis([-3 3 -2 2 0,0.02])
figure;
surf(x,y,abs(fy-zy)); axis([-3 3 -2 2 0,0.06])运行结果：
