强化学习（实践）：DQN，Double DQN，Dueling DQN，格子环境

1，DQN算法

1.1，CarPole环境

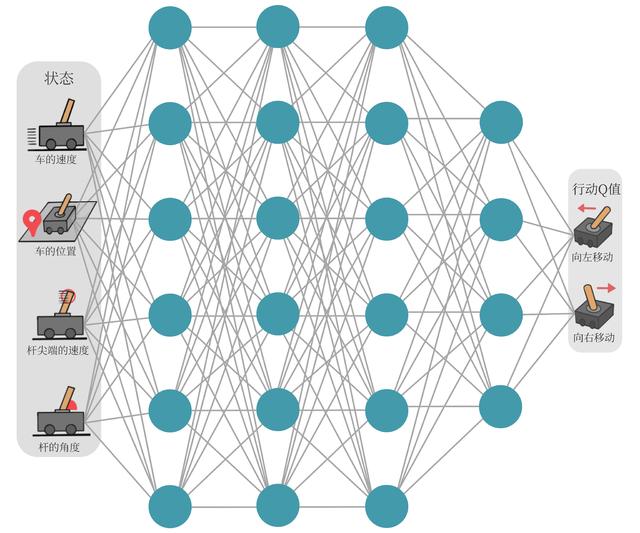
以车杆（CartPole）环境为例，它的状态值就是连续的，动作值是离散的。在车杆环境中，有一辆小车，智能体的任务是通过左右移动保持车上的杆竖直，若杆的倾斜度数过大，或者车子离初始位置左右的偏离程度过大，或者坚持时间到达 200 帧，则游戏结束。智能体的状态是一个维数为 4 的向量，每一维都是连续的，其动作是离散的，动作空间大小为 2，详情参见表 7-1 和表 7-2。在游戏中每坚持一帧，智能体能获得分数为 1 的奖励，坚持时间越长，则最后的分数越高，坚持 200 帧即可获得最高的分数。

状态空间：

维度	意义	最小值	最大值
0	车的位置	-2.4	2.4
1	车的速度	-Inf	Inf
2	杆的角度	~ -41.8°	~ 41.8°
3	杆尖端的速度	-Inf	Inf

动作空间：

标号	动作
0	向左移动小车
1	向右移动小车

1.2，DQN原理

现在我们想在类似车杆的环境中得到动作价值函数 ，由于状态每一维度的值都是连续的，无法使用表格记录，因此一个常见的解决方法便是使用函数拟合（function approximation）的思想。由于神经网络具有强大的表达能力，因此我们可以用一个神经网络来表示函数 。

• 若动作是连续（无限）的，神经网络的输入是状态  和动作 ，然后输出一个标量，表示在状态  下采取动作  能获得的价值。
• 若动作是离散（有限）的，除了可以采取动作连续情况下的做法，我们还可以只将状态  输入到神经网络中，使其同时输出每一个动作的  值。

通常 DQN（以及 Q-learning）只能处理动作离散的情况，因为在函数  的更新过程中有  这一操作。假设神经网络用来拟合函数的参数是 ，即每一个状态  下所有可能动作  的值我们都能表示为 。我们将用于拟合函数  函数的神经网络称为Q 网络。

1.3，DQN实现

rl_utils库：它包含一些专门的函数，如绘制移动平均曲线、计算优势函数等，不同的算法可以一起使用这些函数。

from tqdm import tqdm
import numpy as np
import torch
import collections
import random

class ReplayBuffer:
    def __init__(self, capacity):
        self.buffer = collections.deque(maxlen=capacity)

    def add(self, state, action, reward, next_state, done):
        self.buffer.append((state, action, reward, next_state, done))

    def sample(self, batch_size):
        transitions = random.sample(self.buffer, batch_size)
        state, action, reward, next_state, done = zip(*transitions)
        return np.array(state), action, reward, np.array(next_state), done

    def size(self):
        return len(self.buffer)

def moving_average(a, window_size):
    cumulative_sum = np.cumsum(np.insert(a, 0, 0))
    middle = (cumulative_sum[window_size:] - cumulative_sum[:-window_size]) / window_size
    r = np.arange(1, window_size - 1, 2)
    begin = np.cumsum(a[:window_size - 1])[::2] / r
    end = (np.cumsum(a[:-window_size:-1])[::2] / r)[::-1]
    return np.concatenate((begin, middle, end))

def train_on_policy_agent(env, agent, num_episodes):
    return_list = []
    for i in range(10):
        with tqdm(total=int(num_episodes / 10), desc='Iteration %d' % i) as pbar:
            for i_episode in range(int(num_episodes / 10)):
                episode_return = 0
                transition_dict = {'states': [], 'actions': [], 'next_states': [], 'rewards': [], 'dones': []}
                state = env.reset()
                done = False
                while not done:
                    action = agent.take_action(state)
                    next_state, reward, done, _ = env.step(action)
                    transition_dict['states'].append(state)
                    transition_dict['actions'].append(action)
                    transition_dict['next_states'].append(next_state)
                    transition_dict['rewards'].append(reward)
                    transition_dict['dones'].append(done)
                    state = next_state
                    episode_return += reward
                return_list.append(episode_return)
                agent.update(transition_dict)
                if (i_episode + 1) % 10 == 0:
                    pbar.set_postfix({'episode': '%d' % (num_episodes / 10 * i + i_episode + 1),
                                      'return': '%.3f' % np.mean(return_list[-10:])})
                pbar.update(1)
    return return_list

def train_off_policy_agent(env, agent, num_episodes, replay_buffer, minimal_size, batch_size):
    return_list = []
    for i in range(10):
        with tqdm(total=int(num_episodes / 10), desc='Iteration %d' % i) as pbar:
            for i_episode in range(int(num_episodes / 10)):
                episode_return = 0
                state = env.reset()
                done = False
                while not done:
                    action = agent.take_action(state)
                    next_state, reward, done, _ = env.step(action)
                    replay_buffer.add(state, action, reward, next_state, done)
                    state = next_state
                    episode_return += reward
                    if replay_buffer.size() > minimal_size:
                        b_s, b_a, b_r, b_ns, b_d = replay_buffer.sample(batch_size)
                        transition_dict = {'states': b_s, 'actions': b_a, 'next_states': b_ns, 'rewards': b_r,
                                           'dones': b_d}
                        agent.update(transition_dict)
                return_list.append(episode_return)
                if (i_episode + 1) % 10 == 0:
                    pbar.set_postfix({'episode': '%d' % (num_episodes / 10 * i + i_episode + 1),
                                      'return': '%.3f' % np.mean(return_list[-10:])})
                pbar.update(1)
    return return_list

def compute_advantage(gamma, lmbda, td_delta):
    td_delta = td_delta.detach().numpy()
    advantage_list = []
    advantage = 0.0
    for delta in td_delta[::-1]:
        advantage = gamma * lmbda * advantage + delta
        advantage_list.append(advantage)
    advantage_list.reverse()
    return torch.tensor(advantage_list, dtype=torch.float)

首先定义经验回放池的类，主要包括加入数据、采样数据两大函数。

import random
import gym
import numpy as np
import collections
from tqdm import tqdm
import torch
import torch.nn.functional as F
import matplotlib.pyplot as plt
class ReplayBuffer:
    ''' 经验回放池 '''
    def __init__(self, capacity):
        self.buffer = collections.deque(maxlen=capacity)  # 队列,先进先出

    def add(self, state, action, reward, next_state, done):  # 将数据加入buffer
        self.buffer.append((state, action, reward, next_state, done))

    def sample(self, batch_size):  # 从buffer中采样数据,数量为batch_size
        transitions = random.sample(self.buffer, batch_size)
        state, action, reward, next_state, done = zip(*transitions)
        return np.array(state), action, reward, np.array(next_state), done

    def size(self):  # 目前buffer中数据的数量
        return len(self.buffer)

然后定义一个只有一层隐藏层的 Q 网络。

class Qnet(torch.nn.Module):
    ''' 只有一层隐藏层的Q网络 '''
    def __init__(self, state_dim, hidden_dim, action_dim):
        super(Qnet, self).__init__()
        self.fc1 = torch.nn.Linear(state_dim, hidden_dim)
        self.fc2 = torch.nn.Linear(hidden_dim, action_dim)

    def forward(self, x):
        x = F.relu(self.fc1(x))  # 隐藏层使用ReLU激活函数
        return self.fc2(x)

有了这些基本组件之后，接来下开始实现 DQN 算法。

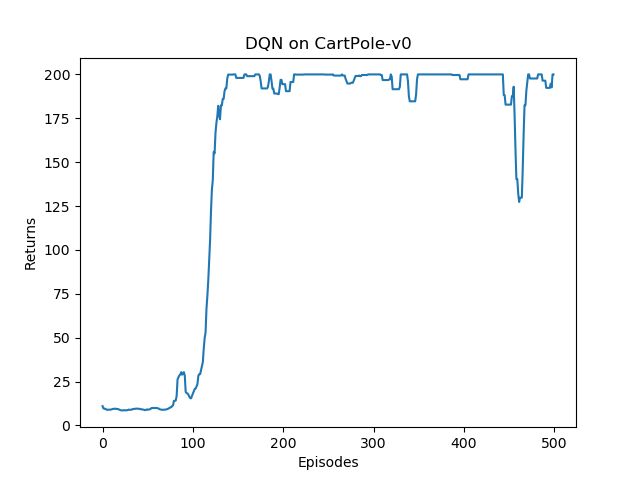
class DQN:
    ''' DQN算法 '''
    def __init__(self, state_dim, hidden_dim, action_dim, learning_rate, gamma,epsilon, target_update, device):
        self.action_dim = action_dim
        self.q_net = Qnet(state_dim, hidden_dim, self.action_dim).to(device)  # Q网络
        # 目标网络
        self.target_q_net = Qnet(state_dim, hidden_dim, self.action_dim).to(device)
        # 使用Adam优化器
        self.optimizer = torch.optim.Adam(self.q_net.parameters(), lr=learning_rate)
        self.gamma = gamma  # 折扣因子
        self.epsilon = epsilon  # epsilon-贪婪策略
        self.target_update = target_update  # 目标网络更新频率
        self.count = 0  # 计数器,记录更新次数
        self.device = device

    def take_action(self, state):  # epsilon-贪婪策略采取动作
        if np.random.random() < self.epsilon:
            action = np.random.randint(self.action_dim)
        else:
            state = torch.tensor([state], dtype=torch.float).to(self.device)
            action = self.q_net(state).argmax().item()
        return action

    def update(self, transition_dict):
        states = torch.tensor(transition_dict['states'], dtype=torch.float).to(self.device)
        actions = torch.tensor(transition_dict['actions']).view(-1, 1).to(self.device)
        rewards = torch.tensor(transition_dict['rewards'], dtype=torch.float).view(-1, 1).to(self.device)
        next_states = torch.tensor(transition_dict['next_states'], dtype=torch.float).to(self.device)
        dones = torch.tensor(transition_dict['dones'], dtype=torch.float).view(-1, 1).to(self.device)

        q_values = self.q_net(states).gather(1, actions)  # Q值
        # 下个状态的最大Q值
        max_next_q_values = self.target_q_net(next_states).max(1)[0].view(-1, 1)
        q_targets = rewards + self.gamma * max_next_q_values * (1 - dones)  # TD误差目标
        dqn_loss = torch.mean(F.mse_loss(q_values, q_targets))  # 均方误差损失函数
        self.optimizer.zero_grad()  # PyTorch中默认梯度会累积,这里需要显式将梯度置为0
        dqn_loss.backward()  # 反向传播更新参数
        self.optimizer.step()

        if self.count % self.target_update == 0:
            self.target_q_net.load_state_dict(
                self.q_net.state_dict())  # 更新目标网络
        self.count += 1

lr = 2e-3
num_episodes = 500
hidden_dim = 128
gamma = 0.98
epsilon = 0.01
target_update = 10
buffer_size = 10000
minimal_size = 500
batch_size = 64
device = torch.device("cuda") if torch.cuda.is_available() else torch.device("cpu")

env_name = 'CartPole-v1'
env = gym.make(env_name)
random.seed(0)
np.random.seed(0)
env.seed(0)
torch.manual_seed(0)
replay_buffer = ReplayBuffer(buffer_size)
state_dim = env.observation_space.shape[0]
action_dim = env.action_space.n
agent = DQN(state_dim, hidden_dim, action_dim, lr, gamma, epsilon, target_update, device)

return_list = []
for i in range(10):
    with tqdm(total=int(num_episodes / 10), desc='Iteration %d' % i) as pbar:
        for i_episode in range(int(num_episodes / 10)):
            episode_return = 0
            state = env.reset()
            env.render()
            done = False
            while not done:
                action = agent.take_action(state)
                next_state, reward, done, _ = env.step(action)
                replay_buffer.add(state, action, reward, next_state, done)
                state = next_state
                episode_return += reward
                # 当buffer数据的数量超过一定值后,才进行Q网络训练
                if replay_buffer.size() > minimal_size:
                    b_s, b_a, b_r, b_ns, b_d = replay_buffer.sample(batch_size)
                    transition_dict = {
                        'states': b_s,
                        'actions': b_a,
                        'next_states': b_ns,
                        'rewards': b_r,
                        'dones': b_d
                    }
                    agent.update(transition_dict)
            return_list.append(episode_return)
            if (i_episode + 1) % 10 == 0:
                pbar.set_postfix({
                    'episode':
                    '%d' % (num_episodes / 10 * i + i_episode + 1),
                    'return':
                    '%.3f' % np.mean(return_list[-10:])
                })
            pbar.update(1)

Iteration 0: 100%|██████████| 50/50 [00:03<00:00, 13.68it/s, episode=50, return=9.000]
Iteration 1: 100%|██████████| 50/50 [00:02<00:00, 20.19it/s, episode=100, return=17.900]
Iteration 2: 100%|██████████| 50/50 [00:20<00:00,  2.41it/s, episode=150, return=199.900]
Iteration 3: 100%|██████████| 50/50 [00:31<00:00,  1.59it/s, episode=200, return=189.900]
Iteration 4: 100%|██████████| 50/50 [00:31<00:00,  1.56it/s, episode=250, return=200.000]
Iteration 5: 100%|██████████| 50/50 [00:31<00:00,  1.57it/s, episode=300, return=200.000]
Iteration 6: 100%|██████████| 50/50 [00:31<00:00,  1.61it/s, episode=350, return=186.200]
Iteration 7: 100%|██████████| 50/50 [00:32<00:00,  1.56it/s, episode=400, return=199.700]
Iteration 8: 100%|██████████| 50/50 [00:31<00:00,  1.58it/s, episode=450, return=189.400]
Iteration 9: 100%|██████████| 50/50 [00:29<00:00,  1.68it/s, episode=500, return=193.100]

episodes_list = list(range(len(return_list)))
plt.plot(episodes_list, return_list)
plt.xlabel('Episodes')
plt.ylabel('Returns')
plt.title('DQN on {}'.format(env_name))
plt.show()

mv_return = rl_utils.moving_average(return_list, 9)
plt.plot(episodes_list, mv_return)
plt.xlabel('Episodes')
plt.ylabel('Returns')
plt.title('DQN on {}'.format(env_name))
plt.show()

可以看到，DQN 的性能在 100 个序列后很快得到提升，最终收敛到策略的最优回报值 200。我们也可以看到，在 DQN 的性能得到提升后，它会持续出现一定程度的震荡，这主要是神经网络过拟合到一些局部经验数据后由  运算带来的影响。

1.4，图片输入

图片输入效果不是很好，因此大部分都是使用的非图片输入。

import collections

import gym
import math
import random
import numpy as np
import matplotlib
import matplotlib.pyplot as plt
from collections import namedtuple
from itertools import count
from PIL import Image
import torch
import torch.nn as nn
import torch.optim as optim
import torch.nn.functional as F
import torchvision.transforms as T

# env = gym.make('CartPole-v0').unwrapped
from tqdm import tqdm

is_ipython = 'inline' in matplotlib.get_backend()
if is_ipython:
    from IPython import display
plt.ion()
device = torch.device("cuda" if torch.cuda.is_available() else "cpu")
Transition = namedtuple('Transition', ('state', 'action', 'next_state', 'reward'))
resize = T.Compose([T.ToPILImage(), T.Resize(40, interpolation=Image.CUBIC), T.ToTensor()])

def moving_average(a, window_size):
    cumulative_sum = np.cumsum(np.insert(a, 0, 0))
    middle = (cumulative_sum[window_size:] - cumulative_sum[:-window_size]) / window_size
    r = np.arange(1, window_size - 1, 2)
    begin = np.cumsum(a[:window_size - 1])[::2] / r
    end = (np.cumsum(a[:-window_size:-1])[::2] / r)[::-1]
    return np.concatenate((begin, middle, end))

class ReplayBuffer:
    def __init__(self, capacity):
        self.buffer = collections.deque(maxlen=capacity)

    def add(self, state, action, reward, next_state):
        self.buffer.append((state, action, reward, next_state))

    def sample(self, batch_size):
        transitions = random.sample(self.buffer, batch_size)
        return transitions
    def size(self):
        return len(self.buffer)

class Qnet(nn.Module):
    def __init__(self, h, w, outputs):
        super(Qnet, self).__init__()
        self.conv1 = nn.Conv2d(3, 16, kernel_size=5, stride=2)
        self.bn1 = nn.BatchNorm2d(16)
        self.conv2 = nn.Conv2d(16, 32, kernel_size=5, stride=2)
        self.bn2 = nn.BatchNorm2d(32)
        self.conv3 = nn.Conv2d(32, 32, kernel_size=5, stride=2)
        self.bn3 = nn.BatchNorm2d(32)

        def conv2d_size_out(size, kernel_size=5, stride=2):
            return (size - (kernel_size - 1) - 1) // stride + 1

        convw = conv2d_size_out(conv2d_size_out(conv2d_size_out(w)))
        convh = conv2d_size_out(conv2d_size_out(conv2d_size_out(h)))
        linear_input_size = convw * convh * 32
        self.head = nn.Linear(linear_input_size, outputs)

    def forward(self, x):
        x = F.relu(self.bn1(self.conv1(x)))
        x = F.relu(self.bn2(self.conv2(x)))
        x = F.relu(self.bn3(self.conv3(x)))
        return self.head(x.view(x.size(0), -1))

class DQN:
    def __init__(self,gamma,epsilon):
        self.env = gym.make('CartPole-v0').unwrapped
        self.env.reset()
        self.init_screen = self.get_screen()
        _, _, self.screen_height, self.screen_width = self.init_screen.shape
        self.n_actions = self.env.action_space.n
        self.policy_net = Qnet(self.screen_height, self.screen_width, self.n_actions).to(device)
        self.target_net = Qnet(self.screen_height, self.screen_width, self.n_actions).to(device)
        self.target_net.load_state_dict(self.policy_net.state_dict())
        self.target_net.eval()
        self.optimizer = optim.RMSprop(self.policy_net.parameters())
        self.gamma = gamma  # 折扣因子
        self.epsilon = epsilon  # epsilon-贪婪策略

    def take_action(self, state):
        global steps_done
        sample = random.random()
        steps_done += 1
        if sample > self.epsilon:   # epsilon-贪婪策略采取动作
            with torch.no_grad():
                return self.policy_net(state).max(1)[1].view(1, 1)
        else:
            return torch.tensor([[random.randrange(self.n_actions)]], device=device, dtype=torch.long)

    def update(self, transitions):
        batch = Transition(*zip(*transitions))
        # 计算非最终状态的掩码并连接批处理元素(最终状态将是模拟结束后的状态）
        non_final_mask = torch.tensor(tuple(map(lambda s: s is not None, batch.next_state)), device=device,dtype=torch.bool)
        non_final_next_states = torch.cat([s for s in batch.next_state if s is not None])
        state_batch = torch.cat(batch.state)
        action_batch = torch.cat(batch.action)
        reward_batch = torch.cat(batch.reward)
        # 计算Q(s_t, a)-模型计算 Q(s_t)，然后选择所采取行动的列。
        # 这些是根据策略网络对每个批处理状态所采取的操作。
        state_action_values = self.policy_net(state_batch).gather(1, action_batch)
        # 计算下一个状态的V(s_{t+1})。
        # 非最终状态下一个状态的预期操作值是基于“旧”目标网络计算的；选择max(1)[0]的最佳奖励。
        # 这是基于掩码合并的，这样当状态为最终状态时，我们将获得预期状态值或0。
        next_state_values = torch.zeros(batch_size, device=device)
        next_state_values[non_final_mask] = self.target_net(non_final_next_states).max(1)[0].detach()
        # 计算期望Q值
        expected_state_action_values = (next_state_values * self.gamma) + reward_batch
        # 计算Huber损失
        loss = F.smooth_l1_loss(state_action_values, expected_state_action_values.unsqueeze(1))
        # 优化模型
        self.optimizer.zero_grad()
        loss.backward()
        self.optimizer.step()

        for param in self.policy_net.parameters():
            param.grad.data.clamp_(-1, 1)
    def get_cart_location(self, screen_width):
        world_width = self.env.x_threshold * 2
        scale = screen_width / world_width
        return int(self.env.state[0] * scale + screen_width / 2.0)  # MIDDLE OF CART

    def get_screen(self):
        screen = self.env.render(mode='rgb_array').transpose((2, 0, 1))
        _, screen_height, screen_width = screen.shape
        screen = screen[:, int(screen_height * 0.4):int(screen_height * 0.8)]
        view_width = int(screen_width * 0.6)
        cart_location = self.get_cart_location(screen_width)
        if cart_location < view_width // 2:
            slice_range = slice(view_width)
        elif cart_location > (screen_width - view_width // 2):
            slice_range = slice(-view_width, None)
        else:
            slice_range = slice(cart_location - view_width // 2, cart_location + view_width // 2)
        screen = screen[:, :, slice_range]
        screen = np.ascontiguousarray(screen, dtype=np.float32) / 255
        screen = torch.from_numpy(screen)
        return resize(screen).unsqueeze(0).to(device)

gamma = 0.999
epsilon = 0.9
steps_done = 0
num_episodes = 1000
minimal_size = 100
batch_size = 32
replay_buffer = ReplayBuffer(10000)
agent = DQN(gamma,epsilon)
return_list = []
for i in range(10):
    with tqdm(total=int(num_episodes / 10), desc='Iteration %d' % i) as pbar:
        for i_episode in range(int(num_episodes / 10)):
            done = False
            episode_return = 0
            agent.env.reset()
            last_screen = agent.get_screen()
            current_screen = agent.get_screen()
            state = current_screen - last_screen
            while not done:
                action = agent.take_action(state)
                _, reward, done, _ = agent.env.step(action.item())
                episode_return += reward
                reward = torch.tensor([reward], device=device)
                last_screen = current_screen
                current_screen = agent.get_screen()
                next_state = current_screen - last_screen

                replay_buffer.add(state, action, next_state, reward)
                state = next_state
                if replay_buffer.size() > minimal_size:
                    transition_dict = replay_buffer.sample(batch_size)
                    agent.update(transition_dict)
            return_list.append(episode_return)
            if (i_episode + 1) % 10 == 0:
                agent.target_net.load_state_dict(agent.policy_net.state_dict())
                pbar.set_postfix({
                    'episode':
                        '%d' % (num_episodes / 10 * i + i_episode + 1),
                    'return':
                        '%.3f' % np.mean(return_list[-10:])
                })
            pbar.update(1)
episodes_list = list(range(len(return_list)))
plt.plot(episodes_list, return_list)
plt.xlabel('Episodes')
plt.ylabel('Returns')
plt.title('DQN on {}'.format("CartPole-v0"))
plt.show()

mv_return = moving_average(return_list, 9)
plt.plot(episodes_list, mv_return)
plt.xlabel('Episodes')
plt.ylabel('Returns')
plt.title('DQN on {}'.format("CartPole-v0"))
plt.show()

2，Double DQN

2.1，Inverted Pendulum环境

该环境下有一个处于随机位置的倒立摆，环境的状态包括倒立摆角度的正弦值 ，余弦值 ，角速度 ；动作为对倒立摆施加的力矩。每一步都会根据当前倒立摆的状态的好坏给予智能体不同的奖励，该环境的奖励函数为 ，倒立摆向上保持直立不动时奖励为 0，倒立摆在其他位置时奖励为负数。环境本身没有终止状态，运行 200 步后游戏自动结束。

标号	名称	最小值	最大值
0		-1.0	1.0
1		-1.0	1.0
2		-8.0	8.0

标号	动作	最小值	最大值
0	力矩	-2.0	2.0

力矩大小是在  范围内的连续值。由于 DQN 只能处理离散动作环境，因此我们无法直接用 DQN 来处理倒立摆环境，但倒立摆环境可以比较方便地验证 DQN 对值的过高估计：倒立摆环境下  值的最大估计应为 0（倒立摆向上保持直立时能选取的最大  值）， 值出现大于 0 的情况则说明出现了过高估计。为了能够应用 DQN，我们采用离散化动作的技巧。例如，下面的代码将连续的动作空间离散为 11 个动作。动作 分别代表力矩为 。

2.2，Double DQN实现

import random
import gym
import numpy as np
import torch
import torch.nn.functional as F
import matplotlib.pyplot as plt
import rl_utils
from tqdm import tqdm

class Qnet(torch.nn.Module):
    ''' 只有一层隐藏层的Q网络 '''
    def __init__(self, state_dim, hidden_dim, action_dim):
        super(Qnet, self).__init__()
        self.fc1 = torch.nn.Linear(state_dim, hidden_dim)
        self.fc2 = torch.nn.Linear(hidden_dim, action_dim)

    def forward(self, x):
        x = F.relu(self.fc1(x))
        return self.fc2(x)

接下来在 DQN 代码的基础上稍做修改以实现 Double DQN。

class DQN:
    ''' DQN算法,包括Double DQN '''
    def __init__(self,state_dim,hidden_dim,action_dim,learning_rate,gamma,epsilon,target_update,device,dqn_type='VanillaDQN'):
        self.action_dim = action_dim
        self.q_net = Qnet(state_dim, hidden_dim, self.action_dim).to(device)
        self.target_q_net = Qnet(state_dim, hidden_dim,self.action_dim).to(device)
        self.optimizer = torch.optim.Adam(self.q_net.parameters(),lr=learning_rate)
        self.gamma = gamma
        self.epsilon = epsilon
        self.target_update = target_update
        self.count = 0
        self.dqn_type = dqn_type
        self.device = device

    def take_action(self, state):
        if np.random.random() < self.epsilon:
            action = np.random.randint(self.action_dim)
        else:
            state = torch.tensor([state], dtype=torch.float).to(self.device)
            action = self.q_net(state).argmax().item()
        return action

    def max_q_value(self, state):
        state = torch.tensor([state], dtype=torch.float).to(self.device)
        return self.q_net(state).max().item()

    def update(self, transition_dict):
        states = torch.tensor(transition_dict['states'],dtype=torch.float).to(self.device)
        actions = torch.tensor(transition_dict['actions']).view(-1, 1).to(self.device)
        rewards = torch.tensor(transition_dict['rewards'],dtype=torch.float).view(-1, 1).to(self.device)
        next_states = torch.tensor(transition_dict['next_states'],dtype=torch.float).to(self.device)
        dones = torch.tensor(transition_dict['dones'],dtype=torch.float).view(-1, 1).to(self.device)

        q_values = self.q_net(states).gather(1, actions)  # Q值
        # 下个状态的最大Q值
        if self.dqn_type == 'DoubleDQN':
            max_action = self.q_net(next_states).max(1)[1].view(-1, 1)
            max_next_q_values = self.target_q_net(next_states).gather(1, max_action)
        else:
            max_next_q_values = self.target_q_net(next_states).max(1)[0].view(-1, 1)
        # max_next_q_values = self.target_q_net(next_states).max(1)[0].view(-1, 1)
        q_targets = rewards + self.gamma * max_next_q_values * (1 - dones)  # TD误差目标
        dqn_loss = torch.mean(F.mse_loss(q_values, q_targets))  # 均方误差损失函数
        self.optimizer.zero_grad()  # PyTorch中默认梯度会累积,这里需要显式将梯度置为0
        dqn_loss.backward()  # 反向传播更新参数
        self.optimizer.step()

        if self.count % self.target_update == 0:
            self.target_q_net.load_state_dict(
                self.q_net.state_dict())  # 更新目标网络
        self.count += 1

接下来我们设置相应的超参数，并实现将倒立摆环境中的连续动作转化为离散动作的函数。

lr = 1e-2
num_episodes = 200
hidden_dim = 128
gamma = 0.98
epsilon = 0.01
target_update = 50
buffer_size = 5000
minimal_size = 1000
batch_size = 64
device = torch.device("cuda") if torch.cuda.is_available() else torch.device("cpu")

env_name = 'Pendulum-v1'
env = gym.make(env_name)
state_dim = env.observation_space.shape[0]
action_dim = 11  # 将连续动作分成11个离散动作

def dis_to_con(discrete_action, env, action_dim):  # 离散动作转回连续的函数
    action_lowbound = env.action_space.low[0]  # 连续动作的最小值
    action_upbound = env.action_space.high[0]  # 连续动作的最大值
    return action_lowbound + (discrete_action / (action_dim - 1)) * (action_upbound - action_lowbound)

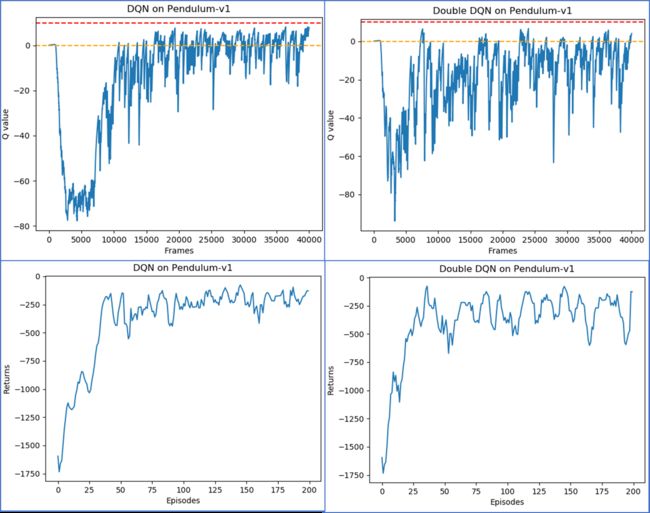
接下来要对比 DQN 和 Double DQN 的训练情况，为了便于后续多次调用，我们进一步将 DQN 算法的训练过程定义成一个函数。训练过程会记录下每个状态的最大  值，在训练完成后我们可以将结果可视化，观测这些  值存在的过高估计的情况，以此来对比 DQN 和 Double DQN 的不同。

def train_DQN(agent, env, num_episodes, replay_buffer, minimal_size,batch_size):
    return_list = []
    max_q_value_list = []
    max_q_value = 0
    for i in range(10):
        with tqdm(total=int(num_episodes / 10),
                  desc='Iteration %d' % i) as pbar:
            for i_episode in range(int(num_episodes / 10)):
                episode_return = 0
                state = env.reset()
                env.render()
                done = False
                while not done:
                    action = agent.take_action(state)
                    max_q_value = agent.max_q_value(
                        state) * 0.005 + max_q_value * 0.995  # 平滑处理
                    max_q_value_list.append(max_q_value)  # 保存每个状态的最大Q值
                    action_continuous = dis_to_con(action, env,agent.action_dim)
                    next_state, reward, done, _ = env.step([action_continuous])
                    replay_buffer.add(state, action, reward, next_state, done)
                    state = next_state
                    episode_return += reward
                    if replay_buffer.size() > minimal_size:
                        b_s, b_a, b_r, b_ns, b_d = replay_buffer.sample(
                            batch_size)
                        transition_dict = {
                            'states': b_s,
                            'actions': b_a,
                            'next_states': b_ns,
                            'rewards': b_r,
                            'dones': b_d
                        }
                        agent.update(transition_dict)
                return_list.append(episode_return)
                if (i_episode + 1) % 10 == 0:
                    pbar.set_postfix({
                        'episode':
                        '%d' % (num_episodes / 10 * i + i_episode + 1),
                        'return':
                        '%.3f' % np.mean(return_list[-10:])
                    })
                pbar.update(1)
    return return_list, max_q_value_list

random.seed(0)
np.random.seed(0)
env.seed(0)
torch.manual_seed(0)
replay_buffer = rl_utils.ReplayBuffer(buffer_size)
agent = DQN(state_dim, hidden_dim, action_dim, lr, gamma, epsilon,target_update, device)
#agent = DQN(state_dim, hidden_dim, action_dim, lr, gamma, epsilon,target_update, device, 'DoubleDQN')
return_list, max_q_value_list = train_DQN(agent, env, num_episodes,replay_buffer, minimal_size,batch_size)

episodes_list = list(range(len(return_list)))
mv_return = rl_utils.moving_average(return_list, 5)
plt.plot(episodes_list, mv_return)
plt.xlabel('Episodes')
plt.ylabel('Returns')
#plt.title('Double DQN on {}'.format(env_name))
plt.title('DQN on {}'.format(env_name))
plt.show()

frames_list = list(range(len(max_q_value_list)))
plt.plot(frames_list, max_q_value_list)
plt.axhline(0, c='orange', ls='--')
plt.axhline(10, c='red', ls='--')
plt.xlabel('Frames')
plt.ylabel('Q value')
#plt.title('Double DQN on {}'.format(env_name))
plt.title('DQN on {}'.format(env_name))
plt.show()

我们可以发现，与普通的 DQN 相比，Double DQN 比较少出现  值大于 0 的情况，说明值过高估计的问题得到了很大缓解。

3，Dueling DQN算法

3.1，算法简介

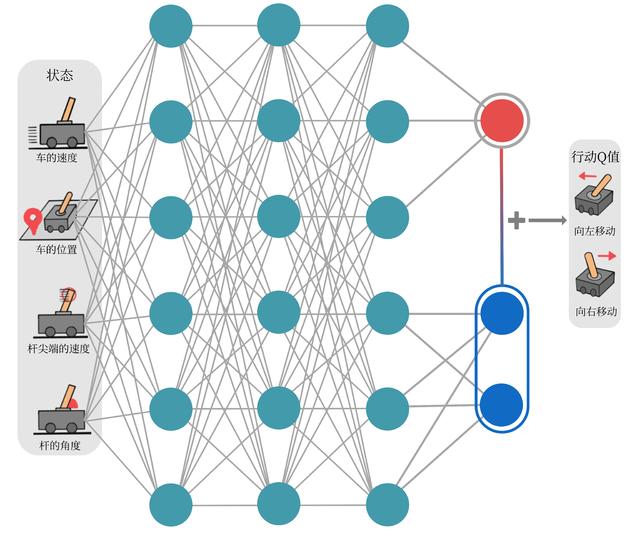
Dueling DQN 是 DQN 另一种的改进算法，它在传统 DQN 的基础上只进行了微小的改动，但却能大幅提升 DQN 的表现。在强化学习中，我们将状态动作价值函数减去状态价值函数的结果定义为优势函数 ，即 。在同一个状态下，所有动作的优势值之和为 0，因为所有动作的动作价值的期望就是这个状态的状态价值。

将状态价值函数和优势函数分别建模的好处在于：某些情境下智能体只会关注状态的价值，而并不关心不同动作导致的差异，此时将二者分开建模能够使智能体更好地处理与动作关联较小的状态。在驾驶车辆游戏中，智能体注意力集中的部位被显示为橙色，当智能体前面没有车时，车辆自身动作并没有太大差异，此时智能体更关注状态价值，而当智能体前面有车时（智能体需要超车），智能体开始关注不同动作优势值的差异。

3.2，Dueling DQN实现

Dueling DQN 与 DQN 相比的差异只是在网络结构上，大部分代码依然可以继续沿用。我们定义状态价值函数和优势函数的复合神经网络VAnet。

class VAnet(torch.nn.Module):
    ''' 只有一层隐藏层的A网络和V网络 '''
    def __init__(self, state_dim, hidden_dim, action_dim):
        super(VAnet, self).__init__()
        self.fc1 = torch.nn.Linear(state_dim, hidden_dim)  # 共享网络部分
        self.fc_A = torch.nn.Linear(hidden_dim, action_dim)
        self.fc_V = torch.nn.Linear(hidden_dim, 1)

    def forward(self, x):
        A = self.fc_A(F.relu(self.fc1(x)))
        V = self.fc_V(F.relu(self.fc1(x)))
        Q = V + A - A.mean(1).view(-1, 1)  # Q值由V值和A值计算得到
        return Q

class DQN:
    ''' DQN算法,包括Double DQN和Dueling DQN '''
    def __init__(self,
                 state_dim,
                 hidden_dim,
                 action_dim,
                 learning_rate,
                 gamma,
                 epsilon,
                 target_update,
                 device,
                 dqn_type='VanillaDQN'):
        self.action_dim = action_dim
        if dqn_type == 'DuelingDQN':  # Dueling DQN采取不一样的网络框架
            self.q_net = VAnet(state_dim, hidden_dim,
                               self.action_dim).to(device)
            self.target_q_net = VAnet(state_dim, hidden_dim,
                                      self.action_dim).to(device)
        else:
            self.q_net = Qnet(state_dim, hidden_dim,
                              self.action_dim).to(device)
            self.target_q_net = Qnet(state_dim, hidden_dim,
                                     self.action_dim).to(device)
        self.optimizer = torch.optim.Adam(self.q_net.parameters(),
                                          lr=learning_rate)
        self.gamma = gamma
        self.epsilon = epsilon
        self.target_update = target_update
        self.count = 0
        self.dqn_type = dqn_type
        self.device = device

    def take_action(self, state):
        if np.random.random() < self.epsilon:
            action = np.random.randint(self.action_dim)
        else:
            state = torch.tensor([state], dtype=torch.float).to(self.device)
            action = self.q_net(state).argmax().item()
        return action

    def max_q_value(self, state):
        state = torch.tensor([state], dtype=torch.float).to(self.device)
        return self.q_net(state).max().item()

    def update(self, transition_dict):
        states = torch.tensor(transition_dict['states'],
                              dtype=torch.float).to(self.device)
        actions = torch.tensor(transition_dict['actions']).view(-1, 1).to(
            self.device)
        rewards = torch.tensor(transition_dict['rewards'],
                               dtype=torch.float).view(-1, 1).to(self.device)
        next_states = torch.tensor(transition_dict['next_states'],
                                   dtype=torch.float).to(self.device)
        dones = torch.tensor(transition_dict['dones'],
                             dtype=torch.float).view(-1, 1).to(self.device)

        q_values = self.q_net(states).gather(1, actions)
        if self.dqn_type == 'DoubleDQN':
            max_action = self.q_net(next_states).max(1)[1].view(-1, 1)
            max_next_q_values = self.target_q_net(next_states).gather(
                1, max_action)
        else:
            max_next_q_values = self.target_q_net(next_states).max(1)[0].view(
                -1, 1)
        q_targets = rewards + self.gamma * max_next_q_values * (1 - dones)
        dqn_loss = torch.mean(F.mse_loss(q_values, q_targets))
        self.optimizer.zero_grad()
        dqn_loss.backward()
        self.optimizer.step()

        if self.count % self.target_update == 0:
            self.target_q_net.load_state_dict(self.q_net.state_dict())
        self.count += 1

random.seed(0)
np.random.seed(0)
env.seed(0)
torch.manual_seed(0)
replay_buffer = rl_utils.ReplayBuffer(buffer_size)
agent = DQN(state_dim, hidden_dim, action_dim, lr, gamma, epsilon,
            target_update, device, 'DuelingDQN')
return_list, max_q_value_list = train_DQN(agent, env, num_episodes,replay_buffer, minimal_size,batch_size)

episodes_list = list(range(len(return_list)))
mv_return = rl_utils.moving_average(return_list, 5)
plt.plot(episodes_list, mv_return)
plt.xlabel('Episodes')
plt.ylabel('Returns')
plt.title('Dueling DQN on {}'.format(env_name))
plt.show()

frames_list = list(range(len(max_q_value_list)))
plt.plot(frames_list, max_q_value_list)
plt.axhline(0, c='orange', ls='--')
plt.axhline(10, c='red', ls='--')
plt.xlabel('Frames')
plt.ylabel('Q value')
plt.title('Dueling DQN on {}'.format(env_name))
plt.show()

根据代码运行结果我们可以发现，相比于传统的 DQN，Dueling DQN 在多个动作选择下的学习更加稳定，得到的回报最大值也更大。由 Dueling DQN 的原理可知，随着动作空间的增大，Dueling DQN 相比于 DQN 的优势更为明显。之前我们在环境中设置的离散动作数为 11，我们可以增加离散动作数（例如 15、25 等），继续进行对比实验。

4，通用格子世界

import math
import gym
from gym import spaces
from gym.utils import seeding
import numpy as np


class Grid(object):
    def __init__(self, x: int = None,y: int = None,type: int = 0,reward: int = 0.0,value: float = 0.0):  # value, for possible future usage
        self.x = x  # coordinate x
        self.y = y
        self.type = value  # Type (0:empty；1:obstacle or boundary)
        self.reward = reward  # instant reward for an agent entering this grid cell
        self.value = value  # the value of this grid cell, for future usage
        self.name = None  # name of this grid.
        self._update_name()

    def _update_name(self):
        self.name = "X{0}-Y{1}".format(self.x, self.y)

    def __str__(self):
        return "name:{4}, x:{0}, y:{1}, type:{2}, value{3}".format(self.x,self.y,self.type,self.reward,self.value,self.name)

class GridMatrix(object):
    '''格子矩阵，通过不同的设置，模拟不同的格子世界环境
    '''
    def __init__(self, n_width: int,  # defines the number of cells horizontally
                 n_height: int,  # vertically
                 default_type: int = 0,  # default cell type
                 default_reward: float = 0.0,  # default instant reward
                 default_value: float = 0.0  # default value
                 ):
        self.grids = None
        self.n_height = n_height
        self.n_width = n_width
        self.len = n_width * n_height
        self.default_reward = default_reward
        self.default_value = default_value
        self.default_type = default_type
        self.reset()

    def reset(self):
        self.grids = []
        for x in range(self.n_height):
            for y in range(self.n_width):
                self.grids.append(Grid(x,y,self.default_type,self.default_reward,self.default_value))

    def get_grid(self, x, y=None):
        '''get a grid information
        args: represented by x,y or just a tuple type of x
        return: grid object
        '''
        xx, yy = None, None
        if isinstance(x, int):
            xx, yy = x, y
        elif isinstance(x, tuple):
            xx, yy = x[0], x[1]
        assert (xx >= 0 and yy >= 0 and xx < self.n_width and yy < self.n_height), \
            "coordinates should be in reasonable range"
        index = yy * self.n_width + xx
        return self.grids[index]

    def set_reward(self, x, y, reward):
        grid = self.get_grid(x, y)
        if grid is not None:
            grid.reward = reward
        else:
            raise ("grid doesn't exist")

    def set_value(self, x, y, value):
        grid = self.get_grid(x, y)
        if grid is not None:
            grid.value = value
        else:
            raise ("grid doesn't exist")

    def set_type(self, x, y, type):
        grid = self.get_grid(x, y)
        if grid is not None:
            grid.type = type
        else:
            raise ("grid doesn't exist")

    def get_reward(self, x, y):
        grid = self.get_grid(x, y)
        if grid is None:
            return None
        return grid.reward

    def get_value(self, x, y):
        grid = self.get_grid(x, y)
        if grid is None:
            return None
        return grid.value

    def get_type(self, x, y):
        grid = self.get_grid(x, y)
        if grid is None:
            return None
        return grid.type


class GridWorldEnv(gym.Env):
    '''格子世界环境，可以模拟各种不同的格子世界
    '''
    metadata = {
        'render.modes': ['human', 'rgb_array'],
        'video.frames_per_second': 30
    }
    def __init__(self, n_width: int = 10,n_height: int = 7,u_size=40,default_reward: float = 0,default_type=0,windy=False,state=0):
        self.u_size = u_size  # size for each cell (pixels)
        self.n_width = n_width  # width of the env calculated by number of cells.
        self.n_height = n_height  # height...
        self.width = u_size * n_width  # scenario width (pixels)
        self.height = u_size * n_height  # height
        self.default_reward = default_reward
        self.default_type = default_type
        self.state = state
        self._adjust_size()

        self.grids = GridMatrix(n_width=self.n_width,n_height=self.n_height,default_reward=self.default_reward,default_type=self.default_type,default_value=0.0)
        self.reward = 0  # for rendering
        self.action = None  # for rendering
        self.windy = windy  # whether this is a windy environment

        # 0,1,2,3,4 represent left, right, up, down, -, five moves.
        self.action_space = spaces.Discrete(4)
        # 观察空间由low和high决定
        self.observation_space = spaces.Discrete(self.n_height * self.n_width)
        # 坐标原点为左下角，这个pyglet是一致的, left-bottom corner is the position of (0,0)
        # 通过设置起始点、终止点以及特殊奖励和类型的格子可以构建各种不同类型的格子世界环境
        # 比如：随机行走、汽车租赁、悬崖行走等David Silver公开课中的示例
        self.ends = [(7, 3)]  # 终止格子坐标，可以有多个, goal cells position list
        self.start = (0, 3)  # 起始格子坐标，只有一个, start cell position, only one start position
        self.types = []  # 特殊种类的格子在此设置。[(3,2,1)]表示(3,2)处值为1.
        # special type of cells, (x,y,z) represents in position(x,y) the cell type is z
        self.rewards = []  # 特殊奖励的格子在此设置，终止格子奖励0, special reward for a cell
        self.refresh_setting()
        self.viewer = None  # 图形接口对象
        self._seed()  # 产生一个随机子
        self._reset()

    def _adjust_size(self):
        '''调整场景尺寸适合最大宽度、高度不超过800
        '''
        pass

    def _seed(self, seed=None):
        # 产生一个随机化时需要的种子，同时返回一个np_random对象，支持后续的随机化生成操作
        self.np_random, seed = seeding.np_random(seed)
        return [seed]

    def _step(self, action):
        assert self.action_space.contains(action), \
            "%r (%s) invalid" % (action, type(action))

        self.action = action  # action for rendering
        old_x, old_y = self._state_to_xy(self.state)
        new_x, new_y = old_x, old_y

        # wind effect:
        # 有风效果，其数字表示个体离开(而不是进入)该格子时朝向别的方向会被吹偏离的格子数
        # this effect is just used for the windy env in David Silver's youtube video.
        if self.windy:
            if new_x in [3, 4, 5, 8]:
                new_y += 1
            elif new_x in [6, 7]:
                new_y += 2

        if action == 0:
            new_x -= 1  # left
        elif action == 1:
            new_x += 1  # right
        elif action == 2:
            new_y += 1  # up
        elif action == 3:
            new_y -= 1  # down

        elif action == 4:
            new_x, new_y = new_x - 1, new_y - 1
        elif action == 5:
            new_x, new_y = new_x + 1, new_y - 1
        elif action == 6:
            new_x, new_y = new_x + 1, new_y - 1
        elif action == 7:
            new_x, new_y = new_x + 1, new_y + 1
        # boundary effect
        if new_x < 0: new_x = 0
        if new_x >= self.n_width: new_x = self.n_width - 1
        if new_y < 0: new_y = 0
        if new_y >= self.n_height: new_y = self.n_height - 1

        # wall effect, obstacles or boundary.
        # 类型为1的格子为障碍格子，不可进入
        if self.grids.get_type(new_x, new_y) == 1:
            new_x, new_y = old_x, old_y

        self.reward = self.grids.get_reward(new_x, new_y)

        done = self._is_end_state(new_x, new_y)
        self.state = self._xy_to_state(new_x, new_y)
        # 提供格子世界所有的信息在info内
        info = {"x": new_x, "y": new_y, "grids": self.grids}
        return self.state, self.reward, done, info

    # 将状态变为横纵坐标, set status into an one-axis coordinate value
    def _state_to_xy(self, s):
        x = s % self.n_width
        y = int((s - x) / self.n_width)
        return x, y

    def _xy_to_state(self, x, y=None):
        if isinstance(x, int):
            assert (isinstance(y, int)), "incomplete Position info"
            return x + self.n_width * y
        elif isinstance(x, tuple):
            return x[0] + self.n_width * x[1]
        return -1  # 未知状态, unknow status

    def refresh_setting(self):
        '''用户在使用该类创建格子世界后可能会修改格子世界某些格子类型或奖励值
        的设置，修改设置后通过调用该方法使得设置生效。
        '''
        for x, y, r in self.rewards:
            self.grids.set_reward(x, y, r)
        for x, y, t in self.types:
            self.grids.set_type(x, y, t)

    def _reset(self):
        self.state = self._xy_to_state(self.start)
        return self.state

        # 判断是否是终止状态

    def _is_end_state(self, x, y=None):
        if y is not None:
            xx, yy = x, y
        elif isinstance(x, int):
            xx, yy = self._state_to_xy(x)
        else:
            assert (isinstance(x, tuple)), "incomplete coordinate values"
            xx, yy = x[0], x[1]
        for end in self.ends:
            if xx == end[0] and yy == end[1]:
                return True
        return False

    # 图形化界面, Graphic UI
    def render(self, mode='human', close=False):
        if close:
            if self.viewer is not None:
                self.viewer.close()
                self.viewer = None
            return
        zero = (0, 0)
        u_size = self.u_size
        m = 2  # gaps between two cells

        # 如果还没有设定屏幕对象，则初始化整个屏幕具备的元素。
        if self.viewer is None:
            from gym.envs.classic_control import rendering
            self.viewer = rendering.Viewer(self.width, self.height)

            # 在Viewer里绘制一个几何图像的步骤如下：
            # the following steps just tells how to render an shape in the environment.
            # 1. 建立该对象需要的数据本身
            # 2. 使用rendering提供的方法返回一个geom对象
            # 3. 对geom对象进行一些对象颜色、线宽、线型、变换属性的设置（有些对象提供一些个
            #    性化的方法来设置属性，具体请参考继承自这些Geom的对象），这其中有一个重要的
            #    属性就是变换属性，
            #    该属性负责对对象在屏幕中的位置、渲染、缩放进行渲染。如果某对象
            #    在呈现时可能发生上述变化，则应建立关于该对象的变换属性。该属性是一个
            #    Transform对象，而一个Transform对象，包括translate、rotate和scale
            #    三个属性，每个属性都由以np.array对象描述的矩阵决定。
            # 4. 将新建立的geom对象添加至viewer的绘制对象列表里，如果在屏幕上只出现一次，
            #    将其加入到add_onegeom(）列表中，如果需要多次渲染，则将其加入add_geom()
            # 5. 在渲染整个viewer之前，对有需要的geom的参数进行修改，修改主要基于该对象
            #    的Transform对象
            # 6. 调用Viewer的render()方法进行绘制
            ''' 绘制水平竖直格子线，由于设置了格子之间的间隙，可不用此段代码
            for i in range(self.n_width+1):
                line = rendering.Line(start = (i*u_size, 0), 
                                      end =(i*u_size, u_size*self.n_height))
                line.set_color(0.5,0,0)
                self.viewer.add_geom(line)
            for i in range(self.n_height):
                line = rendering.Line(start = (0, i*u_size),
                                      end = (u_size*self.n_width, i*u_size))
                line.set_color(0,0,1)
                self.viewer.add_geom(line)
            '''

            # 绘制格子, draw cells
            for x in range(self.n_width):
                for y in range(self.n_height):
                    v = [(x * u_size + m, y * u_size + m),
                         ((x + 1) * u_size - m, y * u_size + m),
                         ((x + 1) * u_size - m, (y + 1) * u_size - m),
                         (x * u_size + m, (y + 1) * u_size - m)]

                    rect = rendering.FilledPolygon(v)
                    r = self.grids.get_reward(x, y) / 10
                    if r < 0:
                        rect.set_color(0.9 - r, 0.9 + r, 0.9 + r)
                    elif r > 0:
                        rect.set_color(0.3, 0.5 + r, 0.3)
                    else:
                        rect.set_color(0.9, 0.9, 0.9)
                    self.viewer.add_geom(rect)
                    # 绘制边框, draw frameworks
                    v_outline = [(x * u_size + m, y * u_size + m),
                                 ((x + 1) * u_size - m, y * u_size + m),
                                 ((x + 1) * u_size - m, (y + 1) * u_size - m),
                                 (x * u_size + m, (y + 1) * u_size - m)]
                    outline = rendering.make_polygon(v_outline, False)
                    outline.set_linewidth(3)

                    if self._is_end_state(x, y):
                        # 给终点方格添加金黄色边框, give end state cell a yellow outline.
                        outline.set_color(0.9, 0.9, 0)
                        self.viewer.add_geom(outline)
                    if self.start[0] == x and self.start[1] == y:
                        outline.set_color(0.5, 0.5, 0.8)
                        self.viewer.add_geom(outline)
                    if self.grids.get_type(x, y) == 1:  # 障碍格子用深灰色表示, obstacle cells are with gray color
                        rect.set_color(0.3, 0.3, 0.3)
                    else:
                        pass
            # 绘制个体, draw agent
            self.agent = rendering.make_circle(u_size / 4, 30, True)
            self.agent.set_color(1.0, 1.0, 0.0)
            self.viewer.add_geom(self.agent)
            self.agent_trans = rendering.Transform()
            self.agent.add_attr(self.agent_trans)

        # 更新个体位置 update position of an agent
        x, y = self._state_to_xy(self.state)
        self.agent_trans.set_translation((x + 0.5) * u_size, (y + 0.5) * u_size)

        return self.viewer.render(return_rgb_array=mode == 'rgb_array')

def LargeGridWorld():
    '''10*10的一个格子世界环境，设置参照：
    http://cs.stanford.edu/people/karpathy/reinforcejs/gridworld_td.html
    '''
    env = GridWorldEnv(n_width=10,n_height=10,u_size=40,default_reward=0,default_type=0,windy=False)
    env.start = (0, 9)
    env.ends = [(5, 4)]
    env.types = [(4, 2, 1), (4, 3, 1), (4, 4, 1), (4, 5, 1), (4, 6, 1), (4, 7, 1),
                 (1, 7, 1), (2, 7, 1), (3, 7, 1), (4, 7, 1), (6, 7, 1), (7, 7, 1),
                 (8, 7, 1)]
    env.rewards = [(3, 2, -1), (3, 6, -1), (5, 2, -1), (6, 2, -1), (8, 3, -1),
                   (8, 4, -1), (5, 4, 1), (6, 4, -1), (5, 5, -1), (6, 5, -1)]
    env.refresh_setting()
    return env

def SimpleGridWorld():
    '''无风10*7的格子，设置参照： David Silver强化学习公开课视频 第3讲
    '''
    env = GridWorldEnv(n_width=10, n_height=7,u_size=60,default_reward=-1,default_type=0,windy=False)
    env.start = (0, 3)
    env.ends = [(7, 3)]
    env.rewards = [(7, 3, 1)]
    env.refresh_setting()
    return env

def WindyGridWorld():
    '''有风10*7的格子，设置参照： David Silver强化学习公开课视频 第5讲
    '''
    env = GridWorldEnv(n_width=10,n_height=7,u_size=60,default_reward=-1,default_type=0,windy=True)
    env.start = (0, 3)
    env.ends = [(7, 3)]
    env.rewards = [(7, 3, 1)]

    env.refresh_setting()
    return env

def RandomWalk():
    '''随机行走示例环境
    '''
    env = GridWorldEnv(n_width=7,
                       n_height=1,
                       u_size=80,
                       default_reward=0,
                       default_type=0,
                       windy=False)
    env.action_space = spaces.Discrete(2)  # left or right
    env.start = (3, 0)
    env.ends = [(6, 0), (0, 0)]
    env.rewards = [(6, 0, 1)]
    env.refresh_setting()
    return env

def CliffWalk():
    '''悬崖行走格子世界环境
    '''
    env = GridWorldEnv(n_width=12,
                       n_height=4,
                       u_size=60,
                       default_reward=-1,
                       default_type=0,
                       windy=False)
    env.action_space = spaces.Discrete(4)  # left or right
    env.start = (0, 0)
    env.ends = [(11, 0)]
    # env.rewards=[]
    # env.types = [(5,1,1),(5,2,1)]
    for i in range(10):
        env.rewards.append((i + 1, 0, -100))
        env.ends.append((i + 1, 0))
    env.refresh_setting()
    return env

def SkullAndTreasure():
    '''骷髅与钱币示例，解释随机策略的有效性 David Silver 强化学习公开课第六讲 策略梯度
    Examples of Skull and Money explained the necessity and effectiveness
    '''
    env = GridWorldEnv(n_width=5,n_height=2,u_size=60,default_reward=-1,default_type=0,windy=False)
    env.action_space = spaces.Discrete(4)  # left or right
    env.start = (0, 1)
    env.ends = [(2, 0)]
    env.rewards = [(0, 0, -100), (2, 0, 100), (4, 0, -100)]
    env.types = [(1, 0, 1), (3, 0, 1)]
    env.refresh_setting()
    return env


if __name__ == "__main__":
    env = SkullAndTreasure()
    print("hello")
    env._reset()
    nfs = env.observation_space
    nfa = env.action_space
    print("nfs:%s; nfa:%s" % (nfs, nfa))
    print(env.observation_space)
    print(env.action_space)
    print(env.state)
    env._reset()
    env.render()
    # x = input("press any key to exit")
    for _ in range(20000):
        env.render()
        a = env.action_space.sample()
        state, reward, isdone, info = env._step(a)
        print("{0}, {1}, {2}, {3}".format(a, reward, isdone, info))

    print("env closed")