吴恩达深度学习系列课程随记——Course4Week1
1.计算机视觉
任务:
图片分类/识别:图片是不是猫
目标检测:图片中所有车的位置
图片风格迁移:让一张图看起来像毕加索画的
挑战:
数据可能很大,如1k*1k的图片有300万维输入,如果有1000个隐藏单元,一层W会有30亿个参数
因此,需要卷积
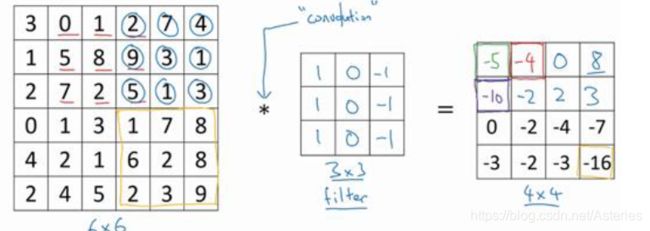
2.边缘检测示例
滑动窗口对位相乘,称为卷积运算,小的那个矩阵称为核或者过滤器
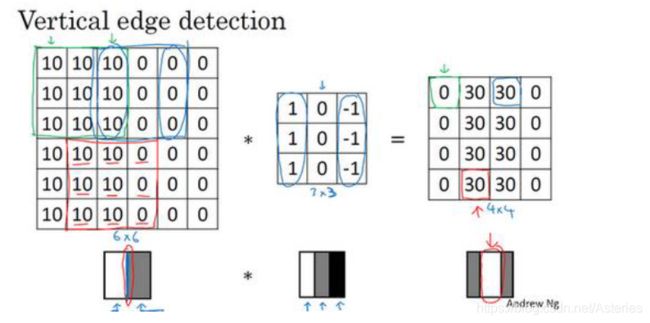
图中这个过滤器,用来检测垂直边缘。将它反转一下,可以检测水平边缘。(这是从结果看出的,中间的30就是边缘)
3.更多边缘检测内容
观察上一节卷积运算的结果,我们可以总结过滤器就像是一种特征图像的简化,负数是暗,正数是亮,0是边缘。
对于上一节的垂直过滤器,结果中表示边缘的部分是正的,这表示亮到暗过渡(因为过滤器左1右0)
如果是-30,那显然就是暗到亮过渡。翻转一下,同理,用来检测水平边缘。如果一个滑动窗口包含的部分有两个方向的过渡,结果中会表现为一个绝对值较小的数,因为一部分相抵了。
我们发现不同的过滤器可以达到不同的运算效果,检测不同类型的边缘。
Sobel过滤器,增加了中间元素权重,使得算法稳定性更好:
Sharr过滤器:
可以把过滤器的9个数字当成9个参数,来进行你的深度学习
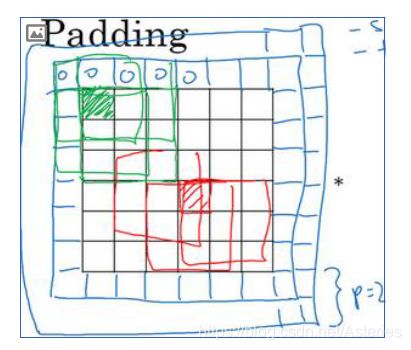
4.Padding(填充)
图像维度是n*n,过滤器是f*f,显然得到结果的维度应该是:
![]()
这称为Valid卷积
这样有两个缺点:
一来卷积操作缩小了图像
二来图像角落的像素在计算中涉及太少,有信息丢失
我们可以填充,将图像向各个方向拓展p个单位像素的长度,输出维度变为:
![]()
如果使得输出的尺寸等于原尺寸,这称为Same卷积。这时容易求得:
应用中f很少取偶数,因为:
取偶数后Same卷积中p取不到整数,只能进行一些非对称的填充
奇数f的过滤器有中心点,这便于指出过滤器的位置
5.卷积步长
步长:
卷积算法中,窗口滑动一次移动多少个元素,设为s
输出的维度现在变化为:
这意味着如果滑动窗口有一部分在图像外面,我们直接放弃相乘操作。
一个细节:
数学上的卷积常常要先把过滤器处理一下得到镜像:先顺时针翻转90度,再上下取镜像。而我们的操作被称为互相关。
但机器学习领域里就把它叫卷积。
6.三维卷积
使用一个三维过滤器,其第三维和图像的第三维大小相同,然后按照二维的方法滑动,得到一个二维结果。
过滤器的设置:
需要检测第几层的边缘,就设置那一层对应位置的过滤器为之前的二维过滤器的数值,其他层的全部设为0
如果不在乎边缘在哪一层,直接设一个各层相同的过滤器。
理论上图像识别中,有红绿蓝三层,只关注其中一层是可行的。
怎么同时使用多个过滤器,比如同时检测水平和垂直边缘,或是倾斜边缘:
将几个过滤器的结果叠起来形成三维的输出。
维度细节:
输入:
![]()
过滤器:
![]()
输出(最后一项是过滤器个数):
![]()
这里没有考虑填充,nc称为通道数,也叫三维立方体的深度。
7.单层卷积网络
此时的W其实就表示进行卷积操作,我们会得到此前叙述过的维度的结果。
而b也与之前类似,是一个偏差量,这里对于每一个过滤器,b是不同的。
记号总结,其中f,l,p等的含义与此前讲的相同:
过滤器维度:
![]()
W的维度:
![]()
A的维度:
![]()
8.简单卷积网络示例
就是此前知识的具体例子。
补充:
随着神经网络计算深度不断加深,通常开始时的图像也要更大一些
其高度和宽度会在一段时间内保持一致,然后随着网络深度的加深而逐渐减小,而通道数量在增加,
卷积层常常用CONV来标注,常见层还有池化层,我们称之为POOL(之后讲)。
最后一个是全连接层,用FC 表示。
虽然仅用卷积层也有可能构建出很好的神经网络,但大部分神经望楼架构师依然会添加池化层和全连接层。
9.池化层
卷积网络也经常使用池化层来缩减模型的大小,提高计算速度,同时提高所提取特征的鲁棒性。
池化层与卷积层类似,只是过滤器的作用变成了池化,如果输入多个通道,就让过滤器对每个通道分别池化。
常用的一种池化是最大池化:
过滤器的作用为取范围内的最大值
也有平均池化,过滤器的作用是去范围内的平均值,不常用。
注意池化过程中没有需要学习的参数,执行反向传播时,反向传播没有参数适用于最大池化。
10.卷积神经网络示例
我用的这个网络模型和经典网络 LeNet-5 非常相似。模式是一个卷积和一个池化层作为一组一同出现。
人们在计算神经网络有多少层时,通常只统计具有权重和参数的层。
因为池化层没有权重和参数,只有一些超参数。这里,我们把CONV1和 POOL1 共同作为一个卷积,并标记为 Layer1。
我们注意到上节课提过的:
随着神经网络深度的加深,高度和宽度通常都会减少,而通道数量会增加
另一种常见模式:
一个或者多个卷几层后面一个池化层,然后一个或者多个卷积层后面再跟一个池化层,然后是几个全连接层,最后是一个 softmax
注意:
第一,池化层和最大池化层没有参数
第二,卷积层的参数相对较少,前面课上我们提到过,其实许多参数都存在于神经网络的全连接层。
观察可发现,随着神经网络的加深,激活值尺寸会逐渐变小,如果激活值尺寸下降太快,也会影响神经网络性能。
11.为什么使用卷积?
卷积层的两个主要优势在于参数共享和稀疏连接。
卷积网络映射参数远远少于普通网络,有两个原因:
一是参数共享:
观察发现,特征检测如垂直边缘检测如果适用于图片的某个区域,那么它也可能适用于图片的其他区域
不同区域中可以使用同样的参数,这种共享即使在提取高阶特征时也适用。
二是稀疏连接:
即某一输出分量只依赖于输入的一小部分而不是全部输入
卷积神经网络善于捕捉平移不变,即使输入平移几个像素结果也相似。
因为神经网络的卷积结构使得即使移动几个像素,这张图片依然具有非常相似的特征,应该属于同样的输出标记。

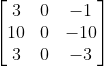
![n_{H}^{[l]}=\left \lfloor \frac{n_{H}^{[l-1]}+2p^{[l]}-f^{[l]}}{s^{[l]}}+1 \right \rfloor](http://img.e-com-net.com/image/info8/27b12db20f53427da2b257074bd07f22.gif)
![n_{W}^{[l]}=\left \lfloor \frac{n_{W}^{[l-1]}+2p^{[l]}-f^{[l]}}{s^{[l]}}+1 \right \rfloor](http://img.e-com-net.com/image/info8/fa9d076d61d741aca9eaf9238e24a3ba.gif)