什么是强化学习?(贝尔曼方程)
文章目录
-
- 什么是强化学习?(贝尔曼方程)
-
- 3.贝尔曼方程(Bellman equation)
-
- 3.1贝尔曼期望方程(Bellman expectation equation)
- 3.2 贝尔曼最优方程(Bellman optimality equation)
- 4. M D P MDP MDP 的动态编程(dynamic programming)
-
- 4.1 M D P MDP MDP
- 4.2.动态规划的局限性以及为什么需要强化学习
什么是强化学习?(贝尔曼方程)
3.贝尔曼方程(Bellman equation)
贝尔曼方程表示上述状态价值函数与状态-行为价值函数之间的关系。贝尔曼方程有贝尔曼期望方程和贝尔曼最佳方程。
3.1贝尔曼期望方程(Bellman expectation equation)
贝明期望方程可将状态价值函数和状态-行为价值函数表示为期望值 E E E。状态价值函数的贝尔曼期望方程表示如下:
V π ( s ) = E [ R t + 1 + γ V π ( S t + 1 ) ∣ S t = s ] V_{\pi}(s)=\mathbb{E}\left[R_{t+1}+\gamma V_{\pi}\left(S_{t+1}\right) \mid S_{t}=s\right] Vπ(s)=E[Rt+1+γVπ(St+1)∣St=s]当前状态 S t S_t St 的价值减价到下一状态 S t + 1 S_{t+1} St+1的价值 γ \gamma γ 乘以的期望值。
状态-行为价值函数的贝尔曼期望方程如下:
Q π ( s , a ) = E [ R t + 1 + γ Q π ( S t + 1 , A t + 1 ) ∣ S t = s , A t = a ] Q_{\pi}(s, a)=\mathbb{E}\left[R_{t+1}+\gamma Q_{\pi}\left(S_{t+1}, A_{t+1}\right) \mid S_{t}=s, A_{t}=a\right] Qπ(s,a)=E[Rt+1+γQπ(St+1,At+1)∣St=s,At=a]在当前状态 S t S_t St上执行动作 A t A_t At,这意味着期望补偿 R t + 1 R_{t+1} Rt+1加上下一个状态 S t + 1 S_{t+1} St+1 和动作 A t + 1 A_{t+1} At+1的状态-动作价值乘以折扣率。
在状态价值函数中,可以将此期望值转换为遵循策略 π π π 的状态-行为价值函数,如下所示: V π ( s ) = ∑ a ∈ A π ( a ∣ s ) Q π ( s , a ) V_{\pi}(s)=\sum_{a \in A} \pi(a \mid s) Q_{\pi}(s, a) Vπ(s)=a∈A∑π(a∣s)Qπ(s,a)状态 s s s 根据策略 π π π 选择行为 a a a 的概率乘以状态 s s s 根据 π π π 执行行为 a a a 的价值。在此公式中,状态-行为价值函数也可以用状态价值函数重新求解。
Q π ( s , a ) = R s a + γ ∑ s ′ ∈ S P s , s ′ a V π ( s ′ ) Q_{\pi}(s, a)=R_{s}^{a}+\gamma \sum_{s^{\prime} \in S} P_{s, s^{\prime}}^{a} V_{\pi}\left(s^{\prime}\right) Qπ(s,a)=Rsa+γs′∈S∑Ps,s′aVπ(s′)在当前状态 s s s 中执行行为 a a a 时,期望补偿和对下一状态 s s s 的期望值乘以状态转移概率,并加上加上折扣。
将此公式代入上面的状态值函数:
V π ( s ) = ∑ a ∈ A π ( a ∣ s ) ( R s a + γ ∑ s ′ ∈ S P s , s ′ a V π ( s ′ ) ) V_{\pi}(s)=\sum_{a \in A} \pi(a \mid s)\left(R_{s}^{a}+\gamma \sum_{s^{\prime} \in S} P_{s, s^{\prime}}^{a} V_{\pi}\left(s^{\prime}\right)\right) Vπ(s)=a∈A∑π(a∣s)(Rsa+γs′∈S∑Ps,s′aVπ(s′))这样,在价值函数表达式中,模糊期望值表达式 E E E 被减去并递归地表示。
类似地,状态-行为价值函数也可以递归地表示:
Q π ( s , a ) = R s a + γ ∑ s ′ ∈ S P s , s ′ a ∑ a ′ ∈ A π ( a ′ ∣ s ′ ) Q π ( s ′ , a ′ ) Q_{\pi}(s, a)=R_{s}^{a}+\gamma \sum_{s^{\prime} \in S} P_{s, s^{\prime}}^{a} \sum_{a^{\prime} \in A} \pi\left(a^{\prime} \mid s^{\prime}\right) Q_{\pi}\left(s^{\prime}, a^{\prime}\right) Qπ(s,a)=Rsa+γs′∈S∑Ps,s′aa′∈A∑π(a′∣s′)Qπ(s′,a′)
我们通过贝尔曼方程对状态价值函数和状态-行为价值函数进行了递归求解。
3.2 贝尔曼最优方程(Bellman optimality equation)
最佳状态价值和最佳状态-行动价值可以表述为:最佳价值是指在遵循可获得最大总回报的政策时所获得的价值。
V ∗ ( s ) = max π V π ( s ) Q ∗ ( s , a ) = max π Q π ( s , a ) \begin{aligned} V_{*}(s) &=\max _{\pi} V_{\pi}(s) \\ Q_{*}(s, a) &=\max _{\pi} Q_{\pi}(s, a) \end{aligned} V∗(s)Q∗(s,a)=πmaxVπ(s)=πmaxQπ(s,a)在 V V V 和 Q Q Q 上加上星星(*)表示最佳价值。
用贝尔曼最佳方程表示最佳价值和最佳行动价值:
V ∗ ( s ) = max a R s a + γ ∑ s ′ ∈ S P s , s ′ a V ∗ ( s ′ ) Q ∗ ( s , a ) = R s a + γ ∑ s ′ ∈ S P s , s ′ a V ∗ ( s ′ ) \begin{gathered} V_{*}(s)=\max _{a} R_{s}^{a}+\gamma \sum_{s^{\prime} \in S} P_{s, s^{\prime}}^{a} V_{*}\left(s^{\prime}\right) \\ Q_{*}(s, a)=R_{s}^{a}+\gamma \sum_{s^{\prime} \in S} P_{s, s^{\prime}}^{a} V_{*}\left(s^{\prime}\right) \end{gathered} V∗(s)=amaxRsa+γs′∈S∑Ps,s′aV∗(s′)Q∗(s,a)=Rsa+γs′∈S∑Ps,s′aV∗(s′)
4. M D P MDP MDP 的动态编程(dynamic programming)
4.1 M D P MDP MDP
让我们看一下使用达伦贝尔曼方程求解 M D P MDP MDP 的动态编程。动态编程(Dynamic Programming,DP)是一种解决递归优化问题的方法,DP由策略迭代和价值迭代组成。
重复策略(policy iteration)
重复策略将重复刷新状态价值函数,如下所示:
V k + 1 ( s ) = ∑ a ∈ A π ( a ∣ s ) ( R s a + γ ∑ s ′ ∈ S P s , s ′ a V k ( s ′ ) ) V_{k+1}(s)=\sum_{a \in A} \pi(a \mid s)\left(R_{s}^{a}+\gamma \sum_{s^{\prime} \in S} P_{s, s^{\prime}}^{a} V_{k}\left(s^{\prime}\right)\right) Vk+1(s)=a∈A∑π(a∣s)(Rsa+γs′∈S∑Ps,s′aVk(s′))
其中 k k k 表示重复过程。重复 N N N 次更新价值函数V以创建 V 1 、 V 2 、 … 和 V N V_1、V_2、…和V_N V1、V2、…和VN。这与贝尔曼期望方程的形式相同。
我们将重新导入上面的 M D P MDP MDP 示例。以下是3x3网格区域中的策略
 最初,我们允许在所有状态下以相同的0.25概率执行所有操作。未应用折扣。即,即 γ \gamma γ=1。
最初,我们允许在所有状态下以相同的0.25概率执行所有操作。未应用折扣。即,即 γ \gamma γ=1。
到达陷阱时-0.1,到达目的地时奖励1。现在,让我们看一下重复刷新状态价值函数会发生什么。
下面显示了状态价值函数在策略重复过程中的变化
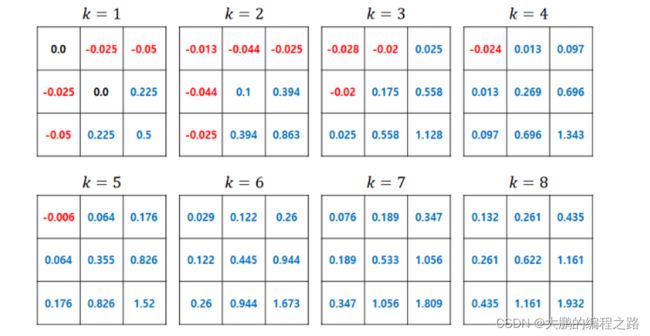
策略迭代中的状态值函数变化。当 k=8 时,策略可以更新为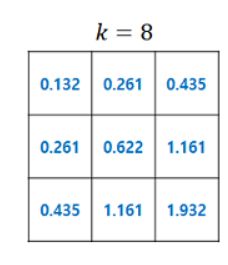
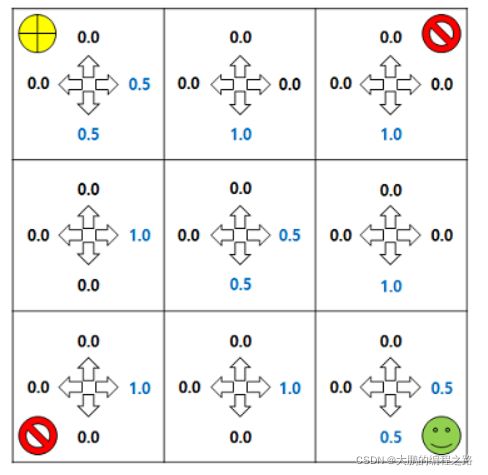
基于状态价值函数的策略更新
如果下一个状态具有与基于状态价值函数的策略更新相同的价值,则可以赋予相同的概率,使其移动到具有最高价值的状态。价值重复(value iteration)价值重复类似于策略重复。区别在于,我们首先来看一下价值重复的公式
V k + 1 ( s ) = max a ∈ A R s a + γ ∑ s ′ ∈ S P s , s ′ a V k ( s ′ ) V_{k+1}(s)=\max a \in A R_{s}^{a}+\gamma \sum_{s^{\prime} \in S} P_{s, s^{\prime}}^{a} V_{k}\left(s^{\prime}\right) Vk+1(s)=maxa∈ARsa+γs′∈S∑Ps,s′aVk(s′)在策略重复中,我们将以下状态的价值乘以策略函数的概率相加,而在策略重复中,我们贪婪地选择最大的下一个价值。从公式可以看出,只有贝尔是最佳方程。在策略重复中,我们更新了状态价值函数,随后又更新了策略;而在价值重复中,我们没有单独更新策略的步骤。价值循环假定当前的策略是最佳的,并获得最大的补偿。
下面的示例显示了重复值状态价值函数在上述相同示例中的变化情况:

4.2.动态规划的局限性以及为什么需要强化学习
动态规划很难应用于大多数现实世界的问题,其中状态转移概率和奖励函数在现实中无法提前知道,因为必须给出 MDP 的状态转移概率和奖励函数。
这个问题定义得非常好,即使状态转移概率和奖励函数是已知的,随着状态数量的增加,也很难实际求解贝尔曼方程。
这使得很难将动态规划应用于大多数实际问题,其中状态转移概率和奖励函数事先不知道并且状态是无限的。这些缺点可以通过处理强化学习的问题来克服。