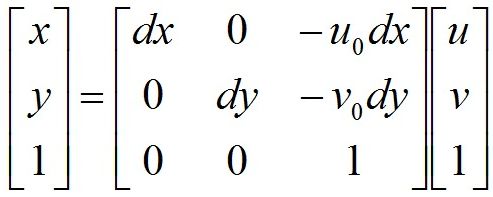【python】Camera Calibration

汇总整理摘抄自

• 相机标定：从世界坐标系到图像像素坐标系转换过程解析
• 四大坐标系与内外参
• 世界坐标系、相机坐标系、图像坐标系之间的关系
• 世界坐标系，相机坐标系，图像坐标系，像素坐标系
• 相机模型 + 世界坐标系+相机坐标系+图像坐标系
• 相机模型中的世界坐标系究竟指什么？
• 老司机帮忙解释下摄像头的世界坐标系？
• 像素坐标系到世界坐标系的转换
• 【相机标定02】从世界坐标系到像素坐标系

---

---

1 坐标系简介

在图像测量过程以及机器视觉应用中，为确定空间物体表面某点的三维几何位置与其在图像中对应点之间的相互关系，必须建立相机成像的几何模型，这些几何模型参数就是相机参数。在大多数条件下这些参数必须通过实验与计算才能得到，这个求解参数（内参、外参、畸变参数）的过程就称之为相机标定（或摄像机标定）。无论是在图像测量或者机器视觉应用中，相机参数的标定都是非常关键的环节，其标定结果的精度及算法的稳定性直接影响相机工作产生结果的准确性。因此，做好相机标定是做好后续工作的前提，提高标定精度是科研工作的重点所在。

确定空间物体表面某点的三维几何位置与其在拍摄图像中对应点之间的相互关系涉及到了如下四个坐标系

• 像素平面坐标系 $(u,v)$

• 像平面坐标系（图像物理坐标系）$(x,y)$

• 相机坐标系 $(X_c,Y_c,Z_c)$，camera coordinate system

• 世界坐标系 $(X_w,Y_w,Z_w)$，world coordinate system (wcs)

我们通过假设一些参数，使上面四个坐标系之间的坐标联系起来，这样我们就可以把拍摄的图片上的一个点坐标反推导出世界坐标系中的那个点坐标，这样就达到了三维重建的目的。

世界坐标系通过平移和旋转（刚体变换）得到相机坐标系。相机坐标系通过成像模型中的相似三角形原理（透视投影）得到图像坐标系。图像坐标系通过平移和缩放得到像素坐标系。

2 图像物理坐标系与像素坐标系

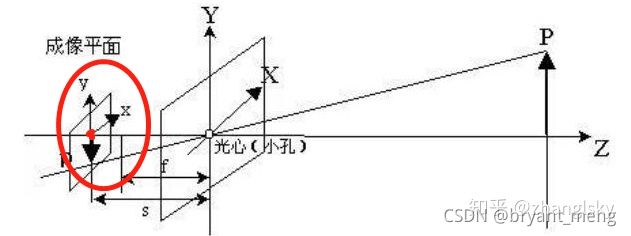
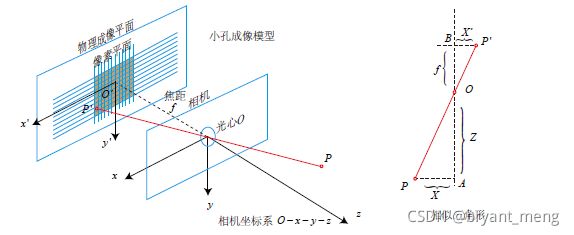
图像物理坐标系 $(x,y)$：以相机光轴与成像平面的交点（principal point）为坐标原点，描述物体通过投影投射在成像平面中的位置（感光芯片上像素的实际大小），单位一般为 mm，属于物理单位。

红色圈出来的区域，即是图像物理坐标系， 红色的原点，可以记为图像坐标系的原点。

像素坐标系 $(u,v)$：以成像平面左上顶点为坐标原点，为了描述像素点（pixel）在数字图像中的坐标位置而引入。

图像坐标系与像素坐标系之间的转换关系如下：

写成矩阵形式：

再写成齐次坐标形式：

其中，$(u,v)$ 表示像素的行数和列数，$(u_0,v_0)$ 表示图像坐标系原点在像素坐标系中的坐标， $dx$ 和 $dy$ 表示单个像素分别在 $x$ 轴和 $y$ 轴上的物理尺寸（单位为 mm/pixel），因而 $\frac{x}{dx}$ 与 $\frac{y}{dy}$的单位为像素。

当然我们也可以表示成如下形式

3 像素坐标系与相机坐标系（内参）

相机坐标系 $(X_c,Y_c,Z_C)$：以相机的光心为坐标原点， [公式] 轴与相机光轴平行，单位为 mm

$Zc$ 是指的图像深度信息，每个像素点的 $Zc$ 都会有差别

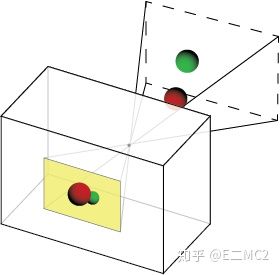
是不是老觉得上面这几幅图和小孔成像背离了，卡看下面这两幅图就柳暗花明，豁然开朗了

红框部分也即

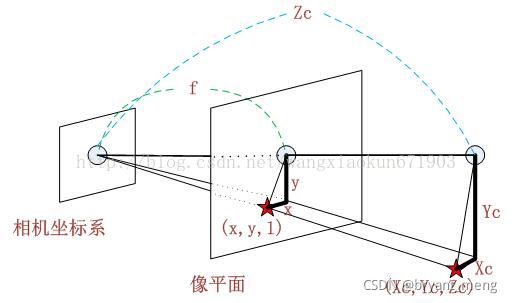
或者直接画成这样就会直观很多

---

根据三角形相似原理可得：

整理可得：

写成齐次坐标矩阵形式：

将像素坐标系与图像坐标系的转换公式带入，可得：

整理可得：

其中，$fx=\frac{f}{dx}$ ， $fy=\frac{f}{dy}$ 分别表示相机在 $x$ 轴和 $y$ 轴方向上的焦距，相机内参（Camera Intrinsic parameter） $K$ 为：

4 相机坐标系与世界坐标系（外参）

世界坐标系 $(X_W,Y_W,Z_W)$：

由于摄像机和物体可以安放在环境中的任何位置，因此需要在环境中选择一个基准坐标系来描述摄像机的位置，并用它来描述环境中任何物体的位置，这个坐标系就叫做世界坐标系。

想将不同视点/视角拍摄的图像信息整合在一起就必须将所有的信息放在同一个坐标系下，这个坐标系应与各张图像的 相机/物体/像素 这些相对坐标系无关，在确定后应不变且唯一，即应为绝对坐标系，我们将这个坐标系称为 世界坐标系 。

世界坐标系可以任意选择，为假想坐标系，在被指定后随即 不变且唯一，即为绝对坐标系

相机坐标的原点，可以是任意的相机位置（如下图黄色框内），一般把相机的光心设置为相机坐标的原点，空间中 Z 轴与摄像机的光轴平行！

世界坐标系与相机坐标系之间为刚体变换的关系：

其中 $\left[\begin{array}{cc}R& T\\ 0& 1\end{array}\right]=\left[\begin{array}{cccc}{r}_{11}& r_{12}& r_{13}& t1\\ r_{21}& r_{22}& r_{23}& t2\\ r_{31}& r_{32}& r_{33}& t3\\ 0& 0& 0& 1\end{array}\right]$

R、T 与摄像机无关，所以称这两个参数为摄像机的外参数 (extrinsic parameter)

下面详细介绍下外参矩阵

因为世界坐标系和像机坐标系都是右手坐标系，所以其不会发生形变。我们想把世界坐标系下的坐标转换到像机坐标下的坐标，如下图所示，可以通过刚体变换的方式。空间中一个坐标系，总可以通过刚体变换转换到另外一个个坐标系的。

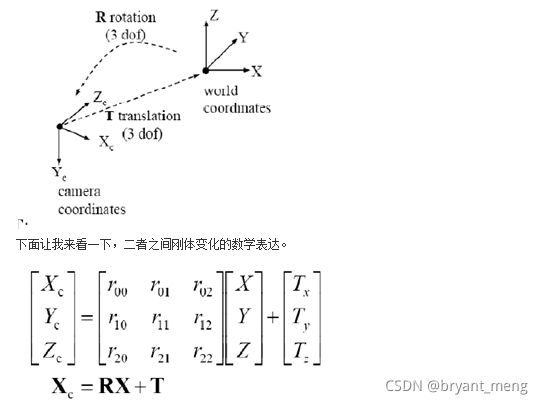
其中，$X_C$ 代表摄像机坐标系，$X$ 代表世界坐标系。$R$ 代表旋转（因其受 x,y,z 三个方向上的分量共同控制，所以其具有三个自由度），$T$ 代表平移

5 实践中，相机世界坐标系的指定

在实践中，世界坐标系的选取可分为两种情况，单目相机与双目相机。

1，单目相机

在单目相机中，我们通常选择拍摄第一张图像时的相机坐标系作为世界坐标系，即以拍摄第一张图像时相机的光心（小孔）作为原点，X 轴为水平方向，Y 轴为竖直方向，Z 轴指向拍摄第一张图像时相机所观察的方向。选定后世界坐标系便不再发生变化，即不变且唯一。

2，双目相机

在双目相机 (A,B) 中，与单目相机大同小异，我们可选取其中一个相机 A 拍摄第一张图像时的相机坐标系为世界坐标系，即以相机 A 拍摄第一张图像时相机的光心（小孔）作为原点，X 轴为水平方向，Y 轴为竖直方向，Z 轴指向拍摄第一张图像时相机 A 所观察的方向。

这样的话 A 相机的 R 为单位矩阵，T 为零向量

A 附录

A1 opencv 库

这里简单的提及一些 opencv 库方法

(1）findChessboardCorners 和 drawChessboardCorners

找标定网格的角点，注意输入需要是灰度图

import cv2
img = cv2.imread(image)
h, w, _ = img.shape
gray = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)
ret, corners = cv2.findChessboardCorners(gray,(w,h),None) # 找角点， w 和 h 是标定表格每行每列的角点个数
cv2.drawChessboardCorners(img,(w,h), corners, ret) # 画角点

参考 python+OpenCV 相机标定

(2）getAffineTransform

根据两张图的三个对应点，求仿射变换矩阵

M = cv2.getAffineTransform(InputArray src, InputArray dst)

• InputArray src：图1的三个点， np.float32([[],[],[]])
• InputArray dstL：图2的三个点， np.float32([[],[],[]])
• M：把图1 转化成图 2 所需的仿射变换矩阵，维度是 2x3

(3）warpAffine

对图片做变换生成新的图片

cv2.warpAffine(src, M, dsize[, dst[, flags[, borderMode[, borderValue]]]]) → dst

• src - 输入图像。
• M - 变换矩阵。
• dsize - 输出图像的大小，（w, h）
• flags - 插值方法的组合（int 类型！）cv2.xxx
• borderMode - 边界像素模式（int 类型！）cv2.xxx
• borderValue - （重点！）边界填充值; 默认情况下，它为0
• dst - 输出图像

参考 OpenCV 之 cv2.getAffineTransform + warpAffine

下面具体看看 flags 和 borderMode 有哪些可供选择的

(4）插值

插值方法，cv2.xxx opencv中插值算法详解

(5）填充

填充方法 python-opencv 图像通道分离，合并，边界扩展

OpenCV库成员——BorderTypes

A2 快门 / 光圈 / 感光度

来自 快门速度、光圈、ISO(感光度)

一个大的光圈(大开口)会通过较多的光线，从而得到更加明亮的照片。小光圈则相反，得到的照片要更暗一点。下图展示了光圈是如何影响曝光的。

光圈变大，景深变小；光圈变小，景深变大。下图展示了使用大光圈和小光圈的区别：

从最基本的来说，ISO 是一种可以使照片变亮或变暗的相机设置。随着 ISO 值的增加，照片会逐渐变亮。 因此，ISO 可以在较暗的环境中拍摄图像，或者更灵活地设置光圈和快门速度。


提高 ISO 是有后果的。在过高的 ISO 下拍摄的照片会显示很多颗粒，也就是噪音，这可能会导致照片无法使用

A3 消除畸变

来自 双目测距理论及其python实现

双目标定 --> 立体校正（含消除畸变） --> 立体匹配 --> 视差计算 --> 深度计算/3D坐标计算

畸变校正

光线经过相机的光学系统往往不能按照理想的情况投射到传感器上，也就是会产生所谓的畸变。畸变有两种情况：一种是由透镜形状引起的畸变称之为径向畸变

在相机的组装过程中由于不能使得透镜和成像面 严格平行也会引入切向畸变

其中 $r^2=x^2+y^2$，x 和 y 均为归一化平面坐标，因此需要得畸变参数总共有5个：

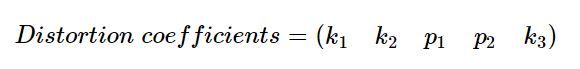
通常来说有这 5 个畸变系数就足够了，对于某些相机来说可能还需要更高阶的参数才能够更精确地建模图像畸变：

其中 s1, s2, s3, s4 是 thin prism distortion coefficients，通过标定可以获得以上所有的畸变参数。opencv 提供了相应的函数做畸变校正

# brief: 消除畸变
# image: 输入图像
# camera_matrix: 相机内参矩阵
# dist_coeff: 相机内参矩阵
undistortion_image = cv2.undistort(image, camera_matrix, dist_coeff)

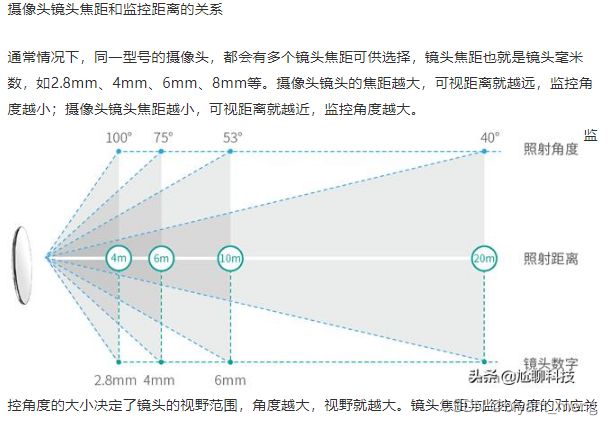
A4 摄像头镜头焦距和监控距离的关系

http://www.360doc.com/content/19/1221/23/3071845_881285502.shtml