利用C#编写一个GPS高程拟合(二次曲面拟合模型)程序
一、代码界面展示
 主要控件包含:groupbox,button,combobox,datagridview,richtextbox
主要控件包含:groupbox,button,combobox,datagridview,richtextbox
二、代码运算结果展示
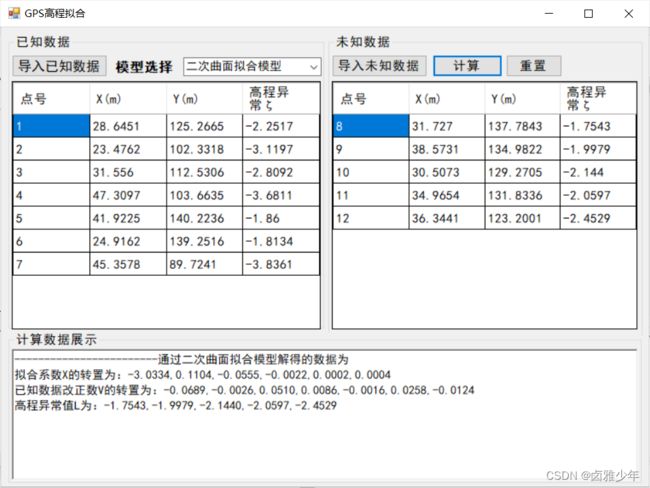
展示一下吧,我实习给的数据直接是高程异常值,不是给的H和h(H是大地高,h是正常高),如果是H和h需要自己增加一些读取的代码,修改一下表格,后面计算公式是一样的。因为高程拟合计算需要使用矩阵,要自己写一个矩阵类,当然CSDN也有很多矩阵库可以借鉴一下。
我之前下载了一个可以进行GPS高程拟合的软件,想对结果进行验证,但是非要购买才能解锁精度,不然那个软件计算结果只能保留整数位,太Crazy了,我就没有验证了,但是我觉得应该没有问题的。不过你可以自己验证验证。
三、源代码
Form1代码
namespace GPS高程拟合
{
public partial class Form1 : Form
{
List<RowData> rdatas = new List<RowData>();
List<UnknownData> udatas = new List<UnknownData>();
Matrix X;
Matrix V;
Matrix L;
double[] RowArrayL;
double[,] RowArrayB;
double[,] UnknowArrayB;
double[] UnknowArrayL;
public Form1()
{
InitializeComponent();
}
private void button1_Click(object sender, EventArgs e)
{
string[] temp;
OpenFileDialog ofd = new OpenFileDialog();
ofd.Filter = "文本文件(*.txt)|*.txt|所有文件(*.*)|*.*";
ofd.Title = "打开数据文件";
//导入txt
if (ofd.ShowDialog(this) == DialogResult.OK)
{
StreamReader sr = new StreamReader(ofd.FileName);
while (!sr.EndOfStream)
{
temp = sr.ReadLine().Split(',');
if (temp.Length!=4)
{
MessageBox.Show("输入数据不完整");
break;
}
RowData rdata = new RowData();
rdata.dh = temp[0];
rdata.x = Convert.ToDouble(temp[1]);
rdata.y = Convert.ToDouble(temp[2]);
rdata.heightanomaly = Convert.ToDouble(temp[3]);
rdatas.Add(rdata);
}
sr.Close();
GridBuild1();
}
else
{
MessageBox.Show("输入失败");
}
}
public void GridBuild1()
{
for (int i = 0; i < rdatas.Count; i++)
{
dataGridView1.Rows.Add();
dataGridView1.Rows[i].Cells[0].Value = rdatas[i].dh;
dataGridView1.Rows[i].Cells[1].Value = rdatas[i].x;
dataGridView1.Rows[i].Cells[2].Value = rdatas[i].y;
dataGridView1.Rows[i].Cells[3].Value = rdatas[i].heightanomaly;
}
}
private void button2_Click_2(object sender, EventArgs e)
{
string[] temp;
OpenFileDialog ofd1 = new OpenFileDialog();
ofd1.Filter = "文本文件(*.txt)|*.txt|所有文件(*.*)|*.*";
ofd1.Title = "打开数据文件";
//导入txt
if (ofd1.ShowDialog(this) == DialogResult.OK)
{
StreamReader sr = new StreamReader(ofd1.FileName);
while (!sr.EndOfStream)
{
temp = sr.ReadLine().Split(',');
UnknownData udata = new UnknownData();
udata.dh = temp[0];
udata.x = Convert.ToDouble(temp[1]);
udata.y = Convert.ToDouble(temp[2]);
udatas.Add(udata);
}
sr.Close();
GridBuild2();
}
else
{
MessageBox.Show("输入失败");
}
}
public void GridBuild2()
{
for (int i = 0; i < udatas.Count; i++)
{
dataGridView2.Rows.Add();
dataGridView2.Rows[i].Cells[0].Value = udatas[i].dh;
dataGridView2.Rows[i].Cells[1].Value = udatas[i].x;
dataGridView2.Rows[i].Cells[2].Value = udatas[i].y;
}
}
private void button3_Click(object sender, EventArgs e)
{
if (comboBox1.Text=="")
{
MessageBox.Show("请选择拟合模型");
}
if ( rdatas.Count == 0 || udatas.Count == 0)
{
MessageBox.Show("未导入完整数据","数据异常");
}
if (comboBox1.Text== "二次曲面拟合模型")
{
RowArrayL = DataImport1().RAL;
RowArrayB = DataImport1().RAB;
UnknowArrayB = DataImport1().unAB;
X = SameCalculationProcess(RowArrayL, RowArrayB, UnknowArrayB).X;
V = SameCalculationProcess(RowArrayL, RowArrayB, UnknowArrayB).V;
L = SameCalculationProcess(RowArrayL, RowArrayB, UnknowArrayB).L;
ShowUnknpwL(L);
richTextBox1.Text += "------------------------通过二次曲面拟合模型解得的数据为" + "\n";
ShowXVL();
}
}
public (double[] RAL, double[,] RAB, double[,] unAB) DataImport1() //二次曲面拟合模型
{
//通过已知数据对X进行求解
RowArrayL = new double[rdatas.Count];
for (int i = 0; i < rdatas.Count; i++)
{
RowArrayL[i] = rdatas[i].heightanomaly;
}
RowArrayB = new double[rdatas.Count, 6];
for (int i = 0; i < rdatas.Count; i++)
{
RowArrayB[i, 0] = 1;
RowArrayB[i, 1] = rdatas[i].x;
RowArrayB[i, 2] = rdatas[i].y;
RowArrayB[i, 3] = rdatas[i].x * rdatas[i].x;
RowArrayB[i, 4] = rdatas[i].x * rdatas[i].y;
RowArrayB[i, 5] = rdatas[i].y * rdatas[i].y;
}
//---------------导入未知点通过X计算高程异常----------------------
UnknowArrayB = new double[udatas.Count, 6];
for (int i = 0; i < udatas.Count; i++)
{
UnknowArrayB[i, 0] = 1;
UnknowArrayB[i, 1] = udatas[i].x;
UnknowArrayB[i, 2] = udatas[i].y;
UnknowArrayB[i, 3] = udatas[i].x * udatas[i].x;
UnknowArrayB[i, 4] = udatas[i].x * udatas[i].y;
UnknowArrayB[i, 5] = udatas[i].y * udatas[i].y;
}
return (RowArrayL, RowArrayB, UnknowArrayB);
}
public (Matrix X, Matrix V,Matrix L) SameCalculationProcess(double[] RowArrayL,double[,] RowArrayB,double[,] unknowArrayB )
{
Matrix L1 = new Matrix(1, rdatas.Count, RowArrayL);
Matrix L = L1.Transpose();//-------------------------------L矩阵
Matrix B = new Matrix(RowArrayB);//-------------------------------B矩阵
Matrix BT = B.Transpose();//------------------------------BT矩阵
Matrix X = BT.Multiply(B);
X.InvertGaussJordan();//-------------------------------求逆直接改变X的值,不需要赋值
Matrix X2 = X.Multiply(BT);
Matrix X3 = X2.Multiply(L);//-------------------------------X的最终解
//--------V=BX-L---------
Matrix V1 = B.Multiply(X3);
Matrix V = V1.Subtract(L);//-----------------------V改正值
Matrix B3 = new Matrix(unknowArrayB);
Matrix L3 = B3.Multiply(X3);//----------------计算结果
//V为改正数;L3为高程异常值;X为拟合系数;B3为系数矩阵。
return (X3, V,L3);
}
public void ShowXVL() {
richTextBox1.Text += "拟合系数X的转置为:" + X.Transpose().ToString() + "\n";
richTextBox1.Text += "已知数据改正数V的转置为:" + V.Transpose().ToString() + "\n";
richTextBox1.Text += "高程异常值L为:" + L.Transpose().ToString() + "\n";
}
public void ShowUnknpwL(Matrix L)
{
UnknowArrayL = L.GetData();
for (int i = 0; i < udatas.Count; i++)
{
dataGridView2.Rows[i].Cells[3].Value = Math.Round(UnknowArrayL[i], 4);
}
}
private void Form1_Load(object sender, EventArgs e)
{
}
private void dataGridView2_CellContentClick(object sender, DataGridViewCellEventArgs e)
{
}
private void richTextBox1_TextChanged(object sender, EventArgs e)
{
}
private void label1_Click(object sender, EventArgs e)
{
}
private void button4_Click(object sender, EventArgs e)
{
dataGridView1.Rows.Clear();
dataGridView2.Rows.Clear();
richTextBox1.Text = "";
rdatas.Clear();
udatas.Clear();
}
private void comboBox1_SelectedIndexChanged(object sender, EventArgs e)
{
}
}
}
Data类(变量)
namespace GPS高程拟合
{
class RowData//原始数据
{
public string dh;
public double x;
public double y;
public double heightanomaly;//高程异常
}
class UnknownData//未知数据
{
public string dh;
public double x;
public double y;
}
}
矩阵类(其他需要矩阵的运算的也可以用,也可以直接增添方法)
namespace GPS高程拟合
{
public class Matrix
{
private int numColumns = 0; // 矩阵列数
private int numRows = 0; // 矩阵行数
private double[] elements = null; // 计算的临时数据
public int Columns
{ //属性: 矩阵列数
get { return numColumns; }
}
public int Rows
{ //属性: 矩阵行数
get { return numRows; }
}
public double this[int row, int col]
{ // 访问矩阵元素
get
{ return elements[col + row * numColumns]; }
set
{ elements[col + row * numColumns] = value; }
}
public Matrix(int nRows, int nCols)
{ //指定行列构造函数
numRows = nRows;
numColumns = nCols;
Init(numRows, numColumns);
}
public Matrix(double[,] value)
{ //指定值(二维数组)构造函数
numRows = value.GetLength(0);
numColumns = value.GetLength(1);
double[] data = new double[numRows * numColumns];
int k = 0;
for (int i = 0; i < numRows; ++i)
for (int j = 0; j < numColumns; ++j)
data[k++] = value[i, j];
Init(numRows, numColumns);
SetData(data);
}
public Matrix(int nRows, int nCols, double[] value)
{ //指定值(一位数组)构造函数
numRows = nRows;
numColumns = nCols;
Init(numRows, numColumns);
SetData(value);
}
public Matrix(Matrix other)
{ //拷贝构造函数
numColumns = other.GetNumColumns();
numRows = other.GetNumRows();
Init(numRows, numColumns);
SetData(other.elements);
}
public bool Init(int nRows, int nCols)
{ //初始化函数
numRows = nRows;
numColumns = nCols;
int nSize = nCols * nRows;
if (nSize < 0)
return false;
elements = new double[nSize];
return true;
}
public override string ToString()
{ //将矩阵各元素的值转化为字符串, 元素之间的分隔符为",", 行与行之间有回车换行符
return ToString(",", true);
}
//将矩阵各元素的值转化为字符串
public string ToString(string sDelim, bool bLineBreak)
{
string s = "";
for (int i = 0; i < numRows; ++i)
{
for (int j = 0; j < numColumns; ++j)
{
string ss = GetElement(i, j).ToString("F4");
s += ss;
if (bLineBreak)
{
if (j != numColumns - 1)
s += sDelim;
}
else
{
if (i != numRows - 1 || j != numColumns - 1)
s += sDelim;
}
}
if (bLineBreak)
if (i != numRows - 1)
s += "\r\n";
}
return s;
}
//设置矩阵各元素的值,一维数组,长度为numColumns*numRows,存储
public void SetData(double[] value)
{
elements = (double[])value.Clone();
}
public bool SetElement(int nRow, int nCol, double value)
{
if (nCol < 0 || nCol >= numColumns || nRow < 0 || nRow >= numRows)
return false;
elements[nCol + nRow * numColumns] = value;
return true;
}
public double GetElement(int nRow, int nCol)
{ //获取指定元素的值
return elements[nCol + nRow * numColumns];
}
public int GetNumColumns()
{ //获取矩阵的列数
return numColumns;
}
public int GetNumRows()
{ //获取矩阵的行数
return numRows;
}
public double[] GetData()
{ //获取矩阵的数据
return elements;
}
public Matrix Add(Matrix other)
{ //实现矩阵的加法
if (numColumns != other.GetNumColumns() ||
numRows != other.GetNumRows())
throw new Exception("矩阵的行/列数不匹配。");
// 构造结果矩阵
Matrix result = new Matrix(this);
// 矩阵加法
for (int i = 0; i < numRows; ++i)
for (int j = 0; j < numColumns; ++j)
result.SetElement(i, j, result.GetElement(i, j) + other.GetElement(i, j));
return result;
}
public Matrix Subtract(Matrix other)
{ //实现矩阵的减法
if (numColumns != other.GetNumColumns() ||
numRows != other.GetNumRows())
throw new Exception("矩阵的行/列数不匹配。");
// 构造结果矩阵
Matrix result = new Matrix(this);
// 进行减法操作
for (int i = 0; i < numRows; ++i)
for (int j = 0; j < numColumns; ++j)
result.SetElement(i, j, result.GetElement(i, j) - other.GetElement(i, j));
return result;
}
public Matrix Multiply(Matrix other)
{ //实现矩阵的乘法
if (numColumns != other.GetNumRows())
throw new Exception("矩阵的行/列数不匹配。");
Matrix result = new Matrix(numRows, other.GetNumColumns());
double value;
for (int i = 0; i < result.GetNumRows(); ++i)
{
for (int j = 0; j < other.GetNumColumns(); ++j)
{
value = 0.0;
for (int k = 0; k < numColumns; ++k)
{
value += GetElement(i, k) * other.GetElement(k, j);
}
result.SetElement(i, j, value);
}
}
return result;
}
public Matrix Transpose()
{ //矩阵的转置
Matrix Trans = new Matrix(numColumns, numRows);
// 转置各元素
for (int i = 0; i < numRows; ++i)
{
for (int j = 0; j < numColumns; ++j)
Trans.SetElement(j, i, GetElement(i, j));
}
return Trans;
}
public bool InvertGaussJordan()
{ //矩阵求逆
int i, j, k, l, u, v;
double d = 0, p = 0;
// 分配内存
int[] pnRow = new int[numColumns];
int[] pnCol = new int[numColumns];
// 消元
for (k = 0; k <= numColumns - 1; k++)
{
d = 0.0;
for (i = k; i <= numColumns - 1; i++)
{
for (j = k; j <= numColumns - 1; j++)
{
l = i * numColumns + j; p = Math.Abs(elements[l]);
if (p > d)
{
d = p;
pnRow[k] = i;
pnCol[k] = j;
}
}
}
// 失败
if (d == 0.0)
{
return false;
}
if (pnRow[k] != k)
{
for (j = 0; j <= numColumns - 1; j++)
{
u = k * numColumns + j;
v = pnRow[k] * numColumns + j;
p = elements[u];
elements[u] = elements[v];
elements[v] = p;
}
}
if (pnCol[k] != k)
{
for (i = 0; i <= numColumns - 1; i++)
{
u = i * numColumns + k;
v = i * numColumns + pnCol[k];
p = elements[u];
elements[u] = elements[v];
elements[v] = p;
}
}
l = k * numColumns + k;
elements[l] = 1.0 / elements[l];
for (j = 0; j <= numColumns - 1; j++)
{
if (j != k)
{
u = k * numColumns + j;
elements[u] = elements[u] * elements[l];
}
}
for (i = 0; i <= numColumns - 1; i++)
{
if (i != k)
{
for (j = 0; j <= numColumns - 1; j++)
{
if (j != k)
{
u = i * numColumns + j;
elements[u] = elements[u] - elements[i * numColumns + k] * elements[k * numColumns + j];
}
}
}
}
for (i = 0; i <= numColumns - 1; i++)
{
if (i != k)
{
u = i * numColumns + k;
elements[u] = -elements[u] * elements[l];
}
}
}
// 调整恢复行列次序
for (k = numColumns - 1; k >= 0; k--)
{
if (pnCol[k] != k)
{
for (j = 0; j <= numColumns - 1; j++)
{
u = k * numColumns + j;
v = pnCol[k] * numColumns + j;
p = elements[u];
elements[u] = elements[v];
elements[v] = p;
}
}
if (pnRow[k] != k)
{
for (i = 0; i <= numColumns - 1; i++)
{
u = i * numColumns + k;
v = i * numColumns + pnRow[k];
p = elements[u];
elements[u] = elements[v];
elements[v] = p;
}
}
}
// 成功返回
return true;
}
}
}
四、结语
主要难度还是在矩阵的编写,不会写也没关系,用别人写的也行。
我的其他文章:
- 利用Python编写一个高斯正反算程序:https://blog.csdn.net/Zj1638/article/details/125740379
- 利用C#编写一个高斯正反算程序:https://blog.csdn.net/Zj1638/article/details/125380593
- 利用C#编写一个水准测量近似平差程序:https://blog.csdn.net/Zj1638/article/details/119303957
- 利用C#编写一个附和闭合导线简易平差程序:https://blog.csdn.net/Zj1638/article/details/125639541
相关下载链接:
- 利用C#编写一个水准测量近似平差程序下载链接:https://download.csdn.net/download/Zj1638/16732130
- 利用C#编写一个附和闭合导线简易平差程序下载链接:https://download.csdn.net/download/Zj1638/85928040
- 利用C#编写一个高斯正反算程序下载链接:https://download.csdn.net/download/Zj1638/85711234
- 利用Python编写一个高斯正反算程序下载链接:https://download.csdn.net/download/Zj1638/86059069
- 利用C#编写一个GPS高程拟合(二次曲面拟合模型)程序下载链接:https://download.csdn.net/download/Zj1638/85916113
需要的可以支持一下。如果有什么不懂的,可以私信,我看到了会回答的。