李宏毅老师-self-attention笔记
本文部分内容参考于以下博客:
自注意力机制
文章目录
- 自注意力输入和输出
- 自注意力机制函数
- self_attention的计算过程
- self_attention的矩阵表示方法:
- 多头注意力机制
- 位置编码
自注意力输入和输出
1.自注意力模型
输入的序列是变长的序列,输出的是一个标量

2.输入和输出都是序列,而且输入和输出的长度相等,输入的每一个元素对应输出的一个label。

3.输出序列的长度是不定的,这种情况其实也就是Seq2Seq模型,比如机器翻译。如下图所示:
4.输出序列的长度为1,此时相当于一个分类人物,比如像对正面/负面评论的分析

自注意力机制函数
由于需要建立输入向量序列的依赖关系,因此模型要考虑整个输入序列的信息,之后将输出向量输入到full-connected,做后续处理。

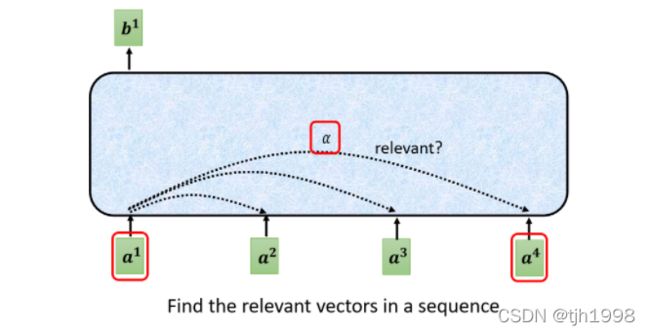
之前提到过,self_attention研究的是target或者source元素之间的相关性,假设此时的被查询的元素是 a 1 a^1 a1,我们计算 a 1 和 a 1 , a 2 , a 3 , a 4 a^1和a^1,a^2,a^3,a^4 a1和a1,a2,a3,a4之间的相关性,这样做的好处是不需要把所有的信息都输入到神经网络中,只需要从X中选择和任务相关的信息即可。
计算相关度的函数有以下2种:

输入的两个向量,通过和权重矩阵 W q 和 W k 相 乘 得 到 q 和 k , q 和 k W^q和W^k相乘得到q和k,q和k Wq和Wk相乘得到q和k,q和k进行内积(对应元素相乘并相加的方式)从而求相关性 α \alpha α.
另外的方式:
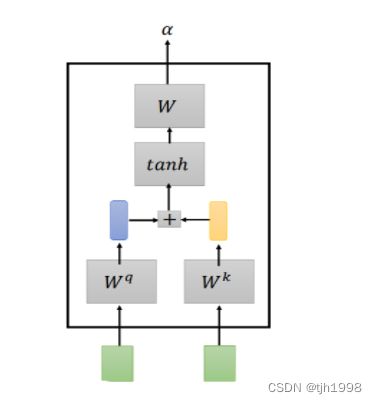
输入的两个向量,通过和权重矩阵 W q 和 W k W^q和W^k Wq和Wk相乘得到 q q q和 k k k,之后将 q q q和 k k k串联输入到一个激活函数( t a n h tanh tanh)中,通过一个transform得到 α \alpha α
self_attention的计算过程
一般来说,我们通过(key,value)的方式来表示输入信息,其中key用来计算注意力分布 α n \alpha_n αn,而value用来计算聚合信息,通常情况下:key值和value值是一样的。query代表的是被查询的向量。
如下图所示:a1为被查询向量,计算 a 1 与 [ a 2 , a 3 , a 4 ] a1与[a2,a3,a4] a1与[a2,a3,a4]的关联性α(实践时一般也会计算与a1自己的相关性)。以Dot-product为例,我们分别将 [ a 1 , a 2 ] , [ a 1 , a 3 ] , [ a 1 , a 4 ] [a1,a2],[a1,a3],[a1,a4] [a1,a2],[a1,a3],[a1,a4]作为Dot-product的输入,求得对应的相关性 [ α 11 , α 12 , α 13 , α 14 ] [\alpha11,α12,α13,α14] [α11,α12,α13,α14]

2.计算出来a1跟每一个向量的关联性之后,将得到的关联性输入的softmax中,这个softmax和分类使用的softmax时一样的,得到对应数量的α′。
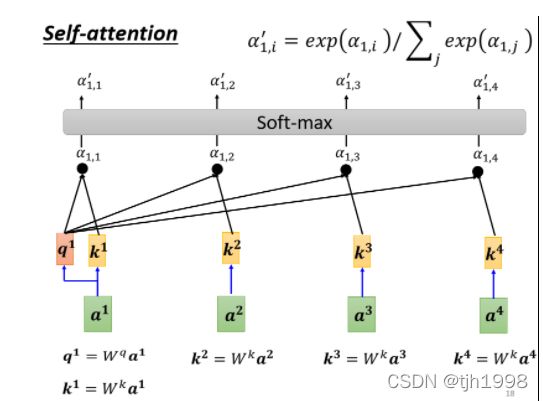
3.将a1,a2,a3,a4乘以权重矩阵 W v W^v Wv得到对应的value值,之后对应的 v i v^i vi和之前计算出来的 α 1 , i ′ \alpha'_{1,i} α1,i′对应相乘再相加,即可得到注意力分数。
self_attention的矩阵表示方法:
这里输入的向量依旧是[a1,a2,a3,a4],对应的输入向量[a1,a2,a3,a4]拼接到一起组成I数组,对应的 [ q 1 = W q a 1 , q 2 = W q a 2 , q 3 = W q a 3 , q 4 = W q a 4 ] [q1=W^qa^1,q2=W^qa^2,q3=W^qa^3,q4=W^qa^4] [q1=Wqa1,q2=Wqa2,q3=Wqa3,q4=Wqa4]拼接在一起,得到Q矩阵。同理K和V矩阵也是同样获得的。

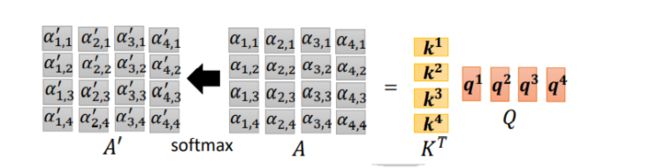
2.得到Q,K,V矩阵之后,下一步由Q和K计算相关性,以计算q1为例子,使用q1和[k1,k2,k3,k4]分别相乘得到了[ α 11 , α 12 , α 13 , α 14 \alpha_{11},\alpha_{12},\alpha_{13},\alpha_{14} α11,α12,α13,α14],为了使用矩阵的乘法运算,对[k1,k2,k3,k4]进行转置,再和q1相乘。转置之后: K T K^T KT的矩阵是 4 ∗ 1 4*1 4∗1的, q 1 q^1 q1是 1 ∗ 1 1*1 1∗1可以直接相乘。

3.将第一步得到的K矩阵进行转置,得到 K T K^T KT。K和Q相乘,得到相关矩阵A,A再经过softmax函数,得到归一化的矩阵 A ′ A' A′
如下图所示: K T K^T KT是一个 4 ∗ 1 4*1 4∗1的矩阵,而Q矩阵是一个 1 ∗ 4 1*4 1∗4的矩阵,可以进行矩阵的运算。

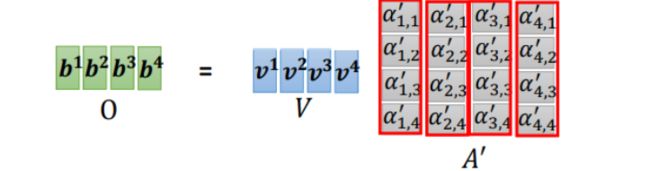
我们将矩阵V依次乘以矩阵A′中的每一列得到输出[b1,b2,b3,b4]

综上所述:计算过程如下所示
- 计算Q,K,V三个矩阵。
Q = W q I , K = W k I , V = W v I Q=W^qI,K=W^kI,V=W^vI Q=WqI,K=WkI,V=WvI - 计算Q和V的相似度,经过softmax函数进行归一化得到注意力矩阵 A ′ A' A′
A = K T Q , A ′ = s o f t m a x ( A ) A=K^TQ,A'=softmax(A) A=KTQ,A′=softmax(A) - 计算输出矩阵: O = V A ′ O=VA' O=VA′
注意,一般情况下,V的取值等于K等于输入向量,故而 V ∗ A ′ 计 算 的 V*A'计算的 V∗A′计算的是输入信息的加权平均值。
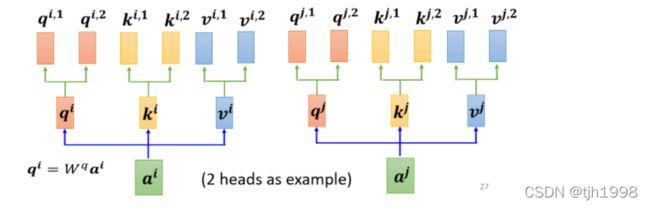
多头注意力机制
多头注意力(Multi-Head Attention)是利用多个查询 Q = [ q 1 , q 2 , . . . , q m ] Q=[q1,q2,...,qm] Q=[q1,q2,...,qm]来并行地从输入信息中选取多组信息.每个注意力关注输入信息的不同部分。
在Self-Attention中,我们是使用q去寻找与之相关的k,但是这个相关性并不一定有一种。那多种相关性体现到计算方式上就是有多个矩阵q,不同的q负责代表不同的相关性。
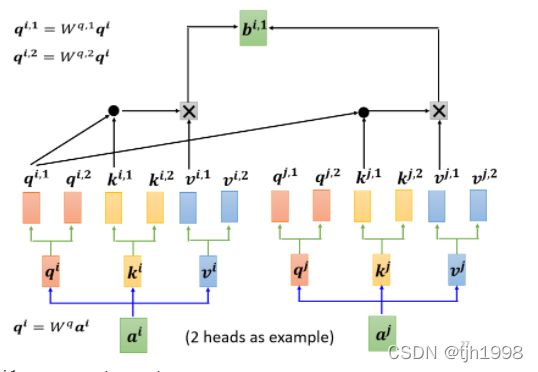
这里展现的是两个head的,首先利用a和 W q W^q Wq相乘得到了 q i q^i qi,之后 q i q^i qi再乘以两个权重矩阵得到qi,1和qi,2。
1. q i 1 只 和 k i 1 , k j 1 qi1只和ki1,kj1 qi1只和ki1,kj1进行相似度运算得到 α i 1 和 α j 1 \alpha{i1}和\alpha{j1} αi1和αj1,而不需要和 k i 2 和 k j 2 ki2和kj2 ki2和kj2进行相似度的计算。
2.得到的结果再和 v i , 1 和 v j , 1 v^{i,1}和v^{j,1} vi,1和vj,1进行相乘再相加,从而可以得到 b i , 1 b^{i,1} bi,1。相同的方法可以得到 b i , 2 b^{i,2} bi,2
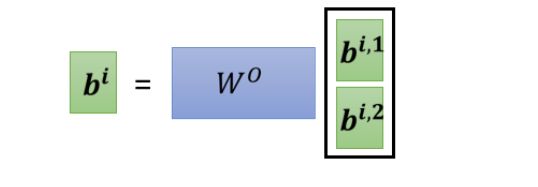
3.将 b i , 1 和 b i , 2 b^{i,1}和b^{i,2} bi,1和bi,2拼接起来,乘以一个权重矩阵 W O W^O WO,得到最终的输出 b i b^i bi
位置编码
我们可以发现对于每一个input是出现在sequence的最前面,还是最后面这样的位置信息,Self-Attention是无法获取到的。这样子可能会出现一些问题,比如在做词性标记(POS tagging)的时候,像动词一般不会出现在句首的位置这样的位置信息还是非常重要的。
我们可以使用positional encoding的技术,将位置信息加入到Self-Attention中。

如上图所示,我们可以为每个位置设定一个专属的positional vector,用ei表示,上标i代表位置。我们先将ei和ai相加,然后再进行后续的计算就可以了。ei向量既可以人工设置,也可以通过某些function或model来生成。