pytorch 常见的网络层(卷积层,池化层,线性层,激活函数)
卷积层
卷积运算:卷积核在图像上滑动,相应位置进行乘加;
卷积层:又称为滤波器,过滤器,可以认为是某种模式,某种特征。
卷积的过程类似于用一个模版去图像上寻找与它相似的区域,与卷积模式越相似,激活值越高,从而实现特征的提取。
一般情况下,卷积核在几维上滑动就是几维卷积
二维卷积示意图
![]()
二维卷积(多通道版本)
如果是多个通道的卷积核,首先按照单个通道进行操作,然后将得到的多个通道的特征图进行相加得到最后的结果。如下图:输入特征是3个通道的,那么单个卷积核也是三个通道的,首先进行卷积然后将多个通道的卷积进行相加。![]()
![]()
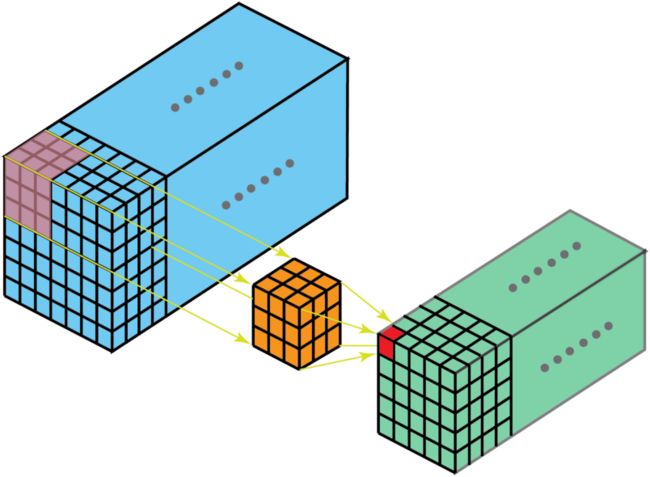
三维卷积
三维卷积有点类似于上面的二维卷积的多通道版本。但是这是完全不同的。二维卷积卷积核是二维的,输入图像存在通道这个维度,类似于二维卷积,三维卷积的卷积核是三维的,如果在存在一个维度那么输入图像其实是四维的。
空洞卷积
为扩大感受野,在卷积核里面的元素之间插入空格来“膨胀”内核,形成空洞卷积。
用膨胀率参数L表示要扩大内核的范围,即在内核元素之间插入L-1个空格。当L=1时,则内核元素之间没有插入空格,变为标准卷积。
下图为L=2的空洞卷积
![]()
可分离卷积
空间可分离卷积
空间可分离卷积是将卷积核分解为两项独立的核分别进行操作
![]()
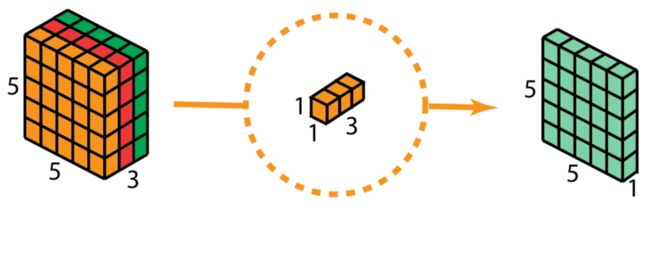
深度可分离卷积
深度可分离卷积由两步组成:深度卷积和1x1卷积。
深度可分离卷积首先是进行深度卷积,将输入按照通道分成每一份,那么每个卷积核变成单通道的了,进行卷积之后然后进行堆叠。
详细请看深度可分离卷积
然后在进行 1x1卷积。
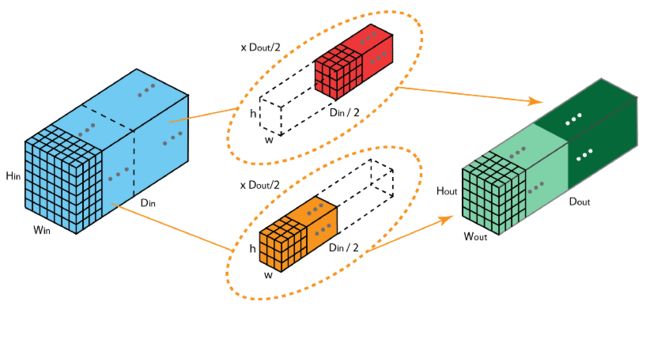
分组卷积
2012年,AlexNet论文中最先提出来的概念,当时主要为了解决GPU显存不足问题,将卷积分组后放到两个GPU并行执行。
在分组卷积中,卷积核被分成不同的组,每组负责对相应的输入层进行卷积计算,最后再进行合并。
混洗分组卷积(Shuffled Grouped Convolution)
在分组卷积中,卷积核被分成多个组后,输入层卷积计算的结果仍按照原先的顺序进行合并组合,这就阻碍了模型在训练期间特征信息在通道组之间流动,同时还削弱了特征表示。而混洗分组卷积,便是将分组卷积后的计算结果混合交叉在一起输出
反卷积
卷积是对图像提取特征,图像的尺寸会变小。
反卷积是图像进行上采样。
![]()
池化层
池化运算:对信号进行“收集” 并“总结
常见的池化操作有最大池化,平均池化。
nn.Maxpool2()对二维信号(图像)进行最大值池化
nn.MaxPool2d(kernel_size, stride=None, padding=0, dilation=1, return_indices=False, ceil_mode=False)
nn.MaxUnpool2d()对二维信号(图像)进行最大值池化上采样
nn.AvgPool2d() 对二维信号(图像)进行平均值池化
线性层
线性层又称为全连接层,其每个神经元与上一层所有神经元相连,实现对前一层的线性组合,线性变换.
nn.Linear(in_features, out_features, bias=True)
对一维向量(信号)进行线性组合
激活函数层
不使用激活函数的话,神经网络的每层都只是做线性变换,多层叠加后还是线性变换。因为线性模型的表达能力通常不够,所以引入激活函数,加入非线性因素,来增强模型的表达能力。
常见的激活函数
Sigmoid激活函数
sigmoid激活函数,它将一个实数值压缩到0至1范围内,
sigmoid函数的主要缺点:
- 梯度消失:当输入很大或很小时,sigmoid的梯度为0,所以会导致梯度消失。
- 不是0均值:sigmoid函数输出不是0均值的
- 计算量太大:指数函数与其他非线性激活函数相比,计算量太大
Tanh激活函数
tanh也是把实数值进行压缩,它将输出值压缩到-1到1之间,输出是0均值的,可以将tanh看作两个sigmoid加在一起的。
优点:输出是0均值
缺点:存在梯度消失问题,指数函数计算量大
ReLu
优点:
● Relu解决了梯度消失问题,至少在正区间内,神经元不会饱和;
● 运算速度快,Relu只是线性关系,不需要指数运算,不管向前传播还是反向传播,速度要比sigmoid和tanh快。
缺点:
● Relu输出不是零均值;
● 随着训练的进行,会出现权值无法更新,神经元死亡的问题。
Leaky Relu
为了解决relu激活函数在x<0时的梯度消失问题,引入Leaky Relu
优点:
● 神经元不会出现死亡问题;
● 对于所有的输入,不管是大于0还是小于等于0,神经元不会饱和;
● 计算速度快,由于只有线性计算,不需要指数运算,无论是正向传播还是反向传播,计算速度都要比sigmoid和tanh快。
缺点:Leaky ReLU函数中的α,需要通过先验知识人工赋值。
PRelu
RReLU的英文全称是“Randomized Leaky ReLU”,中文名字叫“随机修正线性单元”。RReLU是Leaky ReLU的随机版本。
特点:
- RReLU是Leaky ReLU的random版本,在训练过程中,α是从一个高斯分布中随机出来的,然后再测试过程中进行修正。
- 数学形式与PReLU类似,但RReLU是一种非确定性激活函数,其参数是随机的
ELU
指数线性单元。
优点:
● ELU包含了ReLU的所有优点。
● 神经元不会出现死亡的情况。
● ELU激活函数的输出均值是接近于零的。
缺点:计算的时候是需要计算指数的,计算效率低的问题。
参考文献:
【图解AI:动图】各种类型的卷积,你认全了吗? - 雪饼的个人空间 - OSCHINA - 中文开源技术交流社区pytorch学习笔记八:nn网络层——激活函数层_Dear_林的博客-CSDN博客_pytorch 激活层