一种基于迭代傅里叶变换算法纯相位全息图的优化
一、原理
可以生成纯相位全息图的迭代算法中,迭代傅立叶变换算法(Iterative Fourier TransformAlgorithm,IFTA)是一种比较具有代表性的算法,该类算法的特点是通过傅立叶变换在两个平面中的反复传递。迭代傅立叶变换算法,或称误差减少算法(Error Reduction Algorithm)在20世纪70年代早期被作为数字全息的一种算法而提出,后来被Gerchberg与Saxton修改并运用在相位提取领域,成为了迭代算法中最著名也可能是被运用最多的方法–Gerchberg-Saxton(GS)算法。该算法中,根据全息图平面与重建图像平面的振幅分布,通过迭代进行正逆向的光波传递以及施加在两个平面上的限制条件(Constraint),进而求得全息图平面中光场的相位信息。该方法在计算纯相位全息图场景中十分适用,可以使用菲涅尔变换或者傅立叶变换来进行光场传播的计算[1]。
在生成纯相位全息图 H p ( x , y ) {{H}_{p}}\left( x,y \right) Hp(x,y)时,重构像的幅值必须正比于理想幅值分布A(x,y),即
F { H p ( x , y ) } = F { e − j ϕ ( x , y ) } = A ( x , y ) e − j θ ( x , y ) F\left\{ {{H}_{p}}\left( x,y \right) \right\}=F\left\{ {{e}^{-j\phi \left( x,y \right)}} \right\}=A\left( x,y \right){{e}^{-j\theta \left( x,y \right)}} F{Hp(x,y)}=F{e−jϕ(x,y)}=A(x,y)e−jθ(x,y)
式中, ϕ ( x , y ) \phi \left( x,y \right) ϕ(x,y)是全息图的相位; θ ( x , y ) \theta \left( x,y \right) θ(x,y)是重构光场的相位。在设计纯相位CGH时,需要找到相位函数 θ ( x , y ) \theta \left( x,y \right) θ(x,y),使得 H p {{H}_{p}} Hp变成纯相位函数。基于这一思想,IFTA是一种寻找 θ ( x , y ) \theta \left( x,y \right) θ(x,y)的最优解的算法。
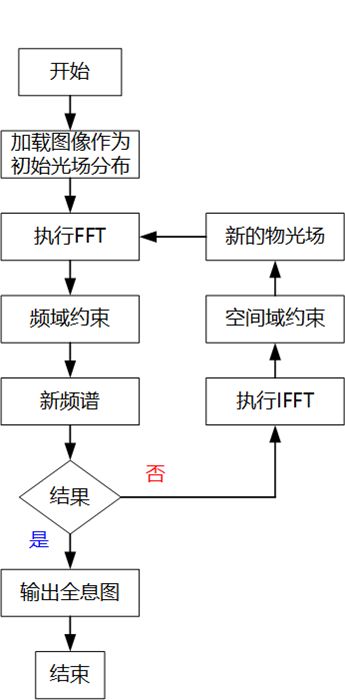
图1为IFTA生成全息图的常用流程图。首先,加载初始条纹作为目标重构光场的幅值(模)分布A(x,y)。。如果需要,也可以在输入条纹中加入相位掩模,作为初始光场。初始光场经变换至频谱域,根据约束条件修正频谱。在该问题中,约束条件谱的模必须是均匀的。于是设频谱的模为单位1,相位不变。修改后的频谱逆变换到空间域。然后利用空间域光场的约束条件,从而获得新的光场。在该问题中,空间域的限制条件是给定的模分布A(x,y),因此强制光场的模为A(x,y),保留相位不变。然后,得到的光场被看作下次迭代中的初始光场。重复迭代过程,直至达到所需目标(如一定迭代次数)。
二、实例分析
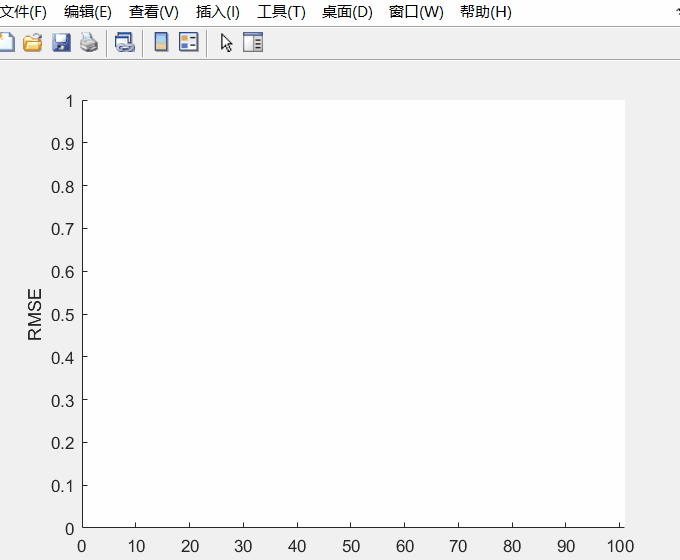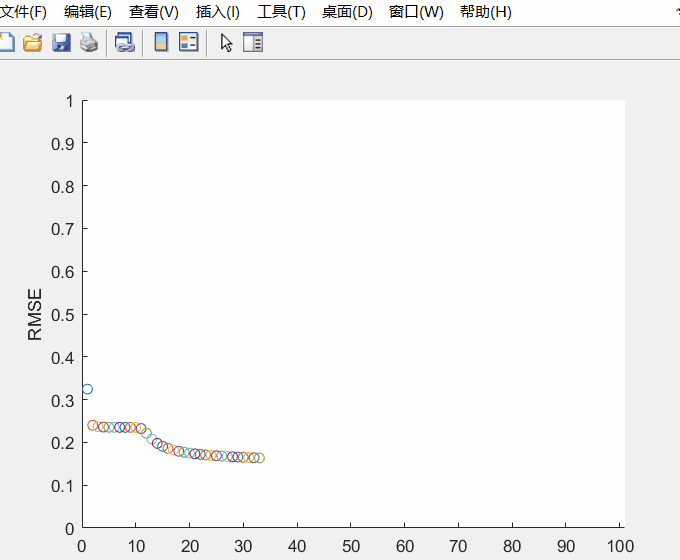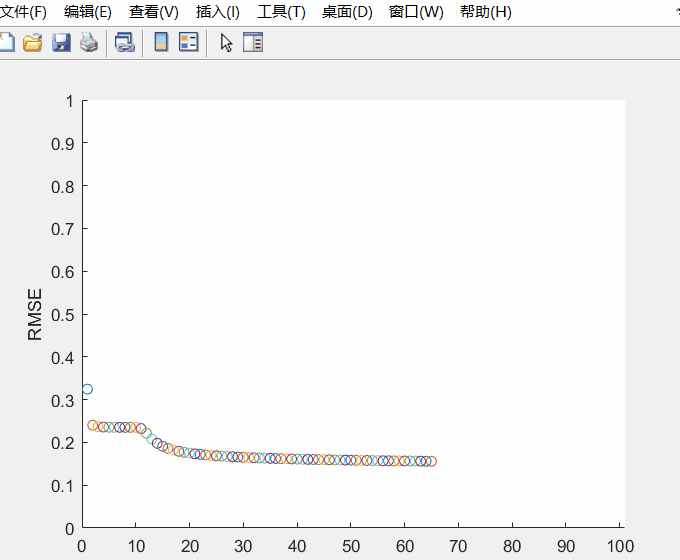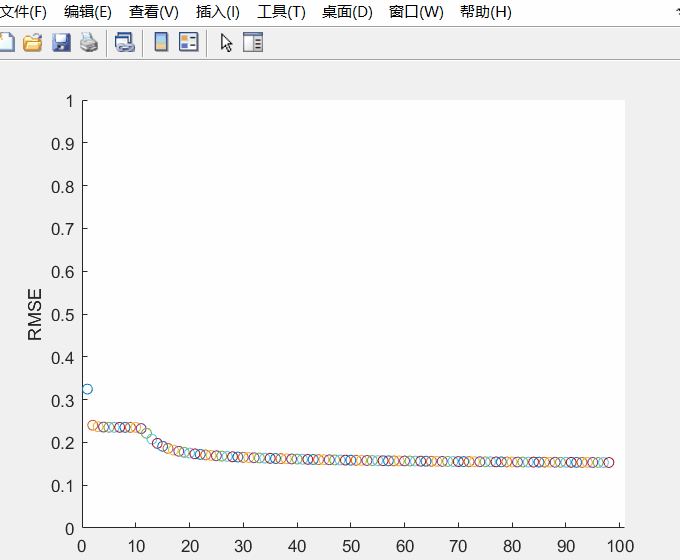
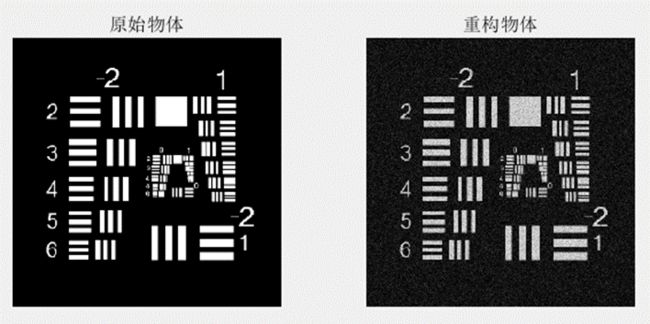
首先,初始输入图像变换到频谱域,提取出相位谱然后变换回空间域。为评价全息图重构质量,可计算均方根误差(RMSE),其定义为
R M S E = { 1 M N ∑ m , n [ ∣ ψ ( m , n ) ∣ − A ( m , n ) ] 2 } 0.5 RMSE={{\left\{ \frac{1}{MN}\sum\limits_{m,n}{{{\left[ \left| \psi (m,n) \right|-A(m,n) \right]}^{2}}} \right\}}^{0.5}} RMSE={MN1m,n∑[∣ψ(m,n)∣−A(m,n)]2}0.5
式中, A ( m , n ) A(m,n) A(m,n)是目标图像; ψ ( m , n ) \psi (m,n) ψ(m,n)是待评价的光场;(m,n)为采样点指标;M、N分别是x轴、y轴的采样数目。
RMSE随迭代次数的变化情况如下动图所示,总的迭代次数是100。随着迭代次数增加,误差逐渐减小。
参考文献
[1] 卜浩祯, 焦述铭. 纯相位全息图优化算法[J]. 液晶与显示, 2021, 36(06): 810-826.
资源获取
上述资源可从以下链接处获取:
https://download.csdn.net/download/qq_36584460/85077528
如有任何疑问,可私信博主。