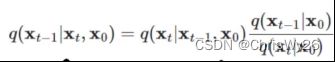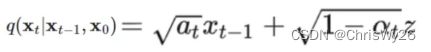stable diffusion原理
1、Latent space
隐空间是压缩数据的一个表示。数据压缩的目的是学习数据中较重要的信息。以编码器-解码器网络为例,首先使用全卷积神经网(FCN)络学习图片特征,我们将特征提取中对数据的降维看作一种有损压缩。但是由于解码器需要重建(reconstruct)数据,所以模型必须学习如何储存所有相关信息并且忽略噪音。所以压缩(降维)的好处在于可以去掉多余的信息从而关注于最关键的特征。
2、AutoEncoder 和 VAE
AutoEncoder:
(1)AE是一个预训练的自编码器,自编码器的目的是数据降维,其优化目标是通过编码器压缩数据,再通过解码器还原数据,使得输入输出的数据尽量相同
(2)理论上来说对于图像数据,解码器还原数据可以看做是一个生成器的功能,由于解码器的输入数据z属于R空间,输入z的分布无法被固定住,所以大部分生成的图片是无意义的。
VAE:
(1)给定输入解码器的z一个分布可以解决上述问题,假设一个服从标准多元高斯分布的多维随机变量的数据集X,通过根据已知分布采样得到的zi,来训练decoder神经网络,从而得到多元高斯分布的均值和方差,从而成功得到一个逼近真实分布p(X)的p’(X)
(2)求解p’(X|z)的概率分布
(3)通过极大似然估计,最大化p’(X)的概率,但由于xi的维度很大,zi的维度也很大,需要准确找到与xi分布相关的zi,需要大量的采样,因此需要在encoder中引入后验分布p’(z|xi),让xi与zi关联起来
(4)利用encoder通过假设已知数据的分布,拟合其参数,从而逼近真实的后验分布p’(z|xi),在这里假设后验分布是基于多元高斯分布,则让encoder输出分布的均值和方差
(5)总体流程
相关资料:https://zhuanlan.zhihu.com/p/348498294
3、Diffusion扩散模型
前向过程:
结论:任意时刻的分布都可以通过X0初始状态,以及步数计算出来。
Xt时刻的分布等于t-1时刻的分布+随机高斯分布的噪音,其中α是噪音的衰减值
同理t-1时刻的分布
带入到Xt公式
化简得到
最终得到任意步T的分布可由X0初始状态得到
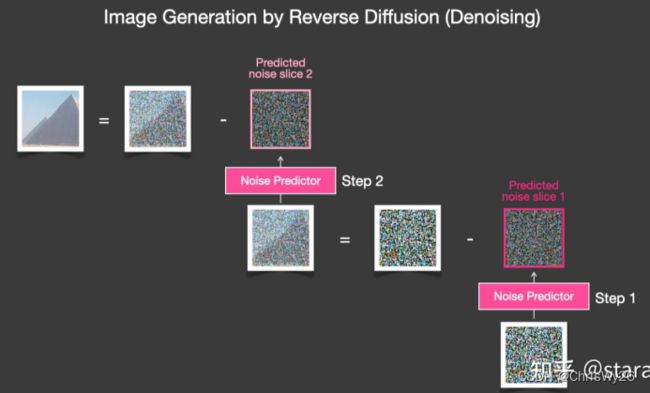
逆向过程:
已知Xt,求初始状态的X0,这里利用贝叶斯公式来预测X0
首先求一步,也就是已知Xt的分布求Xt-1时刻的分布,根据贝叶斯公式可得:
根据上面正向过程的公式,左式可求已知Xt-1时Xt的状态:
右侧分子分母在已知x0的状态,同样可以求出:
前向过程,也就是加噪的过程可以看做是不断构建标注的过程,在逆向过程中计算出去除噪音的分布,与前向过程中加的噪音计算损失
详细公式推导资料:由浅入深了解Diffusion Model - 知乎
4、多模态条件机制
Cross Attention:
(1)在transfomer中混入不同模态的两个序列,比如(图像、文本、声音)
(2)两个序列的维度必须相同
在stable diffusion的应用
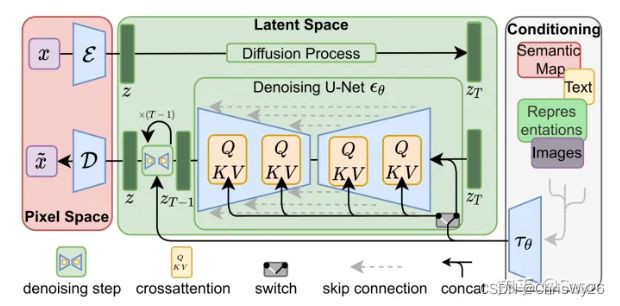
通过在Unet中间层引入cross attention,引入多模态的条件(文本,类别,layout,mask),其中cross attention的实现如下,其中Q来自latent space,K、V来自文本等另一序列:
5、Stable Diffusion原理
训练过程:
(1)使用预训练的CLIP模型,对需要训练的图像数据生成对应的描述词语。
(2)使用预训练的通用VAE或自己训练的VAE模型。通过VAE模型,先用Encoder部分对原图片进行处理,将输入图片信息降维到latent space,通常的降采样倍数在4-16倍之间效果最好。在sd中应用到AutoEncoderKL 的VAE模型将图像压缩到latent space。
(3)将压缩后的数据输入diffusion model,先进行正向采样,既通过输入的原始信息,一步一步生成噪声信息,在这个过程中,通过一个权重参数控制每步生成噪声的强度,越往后的step生成的噪声更多,直到生成纯噪声,并记录每步生成噪声的数据,作为GT
(4)利用cross attention将latent space的特征与另一模态序列的特征融合,并添加到diffusion model的逆向过程,通过Unet逆向预测每一步需要减少的噪音,通过GT噪音与预测噪音的损失函数计算梯度。
(5)其中Denoising Unet的结构如下:
前向过程:
- 根据假定分布,一般是多元高斯分布,生成一张纯噪音图像
- 利用VAE encoder 压缩到latent space
- 执行Denoising Unet,利用cross attention融合多模态信息
- 预测每一步需要减去的噪音,直到step执行完毕
- 利用VAE decoder还原到同一分布下的原图大小
Finetune 自己的模型:
- embedding:通过finetune clip text embedding 来补充词条与对应特征
- Hypernetworks: 通过超网络来加速模型训练