CNN基础论文 精读+复现----VGG(一)

前言

原文Github地址:https://github.com/shitbro6/paper/blob/main/VGG.pdf

原文arxiv地址 :https://arxiv.org/pdf/1409.1556.pdf

这篇文章一共14页，网络模型 是上一篇文章 AlexNet的进阶版。
在复现这篇文章之前，建议看一下Alex的精读文章
CNN基础论文 精读+复现----AlexNet(一)

第1页

摘要和引言主要是介绍了一下当下的历史背景和这个VGG网络。

VGG网络是牛津大学提出的，在当年的比赛ILSVRC2014中获得了定位项目第一名，分类第二名(第一名是GoogleNet)。

这里的提出了两个小概念:

• Localization(目标定位): 简单来说就是，识别的东西在哪里，是什么，指单一目标:

• Detection(目标检测): 简单来说 就是在哪里？分别是什么? 这里是指多目标:

摘要中说了一下大概的结构 对比之下将网络层推深到16-19层是最好的，也就是后面常说的 VGG16和VGG19，顺带提了一下，VGG使用了很多非常小的卷积核(3 x 3)，然后还说这个模型的泛化能力很好，放到其他的数据集上也有很好的表现，可以做迁移学习。

引言部分说到VGG的思想就是使用了更小的卷积核和更小的第一卷层步长，对图像的多个尺度上进行密集的训练和测试(先有个印象，后面会说)，还说明了本文解决了ConvNet的深度问题，提出了他们自己的 ConvNet。

第2-3页

第2，3页就开始介绍他们提出的更厉害的 ConvNet 了。

这俩页的几个关键点:

• 3 * 3卷积核: 为什么要使用 3 x 3 呢，论文中说是能捕捉周围视野的最小尺寸，想象了一下围棋棋盘，对于一个中心棋子，他的视野是其周围棋子就是上/下/左/右/左上/左下/右上/右下的位置。

  作者提到用两个 3 * 3 卷积核叠加代替一个 5 * 5 的卷积核。

  像下图这样：
  两个3 * 3卷积核得到一个值，直接用一个5 * 5 卷积也是一样得到一个值。
  

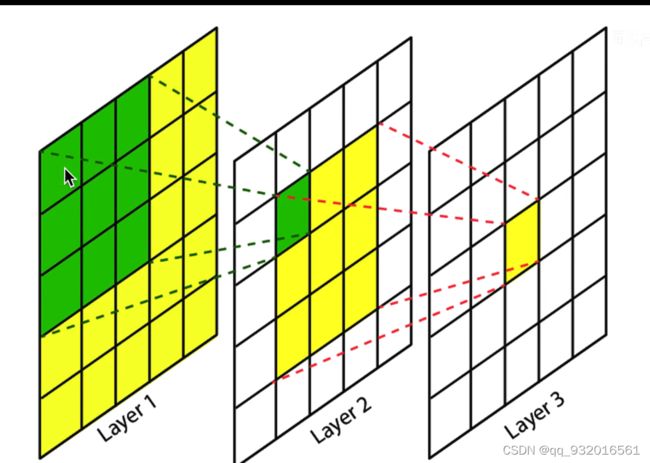
  同理3个 3 * 3的卷积核叠加可以代替一个 7 * 7 的卷积。这样做的好处是能将网络做的更深了，计算量更小了，增加了泛化能力和非线性能力。

  文章在2.3节做 3个 3 * 3 和1个 7 * 7的数量级对比，分别是 $27C^2$ 和 $49C^2$ ， 然后他说 前者比后者强81%？？我不理解，这是怎么算的 27比49强了81%吗？？ 不会是为了发文章搞的噱头吧?哈哈。

• 1 * 1卷积核： 就像下面这张图，若只有 1个小方块的卷积核，显然他在扫描的时候是没有办法看到当前扫描方块的周围情况的，所以 1 * 1卷积核没有办法识别空间位置信息，但可以融合通道信息。
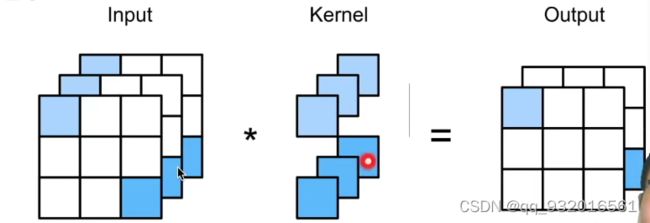
  使用1 * 1 卷积核可以使网络深度增加，增加非线性能力，也可以达到升降维度的作用（本论文中没有体现这个作用）。

• VGG block : 对应原文中的话是 A stack of convolutional layers 简单理解就是VGG块。将之前alex里的若干个层放到一起形成VGG块，VGG网络就是一堆VGG块组合而成(再加线性层),知乎上找了张图便于理解:

• regularisation（正则化）: 2.2里提到的一个概念，通俗的讲，所有能降低过拟合的方法，都可以叫做正则化，比如VGG把模型变深，或者在alex里的dropout。

下面这张论文第三页的这个图简单解释一下:

竖着每一组都是一个对照实验组。

A组 11层(8卷积+3全连接，只算带权重的层 所以池化层不算)。

另一个A组加上LRN。

还有B C D E组。

D,E组就是平常说的VGG16和VGG19。

而C和D都是 16层， 他俩的区别是 C组使用了1 * 1卷积核，而D组都是3 * 3 卷积核。

图中加粗的就是增加的或者修改的层。

这里面是有Relu的 只是他没写出来。

这里的每一个方块就是上面说的VGG块，比如D组第二个块 里面的两个conv3-64 ，就说明当前VGG块里有两层 64个卷积核(也就是生成64个通道) 的 3 * 3的卷积层。可以不断加VGG块数，就是增加了深度增加了通道数(不断提取图片特征)，减小了图片尺寸。

每一个VGG块后都接最大池化层，最后是三层线性层+softmax收尾。

后面这个图表达每个模型的参数量，单位是百万。

可以看到 VGG16有 1亿3千8百万的数量级。非常多啊~~

然后作者还不忘自恋一波夸赞一下自己的网络，说自己的网络虽然很深但是权重参数数量对比更大的卷积宽度和感受野的较浅网络中更少，这里原文说到144M weights in (Sermanet et al., 2014) 比2014年的 overfeat的权重更小。你家的E实验组不也是144M的数量级吗，而且咋不和googleNet比呢(googleNet 数量级5.9M)，哈哈 这就无语呀~

在这里就可以发现 VGG的一个重要缺陷就是数据量比较大。

第二章的最后还诋毁了一下其他的论文结构模型哈哈，作者666。

第四页

第4页开始介绍一些训练和评估的细节，训练整体和Alexnet基本一致，只有细微差别，也是使用mini-batch随机梯度下降、反向传播同时也包含dropout 和权重衰减等，然后说了一些具体的设置参数，像batch size 动量啊 这些后面用代码构建网络模型的时候再细说把。

后面说了一下初始权重设置的重要性，和数据增强方法，就是跟前面的Alexnet差不多，就是随机的水平翻转和随机RGB颜色偏移。

为了获得固定大小的224×224 ConvNet输入图像，从归一化的训练图像中随机裁剪。令S是等轴归一化的训练图像的最小边(宽高等比例缩放)后的图片的最小边长，ConvNet输入从S中裁剪（我们也将S称为训练尺度）。考虑两种方法来设置训练尺度S，一种方法是固定S的大小，另一种方法是从一定区间内随机取S。

举个例子，这里设training scale S = 224。有三幅经缩放后的图片：A,B,C。尺寸长×宽分别为：A 200×400,B 224×600 C 600×900 则A的最小边200<224,不可以进行裁剪；B、C可以（且对B的任何裁剪范围，都只能在宽600所在的边上移动）

第五页

第5页这里3.2小节就是介绍测试的细节了，用密集的训练方式进行测试，把所有的全连接层都变成了卷积层，也就是此时的网络是全卷积网络，所以可以输入各种不同尺度的图像，如果输入的是224 就是前面定义过的244尺寸，则这个网络结构就等价于原来的带全连接层的网络，如果输入的大于244(3.2节开头将这个值设置为Q了)，则整个网络就是全卷积网络，最后输出的时候就是就不是一个向量了，应该变成4D张量了，再通过一个全局平均池化层变成了一个向量，之后再翻转了图片，又得到了一个结果，最终结果取两者的平均值。

看到这里我有点懵，没怎么懂是如何全连接变成卷积层的，这里引用一下同济子豪兄的笔记:

改造之前:

假如网络是这样的 N个卷积 -> 全连接 -> 全连接 像下图这样:

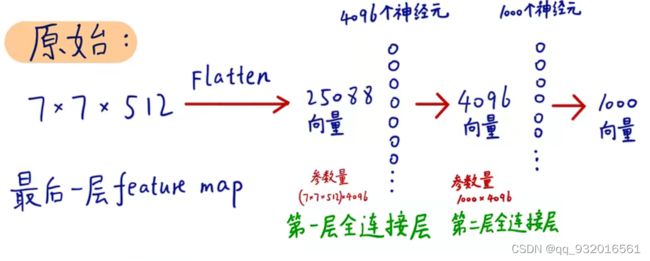
假如N个卷积之后的数据变成 7 * 7 * 512 则此时展成向量 变成 25088个元素的向量，通过一个4096神经元的全连接层 ，变成4096个元素的向量，再通过一个1000个神经元的全连接，最后输出1000个元素的向量。

改造之后:

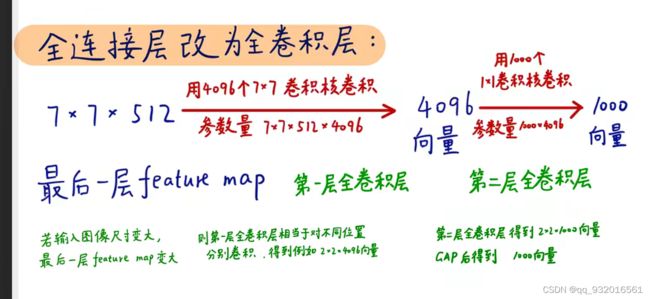
当得到前面的数据 7 * 7 * 512之后，不将其展开成向量，而是直接送去有 4096 个 7 * 7卷积核的卷积层，对比改造之前看，其实就是将改造之前的全连接层里的4096个单神经元变成了 7 * 7的卷积核，参数依旧是等量的。同理，后面就变成了1000个 1 * 1卷积核的卷积层(实际上论文中是三层全连接层，改一个7 * 7 卷积层 和 两个 1 * 1 卷积层，他这里少画了一层 1 * 1的卷积层）。

所以也就明白了为什么说改造成全卷积之后可以接受任何尺度的变换，因为改造之前的全连接层4096神经元是固定的，而改造之后的全卷积网络，输入变换之后只要滑动扫描几次就行了。

他这种改造成全卷积网络然后输入各种的大尺寸图像的方法就是前面说到的密集型训练方法。

3.3小节说了一下实现代码用到的工具，框架用的 C++写的Caffe，然后对这个框架进行改造让他能跑多个GPU(数据并行)，就是将 一个batch分成四份给 4个GPU，让4块GPU算完后再汇总。

整篇文章前半部分到这就差不多了，第六页 也就是第四章开始介绍模型性能了，所以后面我就先把模型代码复现出来，然后继续看论文。。。。。。。。。。。。。。

后续 ：CNN基础论文 精读+复现----VGG(二)