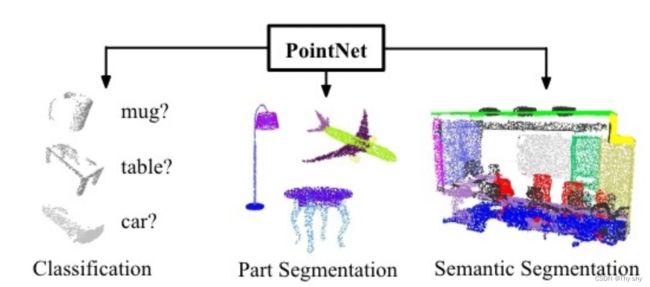
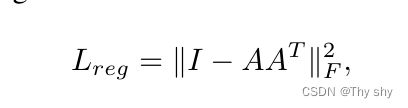PointNet论文分析
PointNet: Deep Learning on Point Sets for 3D Classification and Segmentation
一.摘要
本文提出了一种直接计算点云的新型神经网络,可以处理输入点点排列不变性。该神经网络名为PointNet,为对象分类、部分分割和语义分割提供了统一的框架。PointNet简单、高效且有效。可以实现新的sota。本文还从理论上分析了网络学到了什么,以及网络为什么具有鲁棒性。
本文的主要贡献:
- 设计了一种应对无序的点云的神经网络架构
- 展示了如何训练网络执行分类、部分分割和语义分割任务
- 对该方法对稳定性和效率进行了全面的实证和理论分析
- 说明了网络中所选神经元计算的3D特征,并对其性能进行了直观的解释
二.相关工作
Point Cloud Features
大部分现有的点云功能都是针对特定任务手工制作的。点的特征通常对点的某些统计属性进行编码,并设计为对某些转换保持不变,这些转换通常被分类为内在的或外在的。也可以分为局部特征和全局特征。对特定任务找到最优特征组合并非易事。
Deep Learning on 3D Data
3D数据有多种表示形式,导致了各种学习的方法。其中有Volumetric CNNs、FPNN、Vote3D、Spectral CNNs、Feature-based DNNs等等。
Deep Learning on Unordered Sets
从数据结构的角度来看,点云是一组无序的向量,点云在深度学习方面并没有做太多工作。
三.点云的特性
- 无序性
与图像和自然语言不通,点云是一组没有特定顺序的点,换句话说,一个输入为N个点的网络需要对N!种排列顺序的输入保持等价的输出
- 点之间相互作用
这些点来自具有距离度量的空间,这意味着点与点并不是孤立的,相邻的点形成一个有意义的子集。所以模型需要能够从附近的点捕捉局部结构,已经局部结构之间的组合相互作用。
- 变换不变性
作为一个几何对象,点集的学习表示应该对某些变换是不变的。不如说,一个飞机的点集无论怎么旋转平移,都不应该影响它的分类和分割。
四.PointNet架构
以上是PointNet的全部架构。点云的三个特性已经介绍,下面就解释该网络架构如何解决这三个问题。
1.使用对称函数处理无序性
为了让模型对输入顺序保持不变,存在三种策略:
1. 将输入排序为规范顺序
2. 将输入视为一个序列来训练RNN,但通过各种排列来扩充训练数据
3. 使用一个简单的对称函数来聚合来自每个点的信息
对于第三点,介绍一下对称函数,可以说对全局变量进行处理和满足交换率的数学计算,都可以是对称函数,比如说求均值,求最大值,或加法,或乘法。
尽管排序听起来是一个简单的方案,但是在高维空间中实际上不存在稳定的排序,这点论文进行了理论和实验的论证。
RNN对小长度的序列的输入排序具有较好的鲁棒性,但是很难扩展到数千个输入元素,这是点集的常见大小。根据实验也不如我们提出的方法。
论文的想法是通过对几何中的变换元素应用对称函数来近似定义在点集上的一般函数:
基本模块是非常简单的,通过MLP逼近h,通过单个变量函数和最大赤化函数的组合来逼近g。通过实验发现这很有效。
架构中有一个细节:
可以看到MLP参数都是共享的,可以想象一下,输入不同的顺序,经过相同的MLP得到一个n✖️1024的矩阵,再在n这个维度取最大值,无论输入的是什么顺序,得到的都是一个1✖️1024的全局特征。这就解决了处理无序性的问题。升维到1024的特征值也足够进行分类了。
2.局部和全局信息联合
上述部分得到的全局向量,可以轻松利用MLP进行分类。然而点的分割需要结合局部和全局的信息,可以通过一种简单而高效的方式实现。
可以看到架构把全局信息和局部点的信息拼接在了一起,这样就解决了局部信息和全局信息联合的问题。
3.加入Alignment Network解决变换不变性
我们希望我们的点学习到的表示对刚性变换这些转换是不变的。
如果学过spatial transformer就发现这很类似,spatial transformer可以旋转平移2D图像,而在这里使用T-Net学习一个矩阵,与点集相乘后就可以将点集变换到loss最小的三维空间。
这个想法可以拓展到特征空间的对齐,但是特征空间中的变换矩阵比空间变换的矩阵维数高的多,大大增加了优化的难度,因此增加了一个正则化项,尽量让特征变换矩阵接近正交矩阵。
至于为什么要正交矩阵,可以去查正交矩阵的性质。
五.理论分析
这段数学式大概在说,f在s的豪斯多夫距离上是连续的,只要有足够的神经元,网络可以任意逼近f,至于推导我也不懂。
这个定理的证明在论文的补充材料里有。关键思想是,在最坏的情况下,网络可以通过将空间划分为相等大小的体素来学习将点云转换为体积表示。
下面是一个很有用的数学公式,介绍了瓶颈维度和稳定性。
仔细看(a)公式,存在一个Cs,f(T)=f(S),然而T只是全局的一个子集,它只要包含Cs网络的表示就不会出问题,这就说明只要Cs中的点都被保留了,那你损坏多少点都不会影响结果。噪声点达到Ns它也不回变化。
(b)公式表示,f(S)实际上完全与小于等于K个元素的有限子集Cs确定。因此将Cs称为S的临界点集,将K称为f点瓶颈维度。
这就解释了模型对扰动点、损坏和额外噪声点的鲁棒性。直观的说,网络通过一组稀疏的关键点来学习总结一个形状。
该图中间的部分就是临界点集,下部分是上限点集,落在这两个点集之间的点云都会给出完全相同的特征。
六.总结
提出了PointNet这种新型深度神经网络,为3D识别任务提供了统一的方法。还提供了理论分析和可视化,以了解这个网络。