Gurobi处理非线性目标函数和约束的详细案例
Gurobi处理非线性目标函数和约束的详细案例
- 非线性项举例
- `Quadratic Programming`
- `Quadratically Constrained Programming`
- `Quadratically Constrained Quadratic Programming`
- `Second-Order Cone Programming`
- 其他Gurobi可以求解的非线性形式
- Gurobi代码实现
-
- 一些闲言
- 简单讲解
- 完整模型构建
- 注意事项
- 参考文献
作者:刘兴禄,清华大学,清华伯克利深圳学院博士在读
文中的图片(除聊天截图外)均来自作者待出版的教材《运筹优化常用算法、模型及案例实战:Python+Java 实现》
非线性项举例
在运筹优化中,我们经常会遇到一些非线性的问题,主要包括
- 非线性目标函数
- 非线性约束
这两者也可以只有其一,也可以兼而有之。一般,Gurobi可以求解的非线性问题为下面几类:
- 目标二次,约束一次(
Quadratic Programming,QP) - 目标一次,约束二次(
Quadratically Constrained Programming,QCP) - 目标二次,约束二次(
Quadratically Constrained Quadratic Programming,QCQP) - 目标一次,约束是锥约束(
Second-Order Cone Programming,SOCP)
如果上述模型中有整数变量,则相应的模型就变为MIQP, MIQCP, MIQCQP, MISOCP。
下面举几个这种模型的例子。
Quadratic Programming
max x 2 + y 2 + z 2 x + y ⩽ 5 x + z ⩽ 6 x , y , z ⩾ 0 \begin{aligned} \max \quad &x^2 + y^2 + z^2\\ &x+y\leqslant 5\\ &x+z \leqslant 6\\ & x, y, z \geqslant 0 \end{aligned} maxx2+y2+z2x+y⩽5x+z⩽6x,y,z⩾0
如果上述模型中, x ∈ Z x\in \mathbb{Z} x∈Z,这就是一个MIQP.
Quadratically Constrained Programming
max x + y x 2 + y 2 ⩽ 5 x , y ⩾ 0 \begin{aligned} \max \quad &x + y\\ &x^2 + y^2\leqslant 5\\ & x, y\geqslant 0 \end{aligned} maxx+yx2+y2⩽5x,y⩾0
如果上述模型中, x ∈ Z x\in \mathbb{Z} x∈Z,这就是一个MIQCP.
Quadratically Constrained Quadratic Programming
max x 2 + y 2 2 x 2 + 3 y 2 ⩽ 5 x , y ⩾ 0 \begin{aligned} \max \quad &x^2 + y^2\\ &2x^2 + 3y^2\leqslant 5\\ & x, y\geqslant 0 \end{aligned} maxx2+y22x2+3y2⩽5x,y⩾0
如果上述模型中, x ∈ Z x\in \mathbb{Z} x∈Z,这就是一个MIQCQP.
Second-Order Cone Programming
max x + y + z 2 x 2 + 3 y 2 ⩽ 3 z + 5 x 2 + y 2 ⩽ z 2 x , y , z ⩾ 0 \begin{aligned} \max \quad &x + y + z\\ &\sqrt{2x^2 + 3y^2}\leqslant 3z+5\\ &x^2 + y^2 \leqslant z^2\\ & x, y,z\geqslant 0 \end{aligned} maxx+y+z2x2+3y2⩽3z+5x2+y2⩽z2x,y,z⩾0
如果上述模型中, x ∈ Z x\in \mathbb{Z} x∈Z,这就是一个MISOCP.
加上基本的MIP,一共5类,这是Gurobi可以求解的5类常见的问题。通常情况下,用户的需求,都是带整数变量的。除了以上5类,Gurobi还可以求解很多其他类型的非线性问题。
其他Gurobi可以求解的非线性形式
Gurobi代码实现
一些闲言
上面非常简略的介绍了一些非线性的知识。接下来我们进行实操。

是吧,这问题其实在很多个地方,已经回答过几十遍了,我觉得还是出一个推文比较好。
简单讲解
下面我们来看一个最简单的形式。假设我们想要使用Gurobi构造一个非线性表达式
x 2 + y z \begin{aligned} x^2 + yz \end{aligned} x2+yz
该怎么做呢?首先,我们需要构造一个二次表达式对象,然后通过在二次表达式对象中添加项的方式,完成表达式的构建。
具体代码如下(我们直接展示完整的代码)
# 建立模型对象
model = Model("MyModel")
# 构建变量
x = model.addVar(lb = 0, vtype=GRB.CONTINUOUS, name="x")
y = model.addVar(lb = 0, vtype=GRB.CONTINUOUS, name="y")
z = model.addVar(lb = 0, vtype=GRB.CONTINUOUS, name="z")
# 建立二次表达式
quadExpr = QuadExpr()
# 添加项:addTerms()
quadExpr.addTerms(1, x, x) # 添加项x * x
quadExpr.addTerms(1, y, z) # 添加项y * z
这样就完成了费此案性表达式的构建。
完整模型构建
max x 2 + y z x y + y z ⩽ z + 5 x + z ⩽ 6 x ∈ Z + , y , z ⩾ 0 \begin{aligned} \max \quad &x^2 + yz\\ &xy + yz \leqslant z + 5\\ &x+z \leqslant 6\\ & x \in \mathbb{Z}+, y, z \geqslant 0 \end{aligned} maxx2+yzxy+yz⩽z+5x+z⩽6x∈Z+,y,z⩾0
代码如下
from gurobipy import *
# 建立模型对象
model = Model("MyModel")
# 构建变量
x = model.addVar(lb = 0, vtype=GRB.INTEGER, name="x")
y = model.addVar(lb = 0, vtype=GRB.CONTINUOUS, name="y")
z = model.addVar(lb = 0, vtype=GRB.CONTINUOUS, name="z")
model.setObjective(x * x + y * z)
# 建立二次表达式
quadExpr = QuadExpr()
# 添加项:addTerms()
quadExpr.addTerms(1, x, y) # 添加项x * x
quadExpr.addTerms(1, y, z) # 添加项y * z
model.addQConstr(quadExpr <= z + 5)
model.addConstr(x + z <= 6)
model.optimize()
运行结果如下
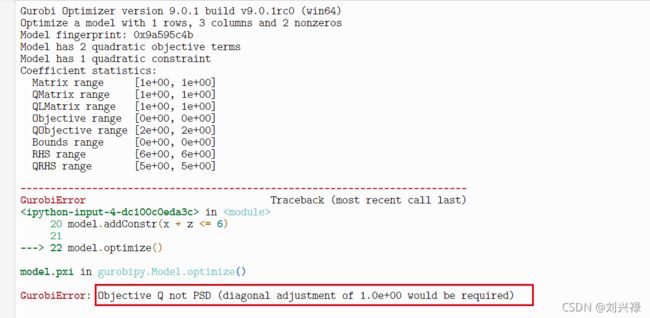
提示说,目标函数不是PSD的,也就是不是Positive semi-definite (PSD)(整半定)。所以这种非线性的如果要能求解,就必须需要目标函数是PSD的才可以(小伙伴们可以对目标函数的表达式进行求导验证,确实不是PSD的),我们更改目标函数为
max x 2 + y 2 x y + y z ⩽ z + 5 x + z ⩽ 6 x ∈ Z + , y , z ⩾ 0 \begin{aligned} \max \quad &x^2 + y^2\\ &xy + yz \leqslant z + 5\\ &x+z \leqslant 6\\ & x \in \mathbb{Z}+, y, z \geqslant 0 \end{aligned} maxx2+y2xy+yz⩽z+5x+z⩽6x∈Z+,y,z⩾0
并在代码中进行修改,如下
model.setObjective(x * x + y * y)
结果如下
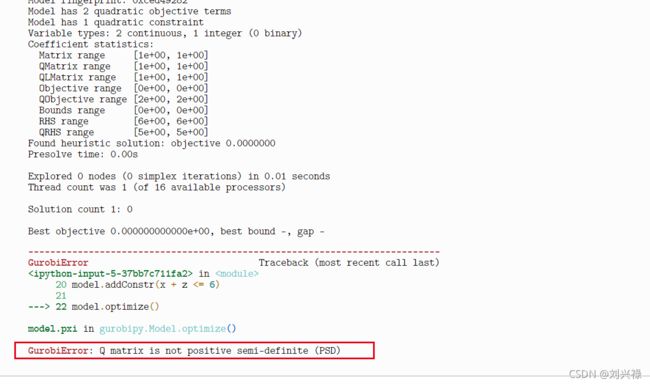
这里又说,约束矩阵中,二次的部分 Q Q Q不是PSD的,确实,小伙伴们可以对约束的表达式进行求导验证,确实,约束也不是PSD的。
综上,一个非线性的(二次)的模型,在Gurobi中可以被求解,前提就是目标函数和约束,都需要是PSD的,这样Gurobi才可以求。我们试试下面的二次模型。
max x 2 + y z x 2 + x y + y z ⩽ z + 5 3 x + 2 z ⩽ 4 x , y , z ∈ { 0 , 1 } \begin{aligned} \max \quad &x^2 + yz\\ &x^2 + xy + yz \leqslant z + 5\\ &3x+2z \leqslant 4\\ & x,y,z \in \{0,1\} \end{aligned} maxx2+yzx2+xy+yz⩽z+53x+2z⩽4x,y,z∈{0,1}
from gurobipy import *
# 建立模型对象
model = Model("MyModel")
# 构建变量
x = model.addVar(lb = 0, vtype=GRB.BINARY, name="x") # INTEGER
y = model.addVar(lb = 0, vtype=GRB.BINARY, name="y")
z = model.addVar(lb = 0, vtype=GRB.BINARY, name="z")
model.setObjective(x * x + y * z, GRB.MAXIMIZE)
# 建立二次表达式
quadExpr = QuadExpr()
# 添加项:addTerms()
quadExpr.addTerms(1, x, x) # 添加项x * x
quadExpr.addTerms(1, x, y) # 添加项x * x
quadExpr.addTerms(1, y, z) # 添加项y * z
model.addQConstr(quadExpr <= z + 5)
model.addConstr(3 * x + 2 * z <= 4)
model.optimize()
print('x = ', x.x)
print('x = ', y.x)
print('x = ', z.x)
求解结果如下。

经过探索,上面的模型,我们把 x , y , z x,y,z x,y,z改成BINARY的变量,就是可以求解的,但是如果改成CONTINUOUS和INTEGER的,就是不可以求解的。
如果把所有的二次项 x 2 , x y , y z x^2, xy, yz x2,xy,yz的取值,都控制成 { 0 , 1 } \{0,1\} {0,1},这样就是一定可以求解的,这样,就只能是3个变量都是BINARY的。
注意事项
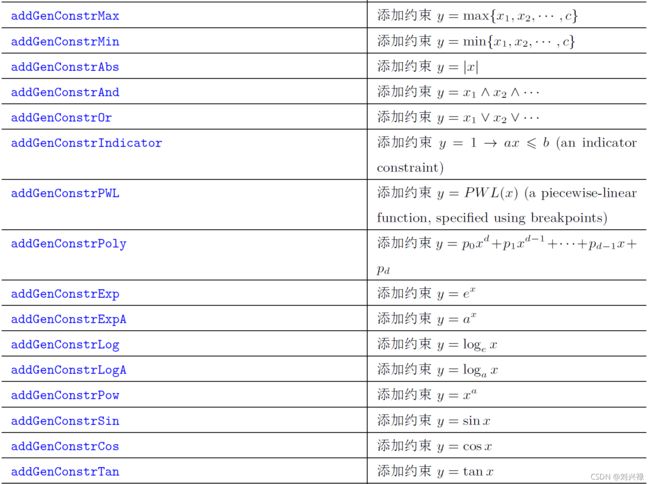
关于其他高次方或者指数形式的约束和表达式(如下图),Gurobi是可以处理的,但是,都是一些近似,不能保证就是最优解。这一点大家一定注意,Gurobi是对这些函数进行了线性逼近,是一种近似的处理,不一定就是最优解。
好了,今天的分享就到这里,之后有机会再做更加详细的介绍。
参考文献
[1]. 运筹优化常用算法、模型及案例实战:Python+Java 实现. 刘兴禄,熊望祺,臧永森,段宏达,曾文佳,陈伟坚(待出版).
[2]. Gurobi Optimizer Reference Manual.
作者:刘兴禄,清华大学,清华伯克利深圳学院博士在读