Pointnet 论文解读精讲
文章目录
- 摘要(abstract)
- 介绍(Introduction)
- 相关工作(related work)
- 问题陈述(Problem Statement)
- Deep learning on point Sets
-
- Properties of point Set
- PointNet Architecture
-
- Symmetry Function for Unordered Input
- Local and Global Information Aggregation
- Joint Alignment Network
- Analysis and Result
原文:https://arxiv.org/abs/1612.00593
git:https://github.com/charlesq34/pointnet
摘要(abstract)
原文概述。点云是一个很重要的几何数据形式。但由于他具有无序性(irregular format),所有大部分算法在处理点云时,都将点云变换到顺序的3D 体素(3D voxel)或者投影成图片形式等。但这样一般会导致输入数据变得的稀疏,会产生其他问题。所以在本篇论文中,我们提出了一个算法叫PointNet用来直接对点云进行操作,使用一个神经网络对点云进行语义分割,分类,部分分割等操作。而且本算法还用到置换不变性。以及表述了他在当时最棒的情况(哪篇论文不是,屁话。)
介绍(Introduction)
典型的卷积结构都需要高度规则(顺序化)的数据作为输入,比如3D voxels 或者 图片。这样可以保证参数的共享和一些其他kernel optimization等。但点云不是这样的结构,所以大部分其他算法都会将其转化为3D voxel或者投射成image(BEV)等形式进行后续操作。
缺点:这样的方式会造成有很多不必要的体积划分使得输入数据变得稀疏,同时会影响点云数据的不变性。

PointNet从不同的角度出发来解决这一问题,考虑到点云数据的本质是一个点集,它具有一下特征:
- 无序性,点云是一个点集,没有固定的顺序;
- 与邻域点又相互作用,点云中的个体不是独立的,与周围的点具相关,具有局域特征;
- 刚体旋转、平移不变性,旋转和平移不会改变点云的分类、分割结果。
针对上三个特性,设计了如下的网络解决问题。
前两点解释:
所以我们就聚焦于直接将3D点云数据送入网络进行操作的方法。此方法命名为PointNets。这个网络结构简单统一,同时还避免了组合的不规则性以及复杂性,所以就会更容易去训练。同时我们还考虑到点云具有排列不变性(无序性),以及对对称函数的不变性。(简单来说maxpooling/averagepooling等)。
此网络将点云直接输入,输出可以根据不同任务进行调整,分类的话,输出类别,语义分割的话,每个点的类别就可以了。过程中要强调,一直到最后的global feature前,网络都是对每一个点单独操作,并且权重共享的。当然输入可以是(x,y,z)等坐标信息,也可以加入法向量呀,rgb呀等局部或者全局特征,都可以的。
对此算法来讲一个重要的点是,在取得全局特征时,我们利用了对称函数:max pooling 。这保证了即使是无序的特征点,最后输出的却是确定的特征。很简单么,无论你怎么排序,max pooling不变呀,所以顺序性对max pooling之后的特征不影响,所以这个网络就可以实现。
当然这个过程也可以这样理解,每一次的mlp操作,都是对点云的一次筛选,最终留下了对后续任务有用的点。可视化出来,就像用多少点能表示这个物体一样,我们把这些点找到就可以了。所以这也是算法对干扰呀,缺失呀,outliers比较robust的原因。然后全连接层将这些信息聚合起来,满足了相关任务的需求。
最后一点
又因为我们在max pooling前,网络都是对单独的点进行操作,所以我们可以对其进行变换,(也因为点云的旋转不变性,但仅仅对分类适用,如果是点云恢复之类的任务就不行了哈。)这样就能在网络操作前,统一规范数据,也就能一定程度上提高网络结果。和BN有点相同的意思吧。作用是:不依赖于数据的空间变化网络来处理刚体或仿射变换,在输入网络前对点云数据进行规范化(canonicalize)处理, 消除旋转等变换带来的影响。
再后边就是将通过实验,他是最好的事情了。
列举下算法的贡献:
- 我们设计了一个新颖的深层网络架构来处理三维中的无序点集
- 我们设计的网络表征可以做三维图形分类、图形的局部分割以及场景的语义分割等任务
- 我们提供了完备的经验和理论分析来证明PointNet的稳定和高效。
- 充分的消融实验,证明网络各个部分对于表征的有效性。
相关工作(related work)
- Point Cloud Features
- Deep learning on 3D data
- Deep Learning on Unordered Sets
因为这篇文章真的有点早,所以这个相关工作不看也罢,现在都飞速发展了,最简单的pointnet++,都比这个好啦~所以不赘述啦。
问题陈述(Problem Statement)
简单说下问题的输入输出。输入是3D点云集合,根据不同人物从完整的3D点云处理后的分割部分。比如分类的话,从预分割的点云集合中的一个场景的点云,作为输入,输出是k个类别的score。分割的话,就是一个固定场景或者一个预分割的后的物体,输出是每个点的类别score * 点数。
Deep learning on point Sets
Properties of point Set
实际介绍的时候都讲了,再罗列一遍吧。
- 无序性,点云是一个点集,没有固定的顺序;相应的那网络就要对点云的排序要invariant。
- 与邻域点又相互作用,点云中的个体不是独立的,与周围的点具相关,具有局域特征;相应的网络就要能得到局部的特征并且得到相关的组合以及最后的全局特征。
- 刚体旋转、平移不变性,旋转和平移不会改变点云的分类、分割结果。这个好理解啦,刚体的旋转平移不影响分类结果。
PointNet Architecture
- max pooling 模块用来聚合全部点的信息。
- 局部和全局的信息结合模块
- two joint alignment networks that align both input points and point features.
Symmetry Function for Unordered Input
这里是为了解决输入数据的无序性问题。那么正常方法的话,如何去解决呢?三种常见方法:
- 给无序的数据按照一定要求排序(3D voxel or BEV,问题:不稳定,或者很难找到稳定的方法)
- 用RNN进行训练,同时在数据增强时,使用所有的顺序。(点云数据太大了,RNN也很难去拟合)
- 使用一些对称的结构去聚合信息。(简单来说,就是对数据的顺序具有invariant)比如加法,乘法,都具有交换律。在DL领域,各种pooling不就有这种属性。
后边就讲了前两种方法不太行,有各种缺陷和问题。所以此算法选择了第三种方法,使用了maxpooling函数解决这个问题。
Local and Global Information Aggregation
从maxpooling出来的全局特征接一个FC层就可以直接得到类别信息。但是如果是做分割任务,则还需要局部和全局特征的融合。
这里的实现方式也很简单高效。如上图所示,我们将得到的全局vector和之前每个点的local vector分别进行拼接。这样就得到了对每一个点来说,既有local又有global的feature。所以就可以用于后续的分割任务。
后边还讲了这个方法结果非常好,就不赘述了。
Joint Alignment Network
这里实际就是讲的上图中的T-Net,主要是解决刚体的旋转不变性、平移不变性的问题。
常规方法是在输入数据前,将其按照一定规则变换到一个固定的形态。可以这么做,但麻烦且复杂。所以此算法用了一个简单的方法,达到了相同的效果。
此算法在数据特征提取的过程中,加入了一个affine transformation matrix,而且这个变换和整个网络一样,是可以学习的,又因为变换是对每一个点进行操作,所以不影响之前所说的所有特性。从而得到的结果就是将所有的数据对在一定维度上进行了对其,解决了刚体的旋转不变性、平移不变性的问题。(文中说在补充材料中有更多的解释,但这篇论文只是用来看下基础,就不去深究了。而且后续似乎也没人用这个方法。)
Analysis and Result
PointNet通过上面的操作,可以得到一个稀疏的关键点集来描述总结点云所表示的形状:

上图中,第一行是原始数据、第二行树关键点集(类似于骨架)、第三行为外形的上边界。关键点集相当于定义了形状的全局特征,所有的点都将落在第二行和第三行表示之间。网络的鲁棒性就来源于此处,只要保留了关键点,及时点云有变换和扰动结果也不会受到影响。同时关键点集合也意味着可以描述整个点云的性质。
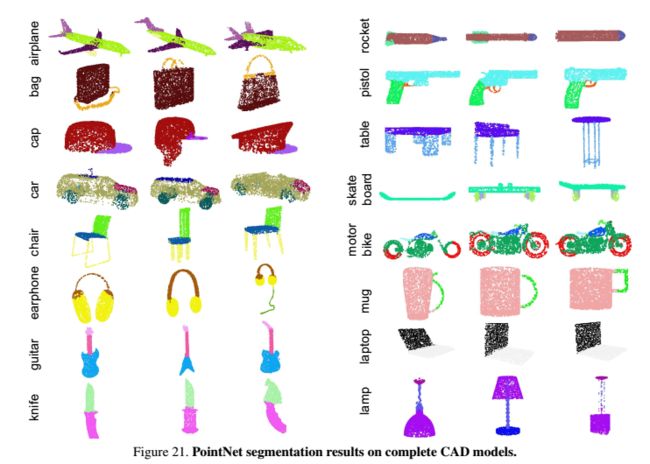
几个不错的结果:
不足:缺乏在不同尺度上提取局部信息的能力(因为基本上都是单点采样,代码底层用的是2Dconv,只有maxpooling整合了整体特征,所以局部特征提取能力较差)
PointNet之所以影响力巨大,并不仅仅是因为它是第一篇,更重要的是它的网络很简洁(简洁中蕴含了大量的工作来探寻出简洁这条路)却非常的work,这也就使得它能够成为一个工具,一个为点云表征的encoder工具,应用到更广阔的点云处理任务中。
未参考,但是觉得写得很好的解析:https://cloud.tencent.com/developer/article/1746489