pythonarma模型t检验_【描述时序】趋势、季节和随机性

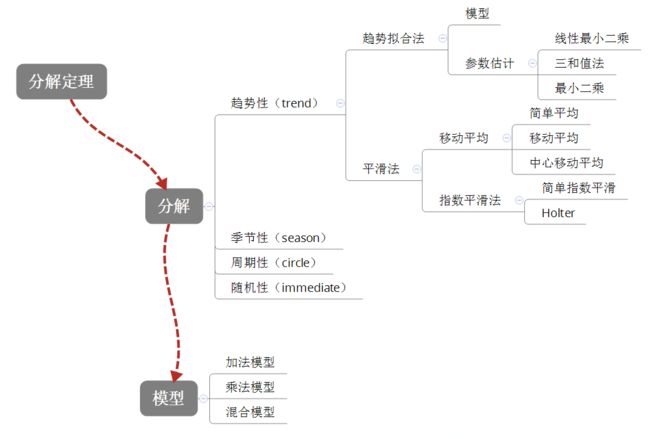
先看此知识体系：

1. 分解

1.1 分解定理

wold分解定理

(1938)

任何一个离散平稳过程$x_t$都可以分解为两个不相关的平稳序列之和，其中一个为确定性的，另一个为随机性的。

$x_t=V_t+\xi_t$

其中，

$V_t$是确定性序列

$\xi_t=\sum\limits_{j=0}^\infty \phi_j \varepsilon_{t-j}$是随机序列

$\phi_0=1,\sum_{j=0}^\infty \phi_j^2

$\varepsilon_t\sim N(0,\sigma_\varepsilon^2)$，也就是白噪声序列

$E(V_t,\varepsilon_s)=0,\forall t\neq s$

下面定义什么事 确定性序列 和 随机性序列

$y_t=a_0+a_1y_{t-q}+a_2y_{t-q-1}+…+v_t$

$v_t$是残差，定义$\tau_q^2=Var(v_t)$

如果$\lim\limits_{q\to\infty}\tau_q^2=0$，那么$y_t$叫做确定性序列

如果$\lim\limits_{q\to\infty}\tau_q^2=Var(y_t)$，那么$y_t$叫做随机性性序列

例如：

ARMA模型

$x_t=\mu+\dfrac{\Theta(B)}{\Phi(B)}\varepsilon_t$

首先是离散平稳过程，其次两部分分别是确定性序列、随机性序列。

Crammer分解定理

(1961)

任何一个时间序列( 不要求平稳)都可以分解成两部分的叠加：

一部分是由多项式决定的确定性趋势成分

另一部分是平稳的零均值误差成分，

$x=u_t+\varepsilon_t$

$u_t=\sum\limits_{j=0}^d\beta_jt^j$ 确定性影响

$\varepsilon_t=\Psi(B)a_t$ 随机性影响

1.2 分解模型

进行分解时，有以下一些方法。

结构性分解：需要其它经济变量，用变量之间的关系分离出趋势成分和循环成分，如Okun分解，Philllips曲线关系等

状态性分解：通过时间序列的性质，分解成趋势成分和循环成分

状态域分解：卡尔曼滤波，差分分解

频域分解：H-P滤波，BP滤波

这里只介绍最直观的分解方法。

一个时间序列，可以由以下因素组成：趋势性(Trend)，周期性(Circle)，季节性(Season)，随机性(Immediate)

每个性质的拟合方法是：

趋势性

趋势拟合法

平滑法

移动平均

指数平滑

季节性

周期性

随机性

具体模型有：

加法模型

$Y_t=T_t+S_t+I_t$

乘法模型

$Y_t=T_t S_t I_t$

混合模型

$Y_t=S_tT_t+T_t$

$Y_t=S_t(T_t+I_t)$

其它个性化定制的模型

如果季节的波动性与趋势没有关系，那么考虑加法模型。如果季节的波动性随着趋势性变化，那么考虑乘法模型。

下面分别介绍每一个性质的处理方法。

1.趋势性

1.1 趋势拟合法

常见的模型类型

罗列一下常见的模型类型

直线趋势模型

$\hat Y=a+bt$

二次曲线模型

$\hat Y=b_0 +b_1 t +b_2 t^2$

三次曲线模型

$\hat Y=b_0 +b_1 t +b_2 t^2+b_3 t^3$

幂函数曲线模型

$\hat Y=a t^b$

对数曲线模型

$\hat Y= a+b \ln b$

双曲线模型

$\hat Y= a+b \times \dfrac{1}{t}$

指数曲线模型

$\hat Y=ae^{bt}$

修正指数趋势模型。特点是有增长上限

$\hat Y=L+ae^{bt},a<0,b<0$

贡伯兹曲线。

$\hat Y=L e^{-ae^{-bt}},a>0,b>0$

特点：

$t \to - \infty \ni Y \to 0$

$t \to \infty \ni Y \to L$

曲线有拐点，先凹后凸

皮尔曲线模型

皮尔曲线又叫logistic曲线，较好的描述了生物生长的过程

$\hat Y= \dfrac{L}{1+ae^{-bt}}$

趋势模型的参数估计

《统计预测：方法与模型》给出了两种估计参数的方法：线性最小二乘法，三和值法。scipy给出了一种估计参数的方法：最小二乘估计。

线性最小二乘法

把模型变换成为线性模型，然后用OLS进行估计。

例如，贡伯兹模型，可以变换成$\ln \ln (L/Y)=\ln a -bt$

优点：可以使用线性回归的所有检验方法(t检验，F检验…)

缺点：

有些模型对应多个线性模型。

往往残差不是最小。(而是变换后的线性模型残差最小)

三和值法

把每个间距期分为三段，求每一段的数值和$\sum_1 Y_t,\sum_2Y_t,\sum_3 Y_t$,

然后用这三段值解出参数

最小二乘估计

用最优化方法求：

$argmin\sum (y_i-\hat y)^2$

方法见于另一篇博客最小二乘估计

1.2平滑法

基本思想是：时间序列是某种基本变动和随机误差的叠加。平滑的目的在于消除随机误差。

分类：

移动平均法

指数平滑法

1.2.1移动平均法

简单平均法

用以前所有数的平均值，预测下一个数

$\hat Y_{t+1}= \sum\limits_{i=1}^T Y_i / T $

简单移动平均法

在简单平均法中，当T比较大时，早期的数据作用已经不大。

因此用固定的平均期数。

$\hat Y_{t+1}=\sum\limits_{i=t-T+1}^t Y_i / T $

等价于：

$\hat Y_{t+1}=\hat Y_t +\dfrac{1}{T}(Y_t-Y_{t-N})$

加权移动平均法

\(\hat Y{t+1}= \dfrac{\sum\limits_{i=1}^T \alpha_i Y_i}{\sum\limits_{i=1}^T \alpha_i}\)

移动平均法期数的确定

有周期性：以周期为期

对平滑性的要求：要求平滑，那么期多

对近期变化的敏感程度：要求敏感，那么期少

1.2.2 指数平滑法

2. 季节模型

季节周期数的识别：看自相关图，如果有季节性，那么自相关图也会显现出一定的周期性，看哪个nlag对应的自相关系数比较大，从而识别出季节数。

(如果趋势性明显，就不能用这种方法了。)

$\hat Y_t=\bar Y f_i$

其中：

$i=1,2,…,12$或$i=1,2,3,4$，表示每个期限中的第i个

$\hat Y$是所有期的平均

(如果有理由相信每个周期情况一样，用所有期的平均。如果有理由相信最近n个周期情况一样，用最近n个周期。如果有理由相信最近一周期与以往不同，用上一期回溯一个周期作为平均。)

$f_i$是同期所有数的平均/总平均.

例如，所有的1月份的平均/总平均，就是$f_1$

例子

乘法模型

$\hat Y=(a+bt)f_i$

其中，

$(a+bt)$是趋势部分

对参数估计时，可以用经验法。

也可以用OLS法，

$f_i=\dfrac{Y_i+Y_{i+T}+…+F_{i+(m-1)T}}{m}$

m是季节个数。例如，年数。

T是每个季节的长度。

例如原始数据为季度数据时，T=4。原始数据为月度数据时，T=12

$f_i$由公式给出，还需要对趋势部分$(a+bt)$估计：

可以用经验法。

也可以用OLS法，估计$V=a+bt$

加法模型

$\hat Y=(a+bt)+f_i$

$f_i$的定义同季节交乘趋向模型，$f_i=\dfrac{Y_i+Y_{i+T}+…+F_{i+(m-1)T}}{m}$

与季节交乘趋向模型的区别似乎是乘法模型和加法模型的区别？这个存疑

Python实现