【DL】第 1 部分:神经网络和深度学习
课程总结
以下是课程链接中给出的课程摘要:
如果你想打入尖端人工智能领域,本课程将帮助你实现这一目标。深度学习工程师备受追捧,掌握深度学习会给你带来无数新的职业机会。深度学习也是一种新的“超级力量”,可以让您构建几年前还不可能构建的 AI 系统。
在本课程中,您将学习深度学习的基础知识。完成本课程后,您将:
了解推动深度学习的主要技术趋势
能够构建、训练和应用完全连接的深度神经网络
了解如何实现高效(矢量化)神经网络
了解神经网络架构中的关键参数
本课程还向您介绍深度学习的实际工作原理,而不是仅提供粗略或表面的描述。所以在完成它之后,你将能够将深度学习应用到你自己的应用程序中。如果你正在寻找 AI 领域的工作,完成本课程后,你还将能够回答基本的面试问题。
深度学习简介
能够解释推动深度学习兴起的主要趋势,并了解它在当今的应用领域和应用方式。
什么是(神经网络)NN?
单个神经元 == 线性回归
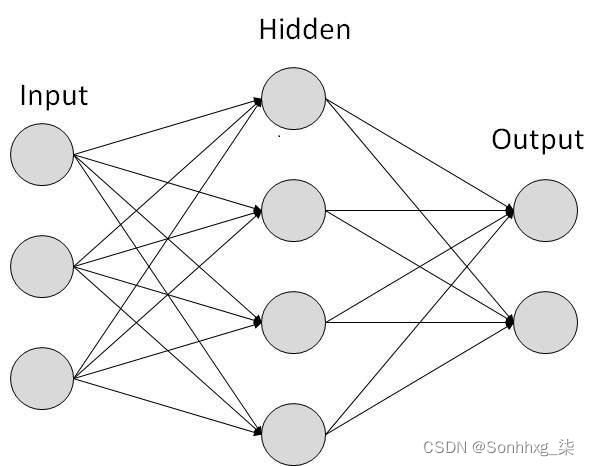
简单的神经网络图:
图片取自tutorialspoint.com
RELU 代表整流线性单元,是目前最流行的激活函数,可以让深度神经网络训练得更快。
隐藏层自动预测输入之间的连接,这就是深度学习擅长的。
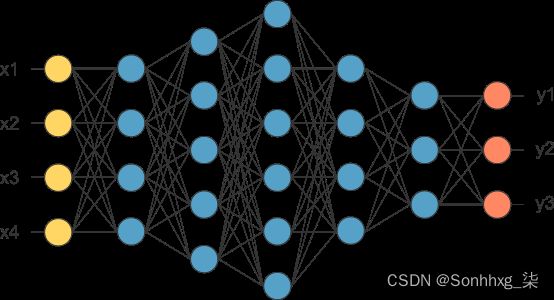
Deep NN 由更多隐藏层(Deeper layers)组成
图片取自opennn.net
每个输入都将连接到隐藏层,神经网络将决定连接。
监督学习意味着我们有 (X,Y),我们需要得到将 X 映射到 Y 的函数。
使用神经网络进行监督学习
用于监督学习的不同类型的神经网络包括:
CNN 或卷积神经网络(在计算机视觉中很有用)
RNN 或递归神经网络(在语音识别或 NLP 中很有用)
标准神经网络(对结构化数据有用)
混合/自定义 NN 或 NN 类型的集合
结构化数据就像数据库和表格。
非结构化数据如https://raw.githubusercontent.com/ashishpatel26/DeepLearning.ai-Summary/master/1-%20Neural%20Networks%20and%20Deep%20Learning/Images/、视频、音频和文本。
结构化数据能带来更多收益,因为公司依赖于对其大数据的预测。
为什么深度学习会起飞?
深度学习正在起飞有 3 个原因:
数据:
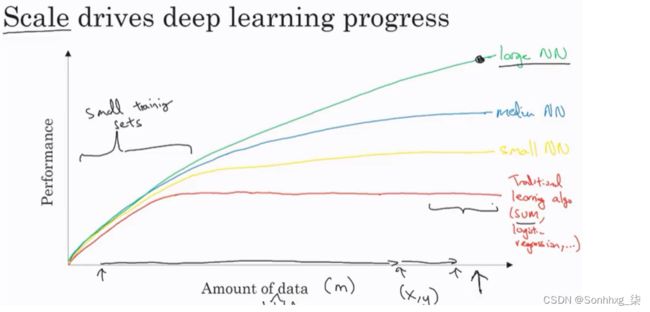
使用这张图片我们可以得出结论:
对于小数据,NN 可以作为线性回归或 SVM(支持向量机)执行
对于大数据,小型 NN 优于 SVM
对于大数据,大 NN 优于中等 NN 优于小 NN。
希望我们有很多数据,因为世界对计算机的使用越来越多
手机
IOT(物联网)
计算:
GPU。
强大的 CPU。
分布式计算。
专用集成电路
算法:
创造性算法的出现改变了神经网络的工作方式。
例如,在训练 NN 时使用 RELU 函数比使用 SIGMOID 函数好得多,因为它有助于解决梯度消失问题。
神经网络基础
学习使用神经网络思维方式设置机器学习问题。学习使用矢量化来加速您的模型。
二进制分类
他主要是在讲如何做逻辑回归来做一个二元分类器。
图片取自3.bp.blogspot.com
他谈到了一个知道当前图像是否包含猫的例子。
这里有一些符号:
M is the number of training vectors
Nx is the size of the input vector
Ny is the size of the output vector
X(1) is the first input vector
Y(1) is the first output vector
X = [x(1) x(2).. x(M)]
Y = (y(1) y(2).. y(M))
我们将在本课程中使用 python。
在 NumPy 中,我们可以快速可靠地创建矩阵并对其进行运算。
逻辑回归
算法用于2类的分类算法。
方程式:
简单方程式: y = wx + b
如果 x 是向量:y = w(transpose)x + b
如果我们需要 y 在 0 和 1 之间(概率):y = sigmoid(w(transpose)x + b)
在某些符号中,这可能会被使用:y = sigmoid(w(transpose)x)
虽然b是w0,w但我们添加了x0 = 1。但我们不会在课程中使用这种表示法(Andrew 说第一种表示法更好)。
在二进制分类Y中,必须介于0和之间1。
在最后一个等式w中是一个向量Nx并且b是一个实数
逻辑回归代价函数
第一个损失函数是平方根误差: L(y',y) = 1/2 (y' - y)^2
但是我们不会使用这种表示法,因为它会导致我们遇到非凸的优化问题,这意味着它包含局部最优点。
这是我们将使用的功能:L(y',y) = - (y*log(y') + (1-y)*log(1-y'))
要解释最后一个功能,请看:
if y = 1==> L(y',1) = -log(y') ==> 我们想y'成为最大的 ==> y'最大值是 1
if y = 0==> L(y',0) = -log(1-y')==> 我们想1-y'成为最大的 ==>y'尽可能小,因为它只能有 1 个值。
那么成本函数将是:J(w,b) = (1/m) * Sum(L(y'[i],y[i]))
损失函数计算单个训练样本的误差;成本函数是整个训练集损失函数的平均值。
梯度下降
我们想要预测w并b最小化成本函数。
我们的成本函数是凸的。
首先我们将w和初始化b为 0,0 或在凸函数中将它们初始化为随机值,然后尝试改进这些值以达到最小值。
在逻辑回归中,人们总是使用 0,0 而不是随机数。
梯度下降算法重复:w = w - alpha * dw 其中 alpha 是学习率并且dw是w(Change to w) 的导数 导数也是斜率w
看起来像贪心算法。导数给了我们改进参数的方向。
我们将实施的实际方程式:
w = w - alpha * d(J(w,b) / dw) (函数在w方向倾斜多少)
b = b - alpha * d(J(w,b) / db) (函数在 d 方向上倾斜了多少)
衍生品
我们将讨论一些必需的微积分。
你不需要成为微积分极客也能掌握深度学习,但你需要从中学到一些技能。
直线的导数是它的斜率。
前任。f(a) = 3a d(f(a))/d(a) = 3
如果a = 2那么f(a) = 6
如果我们稍微移动一点a = 2.001则f(a) = 6.003意味着我们将导数(斜率)乘以移动的区域并将其添加到最后的结果。
更多衍生品示例
f(a) = a^2 ==>d(f(a))/d(a) = 2a
a = 2 ==>f(a) = 4
a = 2.0001==>f(a) = 4.0004大约。
f(a) = a^3 ==>d(f(a))/d(a) = 3a^2
f(a) = log(a) ==>d(f(a))/d(a) = 1/a
总而言之,导数是斜率,函数中不同点的斜率不同,这就是导数是函数的原因。
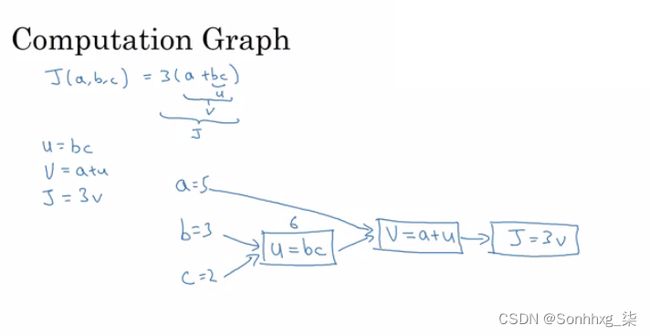
计算图
它是一个从左到右组织计算的图表。
带有计算图的导数
微积分链式法则说: If x -> y -> z (x effect y and y effects z) Thend(z)/d(x) = d(z)/d(y) * d(y)/d(x)
该视频说明了一个很大的例子。
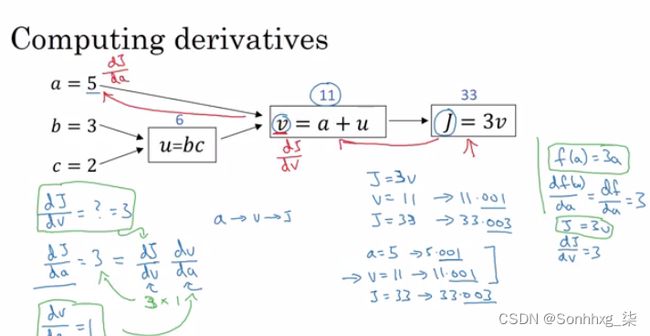
我们从右到左计算图上的导数,这会容易得多。
dvar指最终输出变量对各种中间量的导数。
逻辑回归梯度下降
x1在视频中,他讨论了具有两个特征和的一个样本的梯度下降示例的导数x2。
m 个例子的梯度下降
假设我们有这些变量:
X1 Feature
X2 Feature
W1 Weight of the first feature.
W2 Weight of the second feature.
B Logistic Regression parameter.
M Number of training examples
Y(i) Expected output of i所以我们有:
然后从右到左我们将计算与结果相比的推导:
d(a) = d(l)/d(a) = -(y/a) + ((1-y)/(1-a))
d(z) = d(l)/d(z) = a - y
d(W1) = X1 * d(z)
d(W2) = X2 * d(z)
d(B) = d(z)从上面我们可以总结出逻辑回归伪代码:
J = 0; dw1 = 0; dw2 =0; db = 0; # Devs.
w1 = 0; w2 = 0; b=0; # Weights
for i = 1 to m
# Forward pass
z(i) = W1*x1(i) + W2*x2(i) + b
a(i) = Sigmoid(z(i))
J += (Y(i)*log(a(i)) + (1-Y(i))*log(1-a(i)))
# Backward pass
dz(i) = a(i) - Y(i)
dw1 += dz(i) * x1(i)
dw2 += dz(i) * x2(i)
db += dz(i)
J /= m
dw1/= m
dw2/= m
db/= m
# Gradient descent
w1 = w1 - alpa * dw1
w2 = w2 - alpa * dw2
b = b - alpa * db上面的代码应该运行一些迭代以最小化错误。
所以会有两个内循环来实现逻辑回归。
矢量化在深度学习中对于减少循环非常重要。在最后的代码中,我们可以使用矢量化一步完成整个循环!
矢量化
当数据集很大时,深度学习会大放异彩。但是 for 循环会让你等待很多时间才能得到结果。这就是为什么我们需要矢量化来摆脱一些 for 循环。
NumPy 库(点)函数默认使用矢量化。
向量化可以通过 SIMD 操作在 CPU 或 GPU 上完成。但它在 GPU 上更快。
尽可能避免 for 循环。
大多数 NumPy 库方法都是矢量化版本。
向量化逻辑回归
我们将使用一个 for 循环然后不使用任何 for 循环来实现逻辑回归。
作为输入,我们有一个矩阵X及其[Nx, m]和一个矩阵Y及其[Ny, m]。
然后我们将计算 instance [z1,z2...zm] = W' * X + [b,b,...b]。这可以用 python 写成:
Z = np.dot(W.T,X) + b # Vectorization, then broadcasting, Z shape is (1, m)
A = 1 / 1 + np.exp(-Z) # Vectorization, A shape is (1, m)向量化逻辑回归的梯度输出:
dz = A - Y # Vectorization, dz shape is (1, m)
dw = np.dot(X, dz.T) / m # Vectorization, dw shape is (Nx, 1)
db = dz.sum() / m # Vectorization, db shape is (1, 1)关于 Python 和 NumPy 的注释
在 NumPy 中,在对行obj.sum(axis = 0)求和的同时对列obj.sum(axis = 1)求和。
在 NumPy 中,obj.reshape(1,4)通过广播值改变矩阵的形状。
Reshape 在计算中很便宜,所以把它放在你不确定计算的任何地方。
当您使用与运算不匹配的矩阵执行矩阵运算时,广播会起作用,在这种情况下,NumPy 会通过广播值自动使形状为运算做好准备。
广播的一般原则。如果你有一个 (m,n) 矩阵并且你用 (1,n) 矩阵加 (+) 或减 (-) 或乘 (*) 或除 (/),那么这会将它复制 m 次到一个 ( m,n) 矩阵。如果您将这些操作与 (m , 1) 矩阵一起使用,则相同,那么这会将其复制 n 次到 (m, n) 矩阵中。然后明智地应用除法元素的加法、减法和乘法。
消除代码中所有奇怪错误的一些技巧:
如果您没有指定矢量的形状,它将变成 的形状,(m,)转置操作将不起作用。你必须重塑它(m, 1)
尽量不要在 ANN 中使用秩一矩阵
不要犹豫,使用它assert(a.shape == (5,1))来检查您的矩阵形状是否符合要求。
如果您找到了一级矩阵,请尝试对其运行重塑。
Jupyter / IPython notebooks 是 python 中非常有用的库,可以轻松地同时集成代码和文档。它在浏览器中运行,不需要 IDE 即可运行。
要打开 Jupyter Notebook,请打开命令行并调用:jupyter-notebookIt should be installed to work。
计算 Sigmoid 的导数:
s = sigmoid(x)
ds = s * (1 - s) # derivative using calculus要使图像(width,height,depth)成为矢量,请使用:
v = image.reshape(image.shape[0]*image.shape[1]*image.shape[2],1) #reshapes the image.输入矩阵归一化后梯度下降收敛得更快。
一般注意事项
构建神经网络的主要步骤是:
定义模型结构(例如输入特征和输出的数量)
初始化模型的参数。
环形。
计算电流损耗(前向传播)
计算电流梯度(反向传播)
更新参数(梯度下降)
预处理数据集很重要。
调整学习率(这是“超参数”的一个例子)可以对算法产生很大的影响。
kaggle.com是数据集和竞赛的好地方。
Pieter Abbeel是深度强化学习领域的佼佼者之一。
浅层神经网络
学习使用前向传播和反向传播构建具有一个隐藏层的神经网络。
神经网络概述
在逻辑回归中,我们有:
X1 \
X2 ==> z = XW + B ==> a = Sigmoid(z) ==> l(a,Y)
X3 /在一层的神经网络中,我们将有:
X1 \
X2 => z1 = XW1 + B1 => a1 = Sigmoid(z1) => z2 = a1W2 + B2 => a2 = Sigmoid(z2) => l(a2,Y)
X3 /X是输入向量(X1, X2, X3),Y是输出变量(1x1)
NN 是逻辑回归对象的堆栈。
神经网络表示
我们将定义具有一个隐藏层的神经网络。
NN 包含输入层、隐藏层、输出层。
隐藏层意味着我们在训练集中看不到这些层。
a0 = x(输入层)
a1将代表隐藏神经元的激活。
a2将代表输出层。
我们正在谈论 2 层 NN。输入层不计算在内。
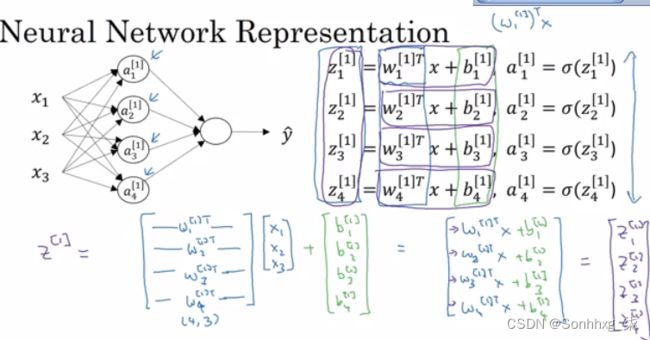
计算神经网络的输出
隐藏层方程:
以下是关于最后一张图片的一些信息:
noOfHiddenNeurons = 4
Nx = 3
变量的形状:
W1是第一个隐藏层的矩阵,它的形状为(noOfHiddenNeurons,nx)
b1是第一个隐藏层的矩阵,它的形状为(noOfHiddenNeurons,1)
z1是方程的结果z1 = W1*X + b,它的形状为(noOfHiddenNeurons,1)
a1是方程的结果a1 = sigmoid(z1),它的形状为(noOfHiddenNeurons,1)
W2是第二个隐藏层的矩阵,它的形状为(1,noOfHiddenNeurons)
b2是第二个隐藏层的矩阵,它的形状为(1,1)
z2是方程的结果z2 = W2*a1 + b,它的形状为(1,1)
a2是方程的结果a2 = sigmoid(z2),它的形状为(1,1)
跨多个示例向量化
2 层 NN 的前向传播伪代码:
for i = 1 to m
z[1, i] = W1*x[i] + b1 # shape of z[1, i] is (noOfHiddenNeurons,1)
a[1, i] = sigmoid(z[1, i]) # shape of a[1, i] is (noOfHiddenNeurons,1)
z[2, i] = W2*a[1, i] + b2 # shape of z[2, i] is (1,1)
a[2, i] = sigmoid(z[2, i]) # shape of a[2, i] is (1,1)让我们说我们有X形状(Nx,m)。所以新的伪代码:
Z1 = W1X + b1 # shape of Z1 (noOfHiddenNeurons,m)
A1 = sigmoid(Z1) # shape of A1 (noOfHiddenNeurons,m)
Z2 = W2A1 + b2 # shape of Z2 is (1,m)
A2 = sigmoid(Z2) # shape of A2 is (1,m)如果您总是注意到 m 是列数。
在最后一个例子中,我们可以调用X= A0。所以上一步可以改写为:
Z1 = W1A0 + b1 # shape of Z1 (noOfHiddenNeurons,m)
A1 = sigmoid(Z1) # shape of A1 (noOfHiddenNeurons,m)
Z2 = W2A1 + b2 # shape of Z2 is (1,m)
A2 = sigmoid(Z2) # shape of A2 is (1,m)激活函数
到目前为止,我们使用的是 sigmoid,但在某些情况下,其他函数会好很多。
Sigmoid 会导致我们遇到梯度下降问题,其中更新非常低。
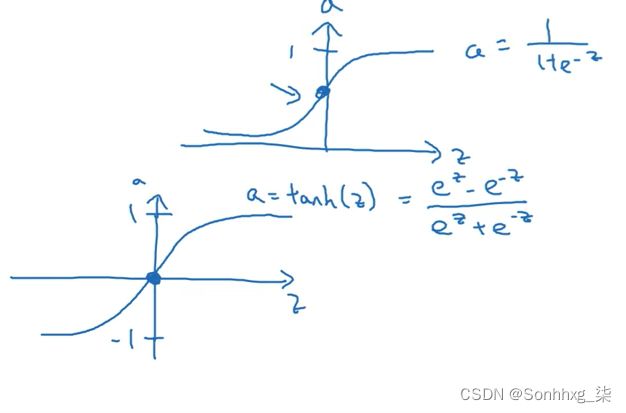
Sigmoid 激活函数范围是 [0,1] A = 1 / (1 + np.exp(-z)) # Where z is the input matrix
Tanh 激活函数范围是 [-1,1](S 型函数的移位版本)
在 NumPy 中,我们可以使用以下方法之一实现 Tanh: A = (np.exp(z) - np.exp(-z)) / (np.exp(z) + np.exp(-z)) # Where z is the input matrix
或者 A = np.tanh(z) # Where z is the input matrix
事实证明,对于隐藏单元,tanh 激活通常比 sigmoid 激活函数效果更好,因为它的输出均值更接近于零,因此它可以更好地将数据集中到下一层。
Sigmoid 或 Tanh 函数的缺点是,如果输入太小或太高,斜率将接近于零,这将导致梯度下降问题。
RELU 函数是解决慢梯度体面问题的流行激活函数之一。 RELU = max(0,z) # so if z is negative the slope is 0 and if z is positive the slope remains linear.
所以这里有一些选择激活函数的基本规则,如果你的分类在 0 和 1 之间,使用输出激活作为 sigmoid,其他作为 RELU。
Leaky RELU 激活函数与 RELU 的不同之处在于,如果输入为负,则斜率会非常小。它像 RELU 一样工作,但大多数人使用 RELU。 Leaky_RELU = max(0.01z,z) #the 0.01 can be a parameter for your algorithm.
在 NN 中,您将做出很多选择,例如:
没有隐藏层。
每个隐藏层中的神经元数量。
学习率。(最重要的参数)
激活函数。
和别的..
事实证明,没有指导方针。例如,您应该尝试所有激活函数。
为什么需要非线性激活函数?
如果我们从我们的算法中删除激活函数,则可以称为线性激活函数。
线性激活函数将输出线性激活
无论你添加什么隐藏层,激活总是像逻辑回归一样是线性的(所以它在很多复杂问题中没用)
您可以在一个地方使用线性激活函数 - 如果输出是实数(回归问题),则在输出层。但即使在这种情况下,如果输出值是非负的,您也可以改用 RELU。
激活函数的导数
Sigmoid激活函数的推导:
g(z) = 1 / (1 + np.exp(-z))
g'(z) = (1 / (1 + np.exp(-z))) * (1 - (1 / (1 + np.exp(-z))))
g'(z) = g(z) * (1 - g(z))Tanh激活函数的推导:
g(z) = (e^z - e^-z) / (e^z + e^-z)
g'(z) = 1 - np.tanh(z)^2 = 1 - g(z)^2RELU激活函数推导:
g(z) = np.maximum(0,z)
g'(z) = { 0 if z < 0
1 if z >= 0 }leaky RELU激活函数的推导:
g(z) = np.maximum(0.01 * z, z)
g'(z) = { 0.01 if z < 0
1 if z >= 0 }神经网络的梯度下降
在本节中,我们将了解神经网络的完整反向传播(只是没有解释的方程式)。
梯度下降算法:
神经网络参数:
n[0] = Nx
n[1] = NoOfHiddenNeurons
n[2] = NoOfOutputNeurons = 1
W1形状是(n[1],n[0])
b1形状是(n[1],1)
W2形状是(n[2],n[1])
b2形状是(n[2],1)
代价函数I = I(W1, b1, W2, b2) = (1/m) * Sum(L(Y,A2))
然后梯度下降:
Repeat:
Compute predictions (y'[i], i = 0,...m)
Get derivatives: dW1, db1, dW2, db2
Update: W1 = W1 - LearningRate * dW1
b1 = b1 - LearningRate * db1
W2 = W2 - LearningRate * dW2
b2 = b2 - LearningRate * db2前向传播:
Z1 = W1A0 + b1 # A0 is X
A1 = g1(Z1)
Z2 = W2A1 + b2
A2 = Sigmoid(Z2) # Sigmoid because the output is between 0 and 1反向传播(推导):
dZ2 = A2 - Y # derivative of cost function we used * derivative of the sigmoid function
dW2 = (dZ2 * A1.T) / m
db2 = Sum(dZ2) / m
dZ1 = (W2.T * dZ2) * g'1(Z1) # element wise product (*)
dW1 = (dZ1 * A0.T) / m # A0 = X
db1 = Sum(dZ1) / m
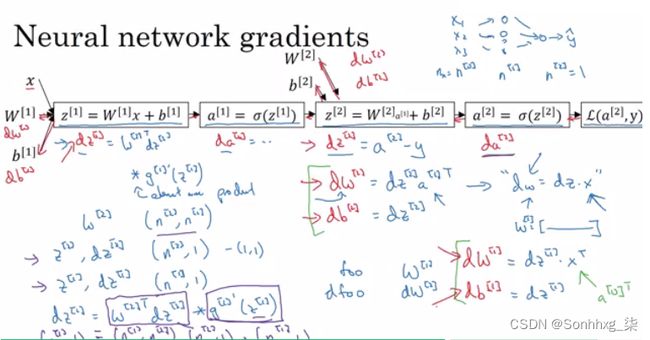
# Hint there are transposes with multiplication because to keep dimensions correct我们如何推导出反向传播的 6 个方程:
随机初始化
在逻辑回归中随机初始化权重并不重要,而在 NN 中我们必须随机初始化它们。
如果我们在 NN 中用零初始化所有权重,它将不起作用(用零初始化偏差是可以的):
所有隐藏单元将完全相同(对称)——计算完全相同的函数
在每次梯度下降迭代中,所有隐藏单元将始终更新相同的
为了解决这个问题,我们用一个小的随机数初始化 W:
W1 = np.random.randn((2,2)) * 0.01 # 0.01 to make it small enough
b1 = np.zeros((2,1)) # its ok to have b as zero, it won't get us to the symmetry breaking problem我们需要小值,因为在 sigmoid(或 tanh)中,例如,如果权重太大,即使在训练开始时也更有可能以非常大的 Z 值结束。这会导致您的 tanh 或 sigmoid 激活功能饱和,从而减慢学习速度。如果您在整个神经网络中没有任何 sigmoid 或 tanh 激活函数,这就不是什么问题。
常数 0.01 对于 1 个隐藏层网络是可以的,但如果 NN 很深,这个数字可以改变,但它总是一个小数字。
深度神经网络
了解深度学习的关键计算,使用它们构建和训练深度神经网络,并将其应用于计算机视觉。
深度L层神经网络
浅层神经网络是具有一层或两层的神经网络。
深度神经网络是具有三层或更多层的神经网络。
我们将使用符号L来表示 NN 中的层数。
n[l]是特定层中神经元的数量l。
n[0]表示输入层的神经元个数。n[L]表示输出层神经元的数量。
g[l]是激活函数。
a[l] = g[l](z[l])
w[l]权重用于z[l]
x = a[0],a[l] = y'
这些是我们将用于深度神经网络的符号。
所以我们有:
n形状向量(1, NoOfLayers+1)
g形状向量(1, NoOfLayers)
w基于前一层和当前层上的神经元数量的不同形状列表。
b基于当前层上神经元数量的不同形状列表。
深度网络中的前向传播
一个输入的前向传播一般规则:
z[l] = W[l]a[l-1] + b[l]
a[l] = g[l](a[l])输入的前向传播一般规则m:
Z[l] = W[l]A[l-1] + B[l]
A[l] = g[l](A[l])如果没有 for 循环,我们无法计算整个层的前向传播,因此可以在此处使用 for 循环。
矩阵的维度非常重要,您需要弄清楚。
让你的矩阵维度正确
调试矩阵维度的最佳方法是使用铅笔和纸。
的维数W为(n[l],n[l-1])。可以从右到左思考。
的维度b是(n[l],1)
dw具有与 相同的形状W,而db与 具有相同的形状b
Z[l], A[l]、dZ[l]和的维数dA[l] 是(n[l],m)
为什么深度表征?
为什么深度神经网络效果好,我们将在本节中讨论这个问题。
深度神经网络使与数据的关系从简单到复杂。在每一层中,它都试图与前一层建立关系。例如:
人脸识别应用:
图片==>边缘==>面部零件==>面部==>所需面部
语音识别应用:
音频 ==> 低级声音特征,如 (sss,bb) ==> 音素 ==> 单词 ==> 句子
神经研究人员认为深度神经网络像大脑一样“思考”(简单 ==> 复杂)
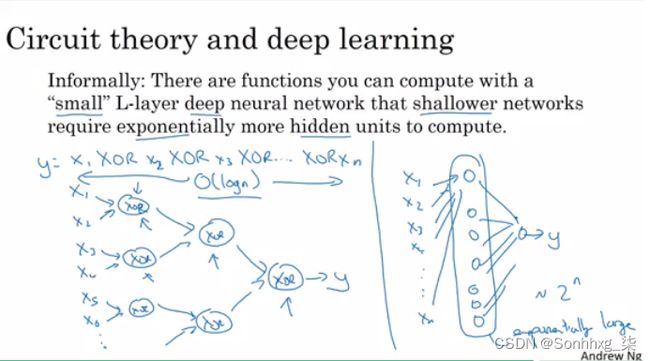
电路理论与深度学习:
在启动应用程序时,不要直接从几十个隐藏层开始。尝试最简单的解决方案(例如逻辑回归),然后尝试浅层神经网络等。
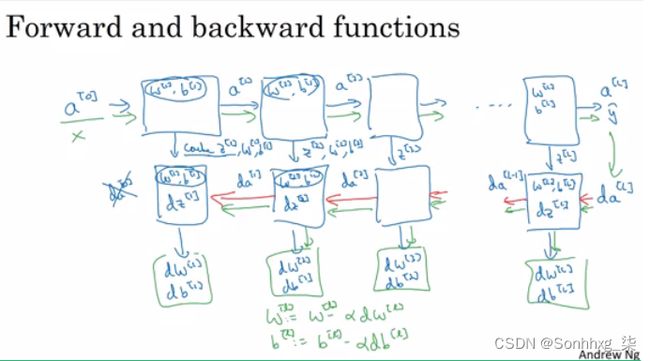
深度神经网络的构建块
l 层的前向和反向传播:
深度神经网络块:
向前和向后传播
l层前向传播的伪代码:
Input A[l-1]
Z[l] = W[l]A[l-1] + b[l]
A[l] = g[l](Z[l])
Output A[l], cache(Z[l])l层反向传播的伪代码:
Input da[l], Caches
dZ[l] = dA[l] * g'[l](Z[l])
dW[l] = (dZ[l]A[l-1].T) / m
db[l] = sum(dZ[l])/m # Dont forget axis=1, keepdims=True
dA[l-1] = w[l].T * dZ[l] # The multiplication here are a dot product.
Output dA[l-1], dW[l], db[l]如果我们使用了损失函数,那么:
dA[L] = (-(y/a) + ((1-y)/(1-a)))参数与超参数
NN 的主要参数是W和b
超参数(控制算法的参数)是这样的:
学习率。
迭代次数。
隐藏层数L。
隐藏单元数n。
激活函数的选择。
您必须自己尝试超参数的值。
在 DL 和 ML 的早期,学习率通常被称为参数,但它确实是(现在每个人都这样称呼它)超参数。
在下一个课程中,我们将看到如何优化超参数。
这和大脑有什么关系
“它就像大脑”这样的类比,实在是过于简单化了。
单个逻辑单元和大脑中的单个神经元之间有一个非常简单的类比。
今天没有人了解人脑神经元是如何工作的。
今天没有人确切地知道大脑中有多少个神经元。
Andrew 认为深度学习非常擅长学习非常灵活、复杂的函数来学习 X 到 Y 的映射,学习输入输出映射(监督学习)。
与其他应用深度学习的学科相比,计算机视觉领域从人脑中获得的灵感更多一些。
NN 是大脑如何工作的一个小代表。最接近人脑的模型是计算机视觉(CNN)