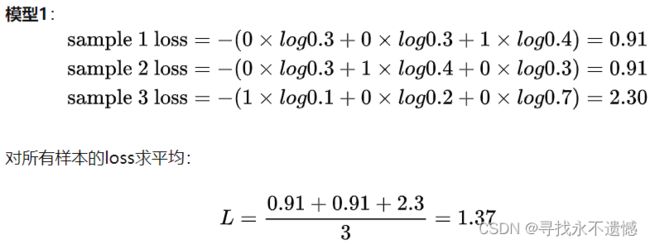【MSE/BCE/CE】均方差、交叉熵损失函数理解

1 均方误差(Mean Squared Error, MSE)

1.1 MSE介绍

MSE公式：

其中：

• n为样本的个数
• $y_i$是真实数据
• ${\hat{y}}_i$表示预测的数据

误差越接近于0，说明效果越好。

1.2 MSE为何不常用于分类

主要原因是在分类问题中，使用sigmoid/softmax得到概率，配合MSE损失函数时，采用梯度下降法进行学习时，会出现模型一开始训练时，学习速率非常慢的情况。

1.3 那什么常用于分类呢?

交叉熵损失常用于分类，交叉熵包括BCE和CE两种，下面分别介绍。

2 二值交叉熵损失(Binary Cross Entropy Loss, BCE)

2.1 BCE介绍

用于二分类（用于多分类时，针对每一个类别，都当作一个二分类来处理，是不是这个类别，属于这个类别的概率。区别于CE，CE用的是softmax，每个类别互斥，所有类别概率和为1，而BCE所有概率和不一定等于1，类别之间不互斥），模型结果只有两种情况(两个类别)，针对一个样本，假设得到的预测概率一类为$p$，另一类为$1-p$，此时BCE公式为：

其中：

• log的底数为e
• $y_i$表示样本 i 的标签，正类为1，负类为0(注：BCE并不是只能学习0或1的label)，使用的是one_hot编码
• $p_i$表示样本 i 预测为正类的概率，是经过sigmoid后的数
• N表示样本个数，这里是取了均值的

这样，当样本label为0的时候，公式前半部分为0，$p_i$ 需要尽可能为0才能使后半部分数值更小；
当样本label为1时，后半部分为0，$p_i$ 需要尽可能为1才能使前半部分的值更小，这样就达到了让$p_i$ 尽量靠近样本label的目的。

通常情况下，使用BCELoss，网络只需输出一个节点，即所有框对所有类别的二分类概率的均值，而CE Loss(Cross Entropy Loss)，有n_class个类别，网络最终输出n_class个节点。

2.2 pytorch中的BCELoss与自己实现的区别

torch.nn.BCELoss(input: Tensor, target: Tensor) -> Tensor

实例：

import torch
import numpy as np

# ------------------------------------------# 
#   没有reduction='none'，输出的loss是一个均值
# ------------------------------------------#
loss = torch.nn.BCELoss(reduction='none')
loss_one_mean_value = torch.nn.BCELoss()

predict = [[0.1,0.8,0.9], [0.2,0.7,0.8]]
predict_tensor = torch.tensor(predict, requires_grad=True)
# ----------------------------------------------------------------------#
#   为何不是0 or 1 这种int，后面要加个点？
#   答：Only Tensors of floating point and complex dtype can require gradients
# ----------------------------------------------------------------------#
target = [[0.,0.,1.], [0.,0.,1.]]
target_tensor = torch.tensor(target, requires_grad=True)

l = loss(input=predict_tensor, target=target_tensor)
l_one_mean_value = loss_one_mean_value(input=predict_tensor, target=target_tensor)
# -------------------------------# 
#   .detach()把梯度信息去掉
#   .numpy()转成numpy数组
#   np.round(a,5)保留5位小数
# -------------------------------#
print("torch.nn.BCELoss_loss_output: ", np.round(l.detach().numpy(), 5))
print("torch.nn.BCELoss_loss_one_mean_value: ", np.round(l_one_mean_value.detach().numpy(), 5))
print('-------------------------------------------------------------')
print('predict_tensor: ', predict_tensor)
print('target_tensor: ', target_tensor)
print('loss_output: ', l)
print('loss_output_detach: ', l.detach())
print('-------------------------------------------------------------')


def bce(p,g):
    return np.round(-(g*np.log(p) + (1-g)*np.log(1-p)), 5)

predict_np = np.array(predict)
target_np = np.array(target)
print("self_bce_loss_output: ", bce(predict_np, target_np))

输出：

torch.nn.BCELoss_loss_output:  [[0.10536 1.60944 0.10536]
 [0.22314 1.20397 0.22314]]
torch.nn.BCELoss_loss_one_mean_value:  0.5784
-------------------------------------------------------------
predict_tensor:  tensor([[0.1000, 0.8000, 0.9000],
        [0.2000, 0.7000, 0.8000]], requires_grad=True)
target_tensor:  tensor([[0., 0., 1.],
        [0., 0., 1.]], requires_grad=True)
loss_output:  tensor([[0.1054, 1.6094, 0.1054],
        [0.2231, 1.2040, 0.2231]], grad_fn=)
loss_output_detach:  tensor([[0.1054, 1.6094, 0.1054],
        [0.2231, 1.2040, 0.2231]])
-------------------------------------------------------------
self_bce_loss_output:  [[0.10536 1.60944 0.10536]
 [0.22314 1.20397 0.22314]]

应用时，通常还有个l.backward()

3 交叉熵损失(Cross Entropy Loss, CE)

3.1 CE介绍

用于多分类(二分类的扩展而已)，CE计算公式为：

其中：

• log的底数为e
• $y_{ic}$表示样本 i 的标签，这是一个符号函数，如果样本 i 的真实类别等于c，则取1，否则取0
• $p_{ic}$表示样本 i 预测为 c类 的概率
• N表示样本个数
• M表示类别数量

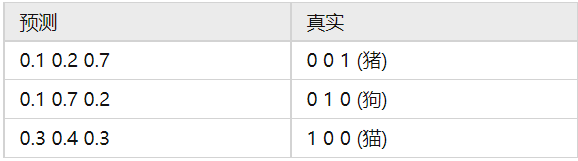
举个例子：
两个模型，三个类别，明显模型2好些。

• 模型1：
  
  
• 模型2：
  
  
  损失也是模型2的小些。

3.2 分类损失到底怎么得到的

交叉熵损失函数常用于神经网络分类问题中，由于交叉熵涉及到计算每个类别的概率，所以交叉熵一般都和sigmoid(或softmax)函数一起出现。

以神经网络最后一层的输出，来看一下整个模型预测、获得损失的流程：

• 神经网络最后一层得到每个类别的得分scores（也叫logits）；
• 该得分经过sigmoid(或softmax)函数获得概率输出；
• 模型预测的类别概率输出与真实类别的one hot形式进行交叉熵损失函数的计算。

3.3 pytorch中的CELoss

torch.nn.CrossEntropyLoss(input: Tensor, target: Tensor) -> Tensor:

实例： input和target都和BCE一样，这儿区别在哪里，还得再思考下

import torch
import torch.nn as nn

m = nn.Sigmoid()
loss = nn.CrossEntropyLoss()
input = torch.tensor([[-0.5255, -0.9176,  0.1117],
        [ 0.8469, -0.3685, -1.2900],
        [ 1.1795, -2.0813,  1.8317]], requires_grad=True)
target = torch.tensor([[1., 0., 0.],
        [0., 1., 1.],
        [0., 0., 1.]])
output = loss(m(input), target)
output.backward()

print('input', input)
print('-----------------------------')
print('target', target)
print('-----------------------------')
print('m(input)', m(input))
print('-----------------------------')
print('output', output)

输出：

input tensor([[-0.5255, -0.9176,  0.1117],
        [ 0.8469, -0.3685, -1.2900],
        [ 1.1795, -2.0813,  1.8317]], requires_grad=True)
-----------------------------
target tensor([[1., 0., 0.],
        [0., 1., 1.],
        [0., 0., 1.]])
-----------------------------
m(input) tensor([[0.3716, 0.2854, 0.5279],
        [0.6999, 0.4089, 0.2159],
        [0.7649, 0.1109, 0.8620]], grad_fn=)
-----------------------------
output tensor(1.4965, grad_fn=)

4 解释BCE并不是只能学习0或1的label

BCE虽然总是用来学习0/1分布，即二分类问题，但不是0/1两个数，只要在0~1之间的数也都能学习。原因从BCE的公式聊起：

5 参考链接

https://blog.csdn.net/weixin_37724529/article/details/107084970
https://www.cnblogs.com/dotman/p/13857843.html
https://zhuanlan.zhihu.com/p/108961272
https://zhuanlan.zhihu.com/p/35709485