ConsensusClustering及R实现

一、定义及K值选择

基本原理假设：一致性聚类通过基于重采样的方法来验证聚类合理性，其主要目的是评估聚类的稳定性。

即通过改变聚类的数据集（里面的数据全部从原始数据中抽取，也可以理解为是原始数据的子集），通过考量任意一个数据在不同样本中聚类表现的一致性来确定聚类的参数是否合适。

      第一步：从原始数据中随机抽取子集，当然子集的规模不能太小，最好是原始数据集的半数以上（这是我自己理解的，数据太少聚类的话没有意义），子集要尽量多，以确保里面的每一个数据都多次被取到（100次以上），然后，我们选择任意一种聚类方法，可以使K-means或者层次聚类，对所有的数据子集分别聚类。

     第二步：这一步的关键在于建立一个新的矩阵：consensus matrix， 我们之前说聚类的输入通常是一个distance matrix。 那么consensus matrix怎么建呢？假设有D1，D2...Dn这N个数据，那么consensus matrix是NxN 的方阵。

     D1    D2   D3...  Dn    

D1   C11  C12  C13...  C1n

D2   C21  C22  C23...  C2n

...               Cij

Dn   Cn1  Cn2  Cn3...  Cnn

 

Cij 代表的是在多次的聚类过程中，数据Di 和数据Dj 被聚到同一类里面的概率（该值在0和1之间），等于1代表100次聚类这两个数据点全部在同一个类里面，等于0代表代表100次聚类全部不在同一个类里面。

那么，好的聚类方法会得到怎么样的consensus matrix呢？对了，全部由0或1组成的方阵，代表着那些很像的数据总在一类，而不像的数据则总是不在一类，这正符合了聚类的初衷是吧。

一致性聚类中最重要的是K值的确定，以下提供了几种确定K值的方法：

1.热图

对consensus matrix做一次聚类(这里用层次聚类方便可视化），只有0和1的矩阵，就让是1的都聚在一起，而0的都分开来，用heatmap看起来就是下面这样的;

 

看起来很爽吧，这就是离得近的全部都聚在红色块里面而且分的很开。那么差的聚类就没这么好看了;

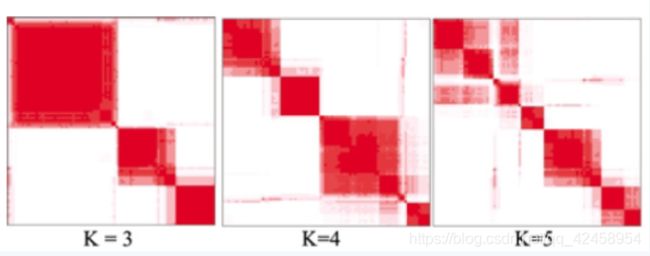
比如，上面的情况，我们取不同的k值时，显然聚类效果不同，越是干净，越是效果好；不好的聚类参数则表现出越是有很多“噪音”。

有些情况下，仅仅通过看不同参数下consensus matrix聚类出来的热图就基本可以判断怎么选择了。 

2.其他特征

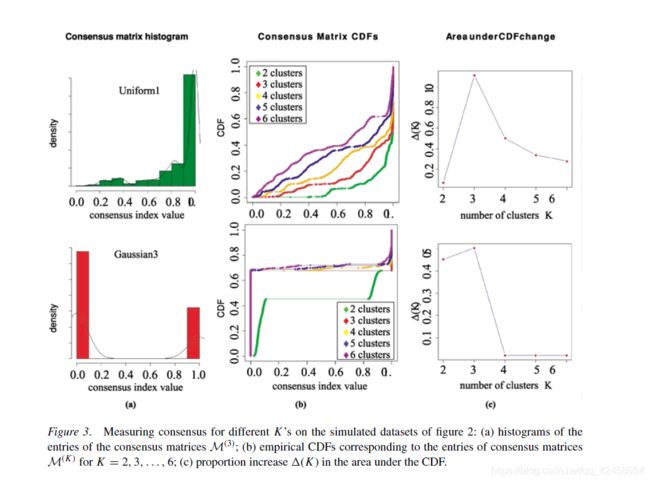
• 直方图（直方图大部分分布在0和1时，聚类效果越好，Figure 3(a) 下图）
• CDF (Cumulative Distribution Function)，此图展示了K取不同数值时的累计分布函数，用于判断K值取何值时，CDF达到近似最大值，此时的聚类分析结果最可靠，通常取CDF下降坡度小的K值。
• area under CDF change (此图展示的是K和K-1相比CDF曲线下面积的相对变化，Figure 3(c) 下图，当K=4时，曲线下面积增长幅度接近0，故3为合适的K值)

Reference：

Monti,S., et al. (2003) Consensus clustering: A resampling-based method for class discovery and visualization of gene microarray, Mach Learn,52, 91-118

二、R实现

在ConsensusClusterPlus包中实现

##使用ALL示例数据
library(ALL)
data(ALL)
d=exprs(ALL)

#筛选前5000标准差的基因
mads=apply(d,1,mad)
d=d[rev(order(mads))[1:5000],]

#sweep函数减去中位数进行标准化
d = sweep(d,1, apply(d,1,median,na.rm=T))

#一步完成聚类
library(ConsensusClusterPlus)
title=tempdir()
results = ConsensusClusterPlus(d,maxK=6,reps=50,pItem=0.8,pFeature=1,
 title=title,clusterAlg="hc",distance="pearson",seed=1262118388.71279,plot="png")

#输出K=2时的一致性矩阵
results[[2]][["consensusMatrix"]][1:5,1:5]

          [,1]      [,2]      [,3]      [,4]     [,5]
[1,] 1.0000000 1.0000000 0.8947368 1.0000000 1.000000
[2,] 1.0000000 1.0000000 0.9142857 1.0000000 1.000000
[3,] 0.8947368 0.9142857 1.0000000 0.8857143 0.969697
[4,] 1.0000000 1.0000000 0.8857143 1.0000000 1.000000
[5,] 1.0000000 1.0000000 0.9696970 1.0000000 1.000000

#hclust选项
results[[2]][["consensusTree"]]

Call:
hclust(d = as.dist(1 - fm), method = finalLinkage)

Cluster method   : average 
Number of objects: 128 

#样本分类
results[[2]][["consensusClass"]][1:5]

01005 01010 03002 04006 04007 
    1     1     1     1     1 

#计算聚类一致性 (cluster-consensus) 和样品一致性 (item-consensus)
icl <- calcICL(results, title = title,
               plot = "png")
## 返回了具有两个元素的list，然后分别查看一下
dim(icl[["clusterConsensus"]])
 [1] 20  3
icl[["clusterConsensus"]] 

dim(icl[["itemConsensus"]])
 [1] 2560    4
icl[["itemConsensus"]][1:5,] 

参考文章：http://www.360doc.com/content/20/0415/23/46752147_906313676.shtml