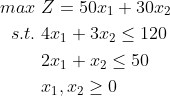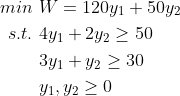线性规划的对偶问题（The Dual of LP）

目录

1.对偶问题的经济学解释(Economic Interpretation of the Dual Problem)

2.获得线性规划的对偶(Finding the Dual of an LP)

2.1 对称型对偶问题

2.2 非对称型对偶问题

3.对偶定理(The Dual Theorem)

3.1 弱对偶定理 

3.2 最优性定理 

3.3 强对偶定理 

4.互补松弛定理(Complementary Slackness) 

5.影子价格(Shadow Prices)

6.对偶单纯形法(The Dual Simplex Method)

6.1 对偶单纯形法的由来

6.2 对偶单纯形法的步骤

6.3 对偶单纯形法的三种用途

6.4 对偶单纯形法的求解案例

---

对偶理论是线性规划中最重要的理论之一，是深入了解线性规划问题结构的重要理论基础。了解线性规划与其对偶问题之间的关系，对于理解线性和非线性规划的高级专题具有重要作用。

1.对偶问题的经济学解释(Economic Interpretation of the Dual Problem)

引例1：两个家具制造商间的对话如下：

李老板：Hi，王老板，听说近来家具生意好呀，也帮帮兄弟我哦！唉！我想租您的木工和油漆工一用。咋样？价格嘛。。。好说，肯定不会让您兄弟吃亏。

（内心OS：王老板做家具赚了大钱，可惜我老李有高科技产品，却苦于没有足够的木工和油漆工咋办？只有租咯）

王老板：价格嘛。。。好商量，好商量，只是。。。。

（内心OS：家具生意还真赚钱，但是现在的手机生意这么好，不如干脆把我的木工和油漆工租给他，又能收租金又可做生意）

王老板生产桌子和椅子两种产品，桌子的单价是50元，生产一张桌子需要4个木工工时，2个油漆工工时，椅子的单价为30元，生产一把椅子需要3个木工工时，1个油漆工工时，王老板总计有120个木工工时和50个油漆工工时。

此时，王老板考虑两个问题：第一个自己用木工和油漆工最多能赚多少钱，第二个把木工和油漆工出租出去不能低于自己赚的钱（不吃亏原则），并且出租的价格要尽可能低，使得李老板可以接受（竞争性原则）

第一个：王老板的家具生产模型

将该问题称为原始线性规划问题，也称为原问题，记为（P，Primal）。该模型解决的问题是，如何利用有限的资源最大化生产收益。

第二个：王老板的资源出租模型

将该问题称为对偶线性规划问题，也称为对偶问题，记为（D，Dual）。该模型解决的问题是，如何进行资源最小化定价（竞争性原则），使得资源售卖的收益不低于自己生产所获的最大生产收益（不吃亏原则）。

这里我们仔细观察一下资源出租模型，第一条约束是讲售卖4单位木工工时和2单位油漆工时的收益要大于50，50刚好是生产一张桌子的收益，生产一张桌子正好是需要4单位木工工时和2单位油漆工工时。第一条约束就是说，生产1个桌子所需的资源的售卖收益，要大于生产1个桌子的销售收益。第二条约束，生产1个椅子所需的资源售卖收益，要大于生产1个椅子的销售收益，约束条件的目标就是要求不吃亏。目标函数是希望资源出售的总价最低，目标就是满足市场竞争性原则。

那么王老板按照资源出租模型（对偶规划问题），求解就可以获得其出租木工、油漆工资源的价格，这样既能保证不吃亏（出租资源的租金收入并不低于自己生产时的销售收入），又是的出租价格对李老板有极大的吸引力（李老板所付出的总租金W最少）。本质上，是一种“共赢”。

2.获得线性规划的对偶(Finding the Dual of an LP)

给定一个线性规划原问题，如何写出其对偶问题呢？这里我们介绍两种情况下的变换方式：（1）对称型对偶问题；（2）非对称型对偶问题

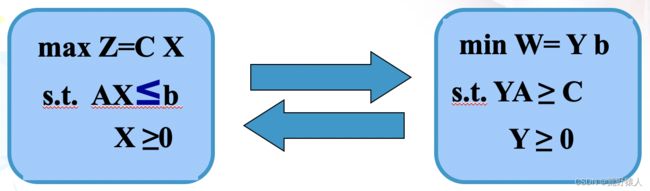
2.1 对称型对偶问题

如果原问题如下：

那么其对偶问题为： 

 其中称为对偶变量。上述对偶问题称为：对称型对偶问题。原问题记为（P），对偶问题简记为（D），称问题（P）和（D）为一对对偶问题。

对称型对偶问题的对偶规则如下（重要！！！）：

1. 给每个原始约束条件定义一个非负对偶变量，； 

2. 使原问题的目标函数系数变为其对偶问题约束条件的右端项；

3. 使原问题约束条件的右端项常数变为其对偶问题目标函数的系数；

4.将原问题约束条件的系数矩阵转置，得到其对偶问题约束条件的系数矩阵；

5.改变约束问题不等号的方向，即将“”改为“”;

6.原问题为“max”型，对偶问题为“min”型。

一个例子：

                      

                         原问题                                                              对偶问题

2.2 非对称型对偶问题

如果原问题不是对称型问题，那么就是非对称型问题。非对称问题的对偶规则如下

（重要！！！）：

 1. 原问题为“max”，对偶问题为“min”;

2. 原问题中目标函数系数变为其对偶问题约束条件的右端项常数；

3. 原味题约束条件的右端项常数变为其对偶问题目标函数的系数；

4. 原问题约束条件的系数矩阵转置，即为其对偶问题的系数矩阵；

5. 原问题的变量个数等于其对偶问题的约束条件个数，原问题约束条件个数等于其对偶问题变量的个数；

6. 在求极大值的原问题中，“”， “”和“”的约束条件分别对应其对偶变量“”，“”和“无符号限制”；

7. 在求极大值的原问题中，变量“”，“”和“无符号限制”分别对应其对偶约束条件中“”，“”和“”约束。

 一个重要的例子！

3.对偶定理(The Dual Theorem)

我们以对称型对偶问题为例（非对称型问题可以转化为对称型问题），来讲解对偶定理。

                                  原问题                                                                对偶问题

这两个问题的矩阵表达如下：

                                                

                               原问题                                                                对偶问题

性质1: 对称性定理： 对偶问题的对偶是原问题

3.1 弱对偶定理 

性质2 弱对偶原理(弱对偶性)：设和分别是问题(P)和(D)的可行解，则必有

，即：

---

证明：当和为原问题(P)和对偶问题(D)的一个可行解，有

,  和

对第一个式子左乘，第二个式子右乘，得到

，和

于是我们有

 证毕。

推论1：原问题任一可行解的目标函数值是其对偶问题目标函数值的下界；反之，对偶问题任一可行解的目标函数值是其原问题目标函数值的上界。

推论2：在一对对偶问题（P）和（D）中，若其中一个问题可行但目标函数无界，则另一个问题无可行解；反之不成立。这也是对偶问题的无界性。

若（P）为无界解，则（D）无可行解；

若（D）为无界解，则（P）无可行解；

推论3：在一对对偶问题（P）和（D）中，若一个可行（如P），而另外一个不可行（如D），则该可行的问题目标函数值无界。

3.2 最优性定理 

性质3 最优性定理：如果是原问题的可行解，是对偶问题的可行解，并且：

，即：z = w

则是原问题的最优解，是其对偶问题的最优解。

3.3 强对偶定理 

性质4 强对偶性：若原问题及其对偶问题均具有可行解，则两者均具有最优解，且他们最优解的目标函数值相等。

---

证明：

 注意：原始单纯形的最终表，检验数均要求0， 这里我们令（假设），根据原始单纯形表中检验数0，我们知道

继续往后推，既可以得到最终原问题与对偶问题均具有可行解，那么两者均具有最优解，且他们最优解的目标函数值相等。

推论1：若一对对偶问题中的任意一个有最优解，则另外一个也有最优解，且目标函数最优值相等；若一个问题无最优解，则另一个问题也无最优解。一对对偶问题的关系，有且仅有下列三种：

1. 都有最优解，且目标函数最优值相等；
2. 两个都无可行解；
3. 一个问题无界，则另一个问题无可行解。

4.互补松弛定理(Complementary Slackness) 

性质5 互补松弛性：设和分别是问题和问题的可行解，则他们分别是最优解的充要条件是：

其中：、为松弛变量。

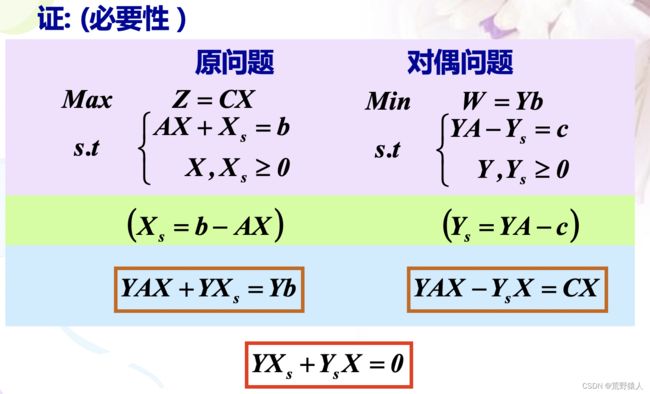
证明：(必要性，即如果和分别是问题和问题的可行解且是最优解，那么有互补松弛条件)

解释：在线性规划问题的最优解中，若对应某一约束条件的对偶变量值为非零，则该约束条件取严格等式；另外一方面，如果约束条件取严格不等式，则其对应的对偶变量一定为零。（重要！！！）

紧约束与松约束

一个约束称为“紧约束”，如果该约束在所有最优解上的值使左右取等号。即我们把严格等式约束称为紧约束（或起作用约束）。

一个约束称为“松约束”，不是紧约束的约束称为松约束，即把某一最优解处取严格不等式的约束称为松约束（或不起作用约束）。

松紧关系

对于最优解和而言，松约束的对偶约束是紧约束。

参考例题（互补松弛关系的应用：在已知一个问题的最优解时，求解另外一个问题的最优解）

5.影子价格(Shadow Prices)

原问题变量与参数的经济学解释如下： 

 对偶问题变量与参数的经济学解释如下：

 

 

 ​​​​​ 

 

6.对偶单纯形法(The Dual Simplex Method)

6.1 对偶单纯形法的由来

6.2 对偶单纯形法的步骤

对于最大化问题（使用row0形式的单纯形表）

Step 1： 是否每个约束的右端项都是非负？如果是的话，最优解已经被找到。如果不是，那么至少有一个约束的右端项是负数，然后进入Step 2；

Step 2：选择最小负值对应的基变量出基。为了选择入基变量，对于哪些具有非负系数的非基变量，我们计算Row0与系数的比值，其中最小正比值对应的非基变量入基。这种形式的比值保证了对偶可行。然后使用初等行变换进行出基和入基操作；

Step 3: 如果还有右端项为非负的约束并且该约束每个系数全都非负，那么LP问题无可行解。如果没有发现不可行，那么返回Step 1.

6.3 对偶单纯形法的三种用途

（1）当一个约束加入到LP中时，找到新的最优解；

主要有以下三种情况可能会发生 

• 当前最优解满足新约束，那么当前解仍然是最优的。
• 当前解不满足新约束，但是LP仍然有可行解，此时可以用对偶单纯形法来确定新的最优解
• 额外的约束值得LP问题没有可行解。

（2）当改变LP的右端项系数时，找到新的最优解；

如果右端项系数改变且当前最优基变得不可行，那么对偶单纯形法可以被用来寻找新的最优解。

（3）求解标准化的最小化问题；

可以简化求解过程，避免使用大M法和两阶段法获得初始解。

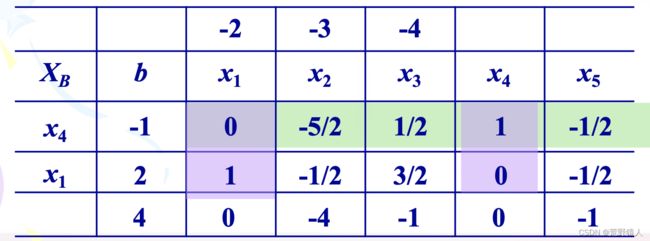
6.4 对偶单纯形法的求解案例

对偶单纯形法的第三种用途：求解标准化的最小化问题。 

 

 主要参考资料：中国矿业大学，运筹学课件