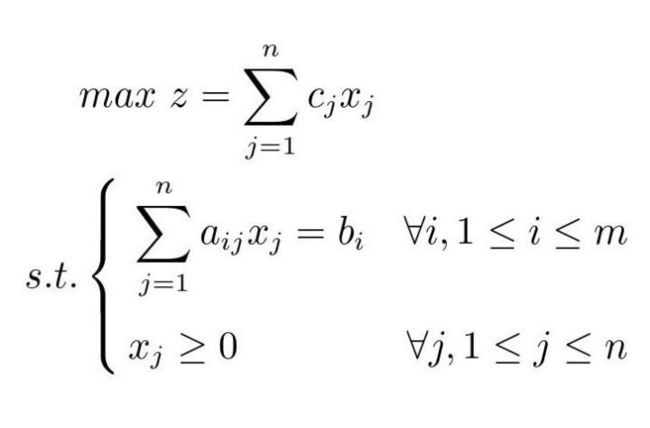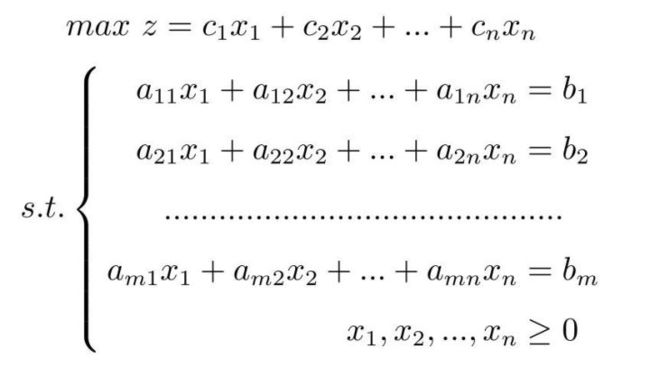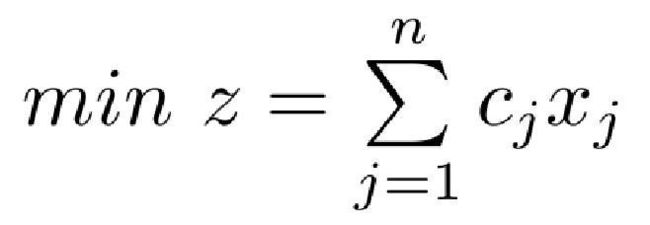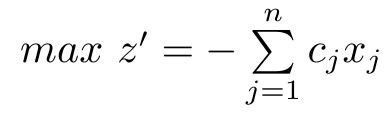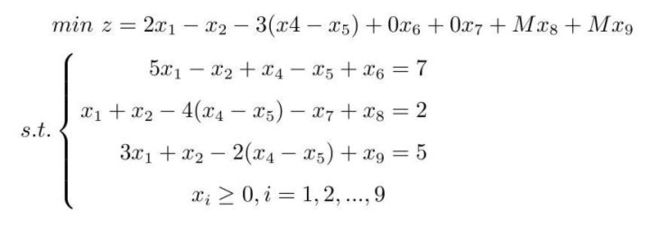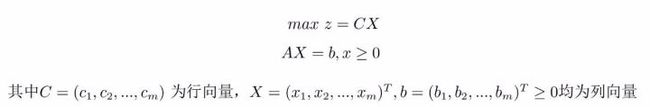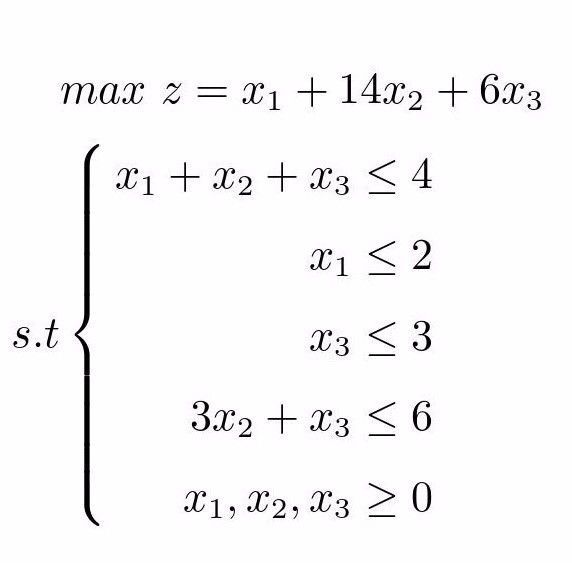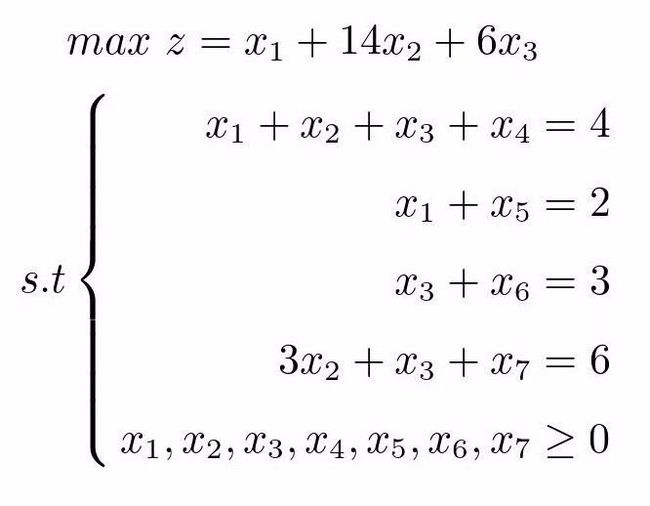单纯形法步骤
原文地址:快速掌握单纯形法
一、标准型
1)目标函数统一为求极大值(或极小值);
2)所有约束条件(除变量的非负条件外)必须都是等式,约束条件右端常数项(right-hand-side)b_i必须全为非负值;
3)所有变量的取值必须全为非负值。
下面模型即为标准形式的展开型:
二、转化
线性规划问题往往并非标准形式。
这个过程包括四个部分的转换:
1. 目标函数的转换:
统一求极大值,若是求极小值,则可将下面的式子乘以(-1)。即:
转化为:
2. 变量的转换:
(1)对于已经是大于等于零的变量 x_j ≥ 0 不做变化;
(2)对于小于等于零的变量 x_j,取负号令其变为大于等于零的变量,即若 x_j ≤ 0,则 定义新变量x_j' = -x_j,x_j' ≥ 0;
(3)若 x_j 取值无约束,可令两个新的非负变量x_j', x_j'', 然后用x_j = x_j' - x_j''替换原问题中的x_j。
3. 约束条件的右端项常数的转换:
b_i < 0 时,只需将等式或不等式两端同乘(-1);
4. 约束条件的转换:
将所有不等式全部转换为等式:
对于“≤ ”型约束加入一个变量 x_s,x_s ≥ 0;
对于“≥ ”型约束则减去一个变量 x_s,x_s ≥ 0。
加到原约束条件中的变量,称为松弛变量,在实际问题中它表示未被充分利用的资源或缺少的资源,所以在引入模型后它们在目标函数中的系数均为零。
为了构造出初始基变量,约束条件还可能需要加上人工变量。人工变量最终必须等于0才能保持原问题性质不变。为保证人工变量为0,在目标函数中令其系数为M。M为无限大的正数,这是一个惩罚项,倘若人工变量不为零,则目标函数就永远达不到最优,所以必须将人工变量逐步从基变量中替换出去。如若到最终表中人工变量仍没有置换出去,那么这个问题就没有可行解,当然亦无最优解。
替换后的结果:
注:x_4, x_5是将自由变量x_3转化为非负变量而引入的新变量,x_6, x_7是松弛变量,x_8, x_9是人工变量。
三、矩阵式
矩阵A如下式:
A为m×n矩阵。假设A的秩为m,即假设不存在冗余的约束条件,则m>n(应该是<?)时,因为方程数量比变量数目多,必定有多个可行解,即可利用单纯形法来计算最优解。
四、单纯形法的算法步骤
1. 确定初始可行基和初始基可行解,
建立初始单纯形表;
2. 最优性检验 若在当前表的目标函数对应的行中,所有非基变量的系数非正,则可判断得到最优解(目标值不会再继续增大,不会出现更优解),可停止计算。否则转入下一步;
3. 若单纯形表中1至m列构成单位矩阵,在j=m+1至n列中,若有某个对应x_k的系数列向量 P_k ≤ 0,则此问题是无界,停止计算。否则,转入下一步;
4. 挑选目标函数对应行中系数最大的非基变量作为进基变量。假设x_k为进基变量,按θ规则[1]计算,可确定x_l为出基变量,转下一步;
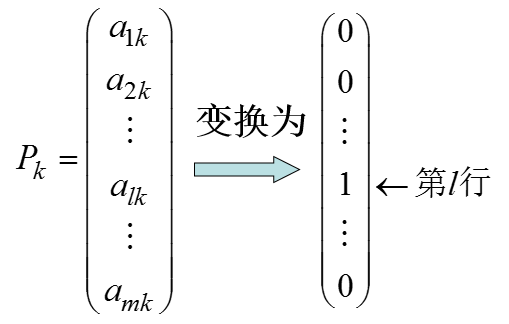
5. 以a_lk为主元素进行迭代(即用高斯消去法或称为旋转运算),把x_k所对应的列向量进行变换[2];
6. 重复2-5步,直到所有检验数非正后终止,得到最优解。
[1] θ规则
其中b_i是当前表中的右手项,a_ik即为在第i个约束中变量k的系数。(找最小值,防止待进基的变量值过大使得出基变量量为负)
[2] x_k列变换
五、例子
对于线性规划问题:
加入松弛变量,转化为标准形式得:
于是我们可以构造单纯形表,其中最后一行有星号的列为基变量。初始基可行解为(x_4, x_5, x_6, x_7)。
在单纯形表中,我们发现非基变量x的系数大于零,因此可以通过增加这些x的值,来使目标函数增加。
上表中c_2最大,因此我们选择x_2作为新的基变量。按照θ规则,x_7出基。通过高斯变换得到的新的单纯形表为:
继续计算,我们得到:
此时我们发现,所有非基变量的系数全部非正,即增大任何基变量的值并不能使得目标函数增大。于是我们可以断定该问题的最优解是z = 32, X = (0, 1, 3, 0, 2, 0, 0).