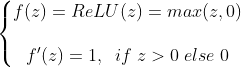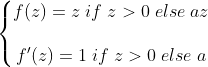神经网络基础2：激活函数

不是所有信息都是有用的，一些只是噪音；激活函数可以帮助神经网络做这种隔离，激活有用的信息，并抑制无关的数据点。

以下将介绍神经网络中常用的几种激活函数：sigmoid、tanh、ReLu、leaky ReLu、PReLu、ELU、maxout、softmax，以及它们各自的特性。

记激活函数的输入z为上一层输出的线性组合，输入Z为上一层输出的多组不同的线性组合（vector）。

sigmoid

sigmoid函数是一个平滑函数，并且具有连续性和可微性；其输出值在(0,1)之间，可当做概率使用，可用于二分类模型输出层的激活函数；随着abs(z)越来越大，梯度会越来越小，在abs(z)>5之后梯度就基本接近0了；越是接近sigmoid的两端，相对z的改变，f(z)就越趋向于作出非常小的反应；sigmoid函数在其大部分定义域内都饱和，在这些饱和区域内梯度会很小或者消失了（由于值极小，无法做出显著的改变了），网络拒绝进一步学习，或者学习速度剧烈地变慢了，这种现象称之为梯度消失，当网络较深时(链式法则，导数累乘)，这种现象会越加明显；但是反过来，sigmoid的饱和特性能够让其对输入变化或噪声更鲁棒。

另一个问题，sigmoid函数的输出在(0,1)之间，都是正数，不是zero-centered的，这会拖慢学习的收敛速度（原因可以参看上一篇https://blog.csdn.net/yeqiustu/article/details/106172592）。

还有一个问题就是sigmoid函数涉及幂运算，计算量较大。

tanh

可以看到tanh函数是对sigmoid函数的拉伸与偏移，输出是zero-centered的；然而，gradient vanishing的问题（饱和区比sigmoid更大）和幂运算的问题仍然存在。

ReLU

Rectified Linear Units，线性整流单元

可以看到，当z<0时，ReLU硬饱和，梯度为0；而当z>0时，则梯度为1；所以，ReLU 能够在z>0时保持梯度不衰减，从而缓解梯度消失问题，收敛速度远快于sigmoid和tanh；激活部分神经元，增加稀疏性；而且计算速度非常快，只需要判断输入是否大于0；

当输入落入硬饱和区时，对应权重无法更新，这种现象被称为Dead ReLU Problem--“神经元死亡”，当网络中很多神经元都处于死亡状态，则网络会训练不动；有两个主要原因可能导致这种情况产生: (1) 非常不幸的参数初始化，这种情况比较少见 (2) learning rate太高导致在训练过程中参数更新太大，不幸使网络进入这种状态。解决方法是可以采用Xavier初始化方法，以及避免将learning rate设置太大或使用adagrad等自动调节learning rate的算法。

另外，ReLU的输出不是zero-centered（可通过BN等手段解决）。

尽管存在这两个问题，ReLU目前仍是最常用的激活函数，在搭建人工神经网络的时候推荐优先尝试！

ReLU的变形

为了解决Dead ReLU Problem和缓解ReLU非zero-centered的问题，出现了一些ReLU的变形，即对负数硬饱和区进行修改，使这区域的输出为负和梯度不再为0；

Leaky ReLU与Parametric ReLU

Leaky ReLU将a作为人工设定的超参，而Parametric ReLU则将a当做一个可学习的参数。

Exponential Linear Units，ELU

ELU在左侧使用指数函数，具有软饱和性，对输入变化或噪声更鲁棒。

这些变形理论上虽然好于ReLU，但在实际使用中目前并没有好的证据表明它们总是优于ReLU。

高斯误差线性单元（GELU）

高斯误差线性单元激活函数在最近的 Transformer 模型（谷歌的 BERT 和 OpenAI 的 GPT-2）中得到了应用。不怎么理解，先记录下来，有时间再看下论文（https://arxiv.org/pdf/1606.08415.pdf）研究下。

maxout

主要用来对多组feature map进行筛选，只保留最显著的单元，抑制小值单元（无关或不重要），减少干扰；常见于CV任务中。

softmax

其中取指数，第一个原因是要模拟 max 的行为，所以要让大的更大；第二个原因是需要一个可导的函数。

每个输出值都在0-1之间，和为1，可作为概率分布，主要用于多分类任务的输出层；

当K=2时，softmax有2组参数W1、W2，而sigmoid只要一组参数W，参数有冗余，化简后与sigmoid等价；