【动手学深度学习v2李沐】学习笔记04:Softmax回归、损失函数、图片分类数据集、详细代码实现
前文回顾:线性回归、基础优化算法、线性回归实现
文章目录
- 一、Softmax回归
-
- 1.1 多类分类
-
- 1.1.1 回归 vs 分类
- 1.1.2 均方损失
- 1.2 校验比例
- 1.3 Softmax和交叉熵损失
- 1.4 总结
- 二、损失函数
-
- 2.1 均方损失 L2 Loss
- 2.2 绝对值损失 L1 Loss
- 2.3 哈珀鲁棒损失 Huber's Robust Loss
- 三、图片分类数据集
-
- 3.1 获取数据集
- 3.2 查看数据集
- 3.3 读取小批量数据
- 3.4 封装
- 四、Softmax回归从零开始实现
-
- 4.1 数据集和网络参数
- 4.2 构造
-
- 4.2.1 Softmax模型
- 4.2.2 交叉熵损失函数
- 4.2.3 小批量随机梯度下降
- 4.3 验证
-
- 4.3.1 计算预测正确的数量
- 4.3.2 评估准确率
- 4.4 训练
-
- 4.4.1 一个epoch的训练
- 4.4.2 训练总过程
- 4.5 预测
- 五、Softmax回归简洁实现
-
- 5.1 数据集
- 5.2 构造
- 5.3 训练
一、Softmax回归
1.1 多类分类
1.1.1 回归 vs 分类
虽然Softmax回归的名字里面有回归,但它其实是个分类问题。
- 回归:估计一个连续值
- 分类:预测一个离散类别
| 回归 | 分类 |
|---|---|
| 单连续数值输出 自然区间 R R R 跟真实值的区别作为损失 |
通常多个输出 输出i是预测为第i类的置信度 |
 |
 |
1.1.2 均方损失
我们首先对类别进行一位有效编码(对于n分类,输出值共有n个元素,其中1个预测值为1,其余n-1个值为0):
y ⃗ = [ y 1 y 2 ⋯ y n ] T y i = { 1 i = y 0 o t h e r w i s e \vec{y}=\begin{bmatrix}y_1 & y_2 & \cdots & y_n\end{bmatrix}^T \qquad y_i=\begin{cases}1\quad i=y \\ 0 \quad otherwise\end{cases} y=[y1y2⋯yn]Tyi={1i=y0otherwise之后,我们可以使用最简单的均方损失训练,但后面会介绍更好用的损失。
我们采用具有最大值的类别作为预测的类别:
y ^ = a r g m a x i o i \hat{y}=\mathop{argmax}\limits_i \; o_i y^=iargmaxoi对于分类问题,我们不关心预测出来的具体值是多少,而更关心对正确类别的置信度是不是足够的大。我们需要更置信地识别正确类,即正确类的预测值要有较大的余量。
也就是说,我们期望对正确类别的预测值 o y o_y oy与对错误类别的预测值 o i o_i oi有足够大的差距,即:
o y − o i ≥ Δ ( y , i ) o_y-o_i \geq \Delta(y, i) oy−oi≥Δ(y,i)
1.2 校验比例
我们希望预测的结果是:输出匹配概率(为各种类别的概率)。这需要使我们在各类别上预测出的值均为非负值,且这些值的和为1。
我们暂时先以softmax()作为预测过程,则通过输入值 o ⃗ \vec{o} o得到预测值 y ⃗ ^ \hat{\vec{y}} y^的过程可以表示为:
y ⃗ ^ = s o f t m a x ( o ⃗ ) \hat{\vec{y}}=softmax(\vec{o}) y^=softmax(o)
为了使输出的值满足输出匹配概率的条件(非负,和为1),我们对之前预测出的值 y ⃗ ^ \hat{\vec{y}} y^中的每一个元素 y i ^ \hat{y_i} yi^做如下变换:
y i ^ = e o i ∑ k e o k \hat{y_i}=\frac{e^{o_i}}{\sum_ke^{o_k}} yi^=∑keokeoi
多分类问题的真实结果 y ⃗ \vec{y} y也可以看做是一组概率(正确类别的概率为1,错误类别的概率为0)。因此,我们可以将真实概率 y ⃗ \vec{y} y和预测概率 y ⃗ ^ \hat{\vec{y}} y^的区别作为损失值。
1.3 Softmax和交叉熵损失
在上一小节中,我们已经将预测出的值转化成了一组概率,并决定以真实概率与预测概率的区别来衡量损失。
而交叉熵常用来衡量两个概率的区别,因此,我们将它作为损失:
l ( y ⃗ , y ⃗ ^ ) = − ∑ i y i log y i ^ = − log y ^ y l(\vec{y}, \hat{\vec{y}})=-\sum\limits_i y_i\log{\hat{y_i}}=-\log{\hat{y}_y} l(y,y^)=−i∑yilogyi^=−logy^y该损失的梯度是真实概率和预测概率的区别:
∂ o i l ( y ⃗ , y ⃗ ^ ) = s o f t m a x ( o ⃗ ) i − y i \partial _{o_i}l(\vec{y}, \hat{\vec{y}})=softmax(\vec{o})_i-y_i ∂oil(y,y^)=softmax(o)i−yi
1.4 总结
- Softmax回归是一个多类分类模型。
- 使用Softmax操作子得到每个类的预测置信度。
- 使用交叉熵来衡量预测和标签的区别。
二、损失函数
这一节,我们将介绍三个常用的损失函数。
2.1 均方损失 L2 Loss
定义:
l ( y , y ′ ) = 1 2 ( y − y ′ ) 2 l(y, y')=\frac{1}{2}(y-y')^2 l(y,y′)=21(y−y′)2
特性:
- 似然函数为高斯分布。
- 梯度为一次函数,穿过原点。
- 当预测值距离真实值比较远时,梯度会比较大,参数更新的幅度会比较大。当预测值距离真实值越来越近时,梯度逐渐变小,参数更新的幅度也逐渐变小。
- 但有些时候,我们在预测值离原点远的时候,并不希望有那么大的更新幅度。
2.2 绝对值损失 L1 Loss
定义:
l ( y , y ′ ) = ∣ y − y ′ ∣ l(y, y')=|y-y'| l(y,y′)=∣y−y′∣
特性:
- 其导数为:
d L 1 ( w ) d w = { 1 w > 0 0 w < 0 \frac{dL_1(w)}{dw}= \begin{cases}1 \qquad w>0 \\ 0 \qquad w<0\end{cases} dwdL1(w)={1w>00w<0 - 即使预测值离原点很远,梯度也一直是个常量。
- 缺点是在原点处不可导,并且会有从1到-1的剧烈变化,不平滑性可能会导致在预测的后期不够稳定。
2.3 哈珀鲁棒损失 Huber’s Robust Loss
定义:
l ( y , y ′ ) = { ∣ y − y ′ ∣ − 1 2 ∣ y − y ′ ∣ > 1 1 2 ( y − y ′ ) 2 o t h e r w i s e l(y, y')=\begin{cases}|y-y'|-\frac{1}{2} \qquad |y-y'|>1 \\ \frac{1}{2}(y-y')^2 \qquad \; \; \;otherwise\end{cases} l(y,y′)={∣y−y′∣−21∣y−y′∣>121(y−y′)2otherwise
特性:
- 结合了L1 Loss和L2 Loss的优点,规避了缺点。
- 梯度在预测值大于1或者小于-1的时候为常数,在-1和1之间是渐变的。
- 在预测值离原点很远的时候,梯度值保持常数。
- 在预测值接近原点的时候,梯度值逐渐减小,保证优化是比较平滑的。
三、图片分类数据集
MNIST数据集是图像分类中广泛使用的数据集之一,但作为基准数据集过于简单。我们将使用类似但更复杂的Fashion-MNIST数据集。
3.1 获取数据集
我们使用了如下的库。本文中代码针对PyCharm,并做了部分修改。
from matplotlib import pyplot as plt
import torch
import torchvision
from torch.utils import data
from torchvision import transforms
from d2l import torch as d2l
d2l.use_svg_display()
通过框架中的内置函数将Fashion-MNIST数据集下载并读取到内存中。其中,train=参数指定该数据为训练集还是测试集,transform=参数指定要对数据进行的操作。
# 下载数据集 并读到内存中
# 通过ToTensor实例将图像数据从PIL类型变换成32位浮点数格式
# 并除以255使得所有像素的数值均在0到1之间
trans = transforms.ToTensor()
mnist_train = torchvision.datasets.FashionMNIST(root="../data", train=True,
transform=trans, download=True)
mnist_test = torchvision.datasets.FashionMNIST(root="../data", train=False,
transform=trans, download=True)
print(len(mnist_train), len(mnist_test))
print(mnist_train[0][0].shape)
3.2 查看数据集
由于Fashion-MNIST数据集中全是裤子、靴子、包等物品的图片,我们使用两个可视化数据集的函数,以此,对预测的结果进行展示。
def get_fashion_mnist_labels(labels):
""" 返回Fashion-MNIST数据集的文本标签 """
text_labels = ['t-shirt', 'trouser', 'pullover', 'dress', 'coat',
'sandal', 'sheet', 'sneaker', 'bag', 'ankle boot']
return [text_labels[int(i)] for i in labels]
def show_images(imgs, num_rows, num_cols, titles=None, scale=1.5):
""" Plot a list of images. """
figsize = (num_cols * scale, num_cols * scale)
_, axes = d2l.plt.subplots(num_rows, num_cols, figsize=figsize)
axes = axes.flatten()
for i, (ax, img) in enumerate(zip(axes, imgs)):
if torch.is_tensor(img):
# 图片张量
ax.imshow(img.numpy())
else:
# PIL图片
ax.imshow(img)
ax.set_title(titles[i])
我们可以使用上述函数来展示几张图片及其对应的标签。
这里,我们先用DataLoader()函数处理数据集,之后用iter()方法将数据集转换为迭代器格式,再用next()方法取出第一个小批量。
# 几个样本的图像及其相应的标签
X, y = next(iter(data.DataLoader(mnist_train, batch_size=18)))
show_images(X.reshape(18, 28, 28), 2, 9, titles=get_fashion_mnist_labels(y))
plt.show()
3.3 读取小批量数据
我们先来读取一个小批量,大小为batch_size
batch_size = 256
def get_dataloader_workers():
""" 使用4个进程来读取的数据 """
return 4
train_iter = data.DataLoader(mnist_train, batch_size, shuffle=True,
num_workers=get_dataloader_workers())
timer = d2l.Timer()
for X, y in train_iter:
continue
print(f'{timer.stop():.2f} sec')
若此处出现报错:RuntimeError: DataLoader worker (pid(s) 9288) exited unexpectedly 或者其他类似报错
我们可以将get_dataloader_workers()中的return 4修改为return 0。
这是在使用多进程读取数据时报的错,我们要根据电脑的CPU选择合适的进程数,或者直接选0。
3.4 封装
最后,我们将对数据集的下载和加载封装成一个函数,方便日后使用。
def load_data_fashion_mnist(batch_size, resize=None):
""" 下载Fashion-MNIST数据集,然后将其加载到内存中 """
trans = [transforms.ToTensor()]
if resize:
trans.insert(0, transforms.Resize(resize))
trans = transforms.Compose(trans)
mnist_train = torchvision.datasets.FashionMNIST(root="../data", train=True,
transform=trans, download=True)
mnist_test = torchvision.datasets.FashionMNIST(root="../data", train=False,
transform=trans, download=True)
return (data.DataLoader(mnist_train, batch_size, shuffle=True,
num_workers=get_dataloader_workers()),
data.DataLoader(mnist_test, batch_size, shuffle=True,
num_workers=get_dataloader_workers()))
四、Softmax回归从零开始实现
4.1 数据集和网络参数
我们直接使用上一节中定义的函数来加载数据集,并设置批量大小batch_size为256.
import torch
from IPython import display
from d2l import torch as d2l
batch_size = 256
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size)
Fashion-MNIST中的数据类型为 28 × 28 × 1 28 \times 28 \times 1 28×28×1,我们需要将其转换为长度为784的一维向量。因为我们的数据集有10个类别,所以网络输出维度为10,。
# 展平图像
num_inputs = 784
num_outputs = 10
W = torch.normal(0, 0.01, size=(num_inputs, num_outputs), requires_grad=True)
b = torch.zeros(num_outputs, requires_grad=True)
4.2 构造
4.2.1 Softmax模型
回顾: 给定一个矩阵,可以对所有元素求和
X = torch.tensor([[1.0, 2.0, 3.0], [4.0, 5.0, 6.0]]) print(X.sum(0, keepdim=True), X.sum(1, keepdim=True))
实现操作: 有了上述求和操作,我们就可以实现Softmax操作:
s o f t m a x ( X ) i j = e X i j ∑ k e X i k softmax(X)_{ij}=\frac{e^{X_{ij}}}{\sum_ke^{X_{ik}}} softmax(X)ij=∑keXikeXij
def softmax(X):
X_exp = torch.exp(X)
partition = X_exp.sum(1, keepdim=True)
return X_exp / partition # 这里应用了广播机制
实现模型: 接下来我们使用softmax操作实现softmax模型。
def net(X):
return softmax(torch.matmul(X.reshape(-1, W.shape[0]), W) + b)
4.2.2 交叉熵损失函数
回顾: 利用python的花式索引,取得样本对应的预测值。
我们创建一个数据y_hat,其中包含2个样本在3个类别中的预测概率,使用y作为y_hat中概率的索引。# 举个例子 y = torch.tensor([0, 2]) y_hat = torch.tensor([[0.1, 0.3, 0.6], [0.3, 0.2, 0.5]]) print(y_hat[[0, 1], y])上例中我们最后取到了
y_hat[0][0]和y_hat[1][2]两个值。
通过上述花式索引,我们可以实现交叉熵损失函数:
def cross_entropy(y_hat, y):
return -torch.log(y_hat[range(len(y_hat)), y])
# 实现交叉熵损失函数
print(cross_entropy(y_hat, y))
在上述代码中,我们首先通过y_hat[range(len(y_hat)), y]取得了y_hat[0][y[0]]、y_hat[1][y[1]]、…y_hat[n][y[n]]这一系列预测值。之后,通过-torch.log()对这些预测值取负对数,从而计算得到了交叉熵。
4.2.3 小批量随机梯度下降
我们使用小批量随机梯度下降来优化模型的损失函数。
lr = 0.1
def updater(batch_size):
return d2l.sgd([W, b], lr, batch_size)
4.3 验证
4.3.1 计算预测正确的数量
将预测类别与真实y元素进行比较。
def accuracy(y_hat, y):
""" 计算预测正确的数量 """
if len(y_hat.shape) > 1 and y_hat.shape[1] > 1:
y_hat = y_hat.argmax(axis=1) # 将每一行预测值最大的下标存储到y_hat中
cmp = y_hat.type(y.dtype) == y
return float(cmp.type(y.dtype).sum())
# 将预测类别与真实y元素进行比较
print(accuracy(y_hat, y) / len(y)) # 输出预测正确的概率
4.3.2 评估准确率
我们可以评估在任意模型net的准确率:
def evaluate_accuracy(net, data_iter):
""" 计算在指定数据集上模型的精度 """
if isinstance(net, torch.nn.Module):
net.eval() # 将模型设置为评估模式,即不计算梯度
metric = d2l.Accumulator(2) # 正确预测数、预测总数
for X, y in data_iter:
metric.add(accuracy(net(X), y), y.numel())
return metric[0] / metric[1]
上述代码中,我们通过eval()将模型设置为评估模式,即:不更新参数。metric为一维向量,含有两个元素。其中,metric[0]为预测正确的数量,metric[1]为进行预测的总数。最后,通过metric[0] / metric[1]计算得到预测精度。
4.4 训练
4.4.1 一个epoch的训练
我们将训练过程封装起来,方便以后重用。
# Softmax回归的训练
def train_epoch_ch3(net, train_iter, loss, updater):
if isinstance(net, torch.nn.Module):
net.train() # 开启训练模式
metric = d2l.Accumulator(3)
for X, y in train_iter:
y_hat = net(X)
l = loss(y_hat, y)
if isinstance(updater, torch.optim.Optimizer): # 用框架中的模型实现
updater.zero_grad()
l.backward()
updater.step()
metric.add(float(1) * len(y),
accuracy(y_hat, y),
y.size().numel())
else: # 从零开始实现
l.sum().backward()
updater(X.shape[0])
metric.add(float(l.sum()),
accuracy(y_hat, y),
y.numel())
return metric[0] / metric[2], metric[1] / metric[2]
4.4.2 训练总过程
接下来,我们综合训练和验证,封装成如下的总的网络训练代码:
def train_ch3(net, train_iter, test_iter, loss, num_epochs, updater):
# 可视化
animator = d2l.Animator(xlabel='epoch', xlim=[1, num_epochs], ylim=[0.3, 0.9],
legend=['train loss', 'train acc', 'test acc'])
for epoch in range(num_epochs):
train_metrics = train_epoch_ch3(net, train_iter, loss, updater)
test_acc = evaluate_accuracy(net, test_iter)
animator.add(epoch+1, train_metrics + (test_acc, ))
train_loss, train_acc = train_metrics
d2l.plt.show()
assert train_loss < 0.5, train_loss
assert train_acc <= 1 and train_acc > 0.7, train_acc
assert test_acc <= 1 and test_acc > 0.7, test_acc
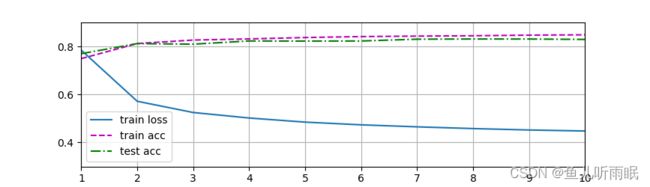
我们训练模型10个迭代周期。
# 训练模型10个迭代周期
num_epochs = 10
train_ch3(net, train_iter, test_iter, cross_entropy, num_epochs, updater)
4.5 预测
我们使用训练好的模型,对测试集中的部分数据进行预测。
def predict_ch3(net, test_iter, n = 6):
""" 预测标签 """
for X, y in test_iter:
break
trues = d2l.get_fashion_mnist_labels(y)
preds = d2l.get_fashion_mnist_labels(net(X).argmax(axis=1))
titles = [true + '\n' + pred for true, pred in zip(trues, preds)]
d2l.show_images(X[0:n].reshape((n, 28, 28)), 1, n, titles=titles[0:n])
d2l.plt.show()
# 对图像进行分类预测
predict_ch3(net, test_iter)
五、Softmax回归简洁实现
5.1 数据集
通过深度学习框架的高级API能够使实现softmax回归变得更加容易。
import torch
from torch import nn
from d2l import torch as d2l
batch_size = 256
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size)
5.2 构造
实现网络模型:
Softmax回归的输出层是一个全连接层。由于PyTorch不会显式地调整输入的形状,所以,我们首先用一个展平层(flatten) 在线性层前调整网络输入的形状。
def init_weights(m):
if type(m) == nn.Linear:
nn.init.normal_(m.weight, std=0.01)
net = nn.Sequential(nn.Flatten(), nn.Linear(784, 10))
net.apply(init_weights)
上述代码中,我们构造了一个初始化权重的方法。当输入的类型为Linear时,会将权重重置为方差为0.01的正态函数值。
实现损失函数:
在交叉熵损失函数中传递未归一化的预测,并同时计算softmax及其对数。
# 交叉熵损失函数
loss = nn.CrossEntropyLoss(reduction='none')
注意:
如果后面绘图时没有蓝色的loss曲线,则这里一定要指明参数reduction='none'。
实现优化算法:
使用学习率为0.1的小批量随机梯度下降作为优化算法。
# 使用学习率为0.1的小批量随机梯度下降作为优化算法
trainer = torch.optim.SGD(net.parameters(), lr=0.1)
5.3 训练
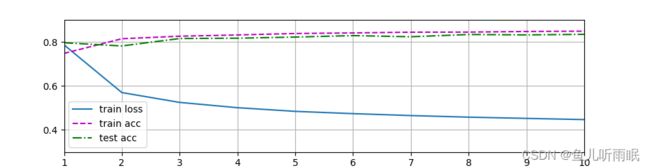
调用之前定义的训练函数来训练模型
# 训练模型
num_epochs = 10
d2l.train_ch3(net, train_iter, test_iter, loss, num_epochs, trainer)