KNN算法(附鸢尾花分类实现)
1.k近邻算法
k近邻学习(K-Nearest Neighbor,简称KNN)学习是一种常用的监督学习方法,其工作机制非常简单:给定测试样本,基于某种距离度量找出训练集中与其距离最近的k个样本,然后通过这k个邻居样本来进行预测,那种类别的邻居数量多,这个测试样本就被认为是那个类别的。与“投票”较为类似。下图是一个KNN的二分类问题的一个实列,可以看出k的取值不同,测试样本的分类也会不同,但都是基于他的邻居的投票的出的。
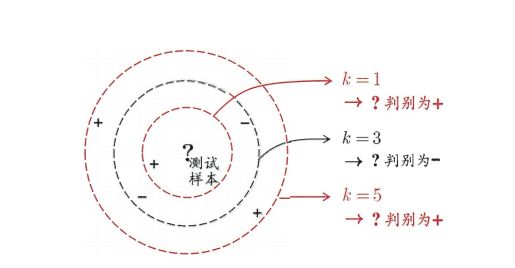
下面给出KNN算法的步骤:
① 计算未知样本与所有已知样本实列的距离。
②对距离从小到大进行排序
③选择出最近的k个已知实列
④这k个实列邻居进行投票,哪一个类别的票数多就认为k是那个类别的
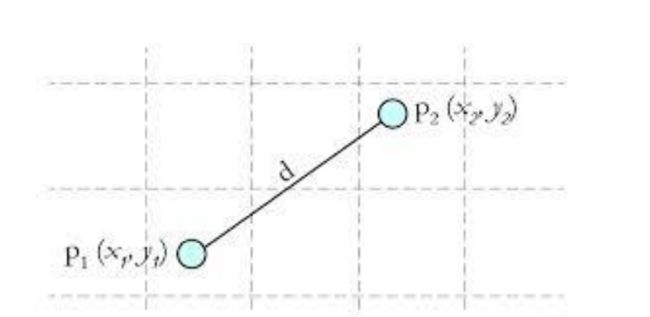
其中计算的距离一般为欧氏距离(欧几里得距离):
如图所示的欧几里得距离为: ( x 2 − x 1 ) 2 + ( y 2 − y 1 ) 2 \sqrt{(x_{2}-x_{1})^{2}+(y_{2}-y_{1})^{2}} (x2−x1)2+(y2−y1)2。
算法的缺点为:①算法复杂度较高,需要计算所有已知样本与要分类样本的距离。
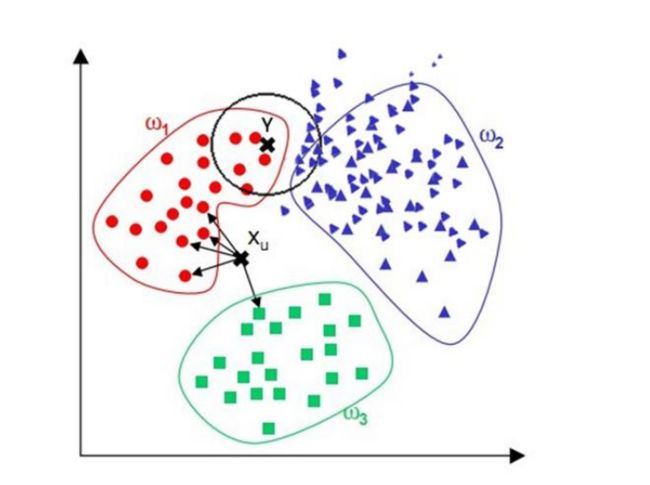
②当样本分布不平衡时,比如其中一类样本过大(实列数量过多)占主导时,新的未知实列容易被归类为这个主导样本,应为这类样本实列实列的数量过大,但这个新的未知实列实际并没有接近目标样本。如下图所示的黑色未知样本点,由于紫色的样本分布比红色样本分布更加密集,所以在分类时很容易将该未知样本分为了紫色类别,而通过观察显然应该被分为红色类别才合理一些。
2.KNN算法实现
import matplotlib.pyplot as plt
import numpy as np
import operator
# 已知分类的数据
x1 = np.array([3,2,1])
y1 = np.array([104,100,81])
x2 = np.array([101,99,98])
y2 = np.array([10,5,2])
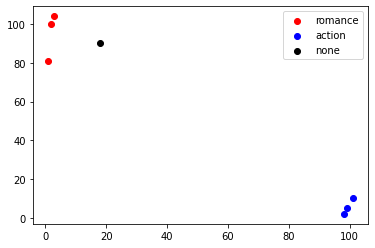
scatter1=plt.scatter(x1,y1,c='r')
scatter2=plt.scatter(x2,y2,c='b')
# 未知数据
x = np.array([18])
y = np.array([90])
scatter3 = plt.scatter(x,y,c='k')
plt.legend(handles=[scatter1,scatter2,scatter3],labels=['romance','action','none'],loc='best')
plt.show()
x_data=np.array([[3,104],
[2,100],
[1,81],
[101,10],
[99,5],
[81,2]])
y_data=np.array(['A','A','A','B','B','B'])
x_test=np.array([18,90])
np.tile(x_test,(x_data.shape[0],1))#复制test
array([[18, 90],
[18, 90],
[18, 90],
[18, 90],
[18, 90],
[18, 90]])
#计算x_data 与x_test的距离
distance=(((np.tile(x_test,(x_data.shape[0],1))-x_data)**2).sum(axis=1))**0.5
print(distance)
[ 20.51828453 18.86796226 19.23538406 115.27792503 117.41379817
108.2266141 ]
#从小到大排序
sotrdistance=distance.argsort()
sotrdistance
array([1, 2, 0, 5, 3, 4], dtype=int64)
classCount = {}
#设置k=5
k=5
for i in range(k):
label=y_data[sotrdistance[i]]#获取标签
classCount[label]=classCount.get(label,0)+1#统计标签数量
classCount
{'A': 3, 'B': 2}
# 根据operator.itemgetter(1)-第1个值对classCount排序,然后再取倒序
sotrclassCount=sorted(classCount.items(),key=operator.itemgetter(1), reverse=True)
sotrclassCount
[('A', 3), ('B', 2)]
#获取数量最多的标签
knn=sotrclassCount[0][0]
knn#所以x_test应属于A类别
'A'
sorted(iterable, cmp=None, key=None, reverse=False)
iterable – 可迭代对象。
cmp – 比较的函数,这个具有两个参数,参数的值都是从可迭代对象中取出,此函数必须遵守的规则为,大于则返回1,小于则返回-1,等于则返回0。
key – 主要是用来进行比较的元素,只有一个参数,具体的函数的参数就是取自于可迭代对象中,指定可迭代对象中的一个元素来进行排序。
reverse – 排序规则,reverse = True 降序 , reverse = False 升序(默认)。
#operator.itemgetter函数
#operator模块提供的itemgetter函数用于获取对象的哪些维的数据,参数为一些序号。
a = [('john', 'A', 15), ('jane', 'B', 12), ('dave', 'B', 10)]
b=operator.itemgetter(1)
b(a)
('jane', 'B', 12)
3.KNN实现鸢尾花分类
import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets
import random
from sklearn.metrics import classification_report
from sklearn.model_selection import train_test_split
import operator
#knn
def knn(x_test,x_train,y_train,k):
#计算x_test 到x_train各点的欧式距离
distance=(((np.tile(x_test,(x_train.shape[0],1))-x_train)**2).sum(axis=1))**0.5
sortdistance=distance.argsort()
classCount={}
for i in range(k):
label=y_train[sortdistance[i]]
classCount[label]=classCount.get(label,0)+1
#统计各标签的数量
sortClassCount=sorted(classCount.items(),key=operator.itemgetter(1),reverse=True)
#对标签字典按键的值进行排序
#获取数量最多的标签
return sortClassCount[0][0]
iris=datasets.load_iris()
x_train,x_test,y_train,y_test=train_test_split(iris.data,iris.target,test_size=0.2)
#分割数据集
print(x_test.shape,x_train.shape)
predictions=[]
for i in range(x_test.shape[0]):#对每个x_test应用knn
predictions.append(knn(x_test[i],x_train,y_train,6))
print(classification_report(y_test,predictions))
(30, 4) (120, 4)
precision recall f1-score support
0 1.00 1.00 1.00 11
1 1.00 0.92 0.96 12
2 0.88 1.00 0.93 7
accuracy 0.97 30
macro avg 0.96 0.97 0.96 30
weighted avg 0.97 0.97 0.97 30
#用sklearn实现
from sklearn.neighbors import KNeighborsClassifier
model=KNeighborsClassifier(n_neighbors=6)
model.fit(x_train,y_train)
prediction1=model.predict(x_test)
print(classification_report(y_test,prediction1))
precision recall f1-score support
0 1.00 1.00 1.00 11
1 1.00 0.92 0.96 12
2 0.88 1.00 0.93 7
accuracy 0.97 30
macro avg 0.96 0.97 0.96 30
weighted avg 0.97 0.97 0.97 30