神经网络的正向传播的理解

前言：

我们先给假设两个条件：

该神经网络全部参数以及拟合到最优

读者以及理解之前的激活函数，矩阵等知识

对于普通函数：

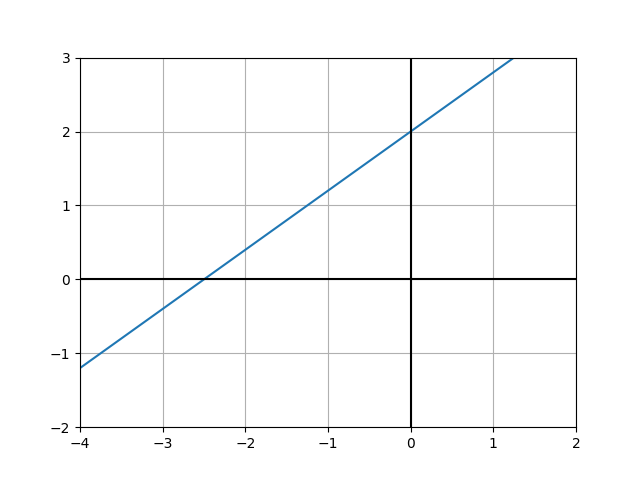
我们先给出一个函数:

将 = 0.8, b = 2, 得到下列图像

若有需求， 给定x， 求出 f ( y ) 的值，我们就可以用代码封装上述函数来实现该需求

如果需求是给定x，大于或等于 f ( y ) 的的时候为1，要如何实现？

在 f ( y ) 后面加一个判断条件即可：

这便是单层感知机

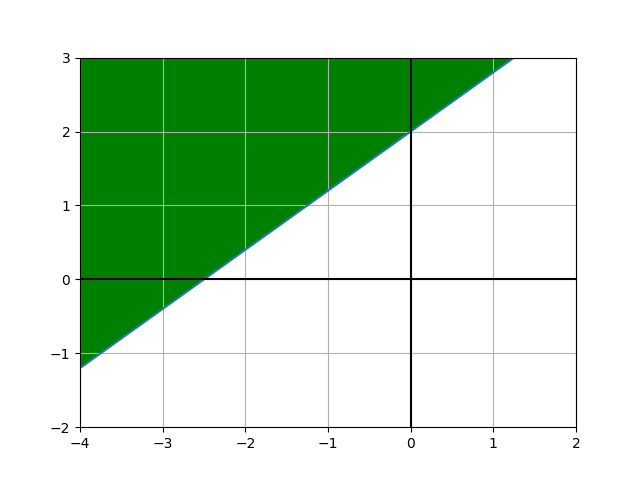
将 = 0.8, b = 2, 得到下列图像

现在把输入改为矩阵输入：

对于单层神经网络：

输出需求改变，输出有两类， 我们的目的就是对不同输入进行分类，使用softmax进行输出分类

设：

这样输出的A与Y将会是：

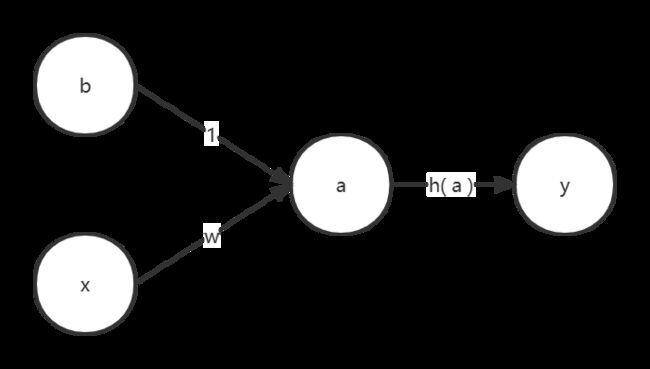
传播图如下：

然后我们尝试理解它，假设所有参数都已经拟合到最优

第一步：

第二步：

y1, y2即为输入对两个分类的概率，最后选取概率最大的一类作为输入被分的类

我们可以用矩阵乘法来代替上述式子：

输出同理，这里对矩阵相乘不过多阐述

【对于输出的准确性，由于权重与偏执都已经被拟合至最优，所以这里不考虑原因】

对于多层神经网络：

上述的即为一个单层神经网络

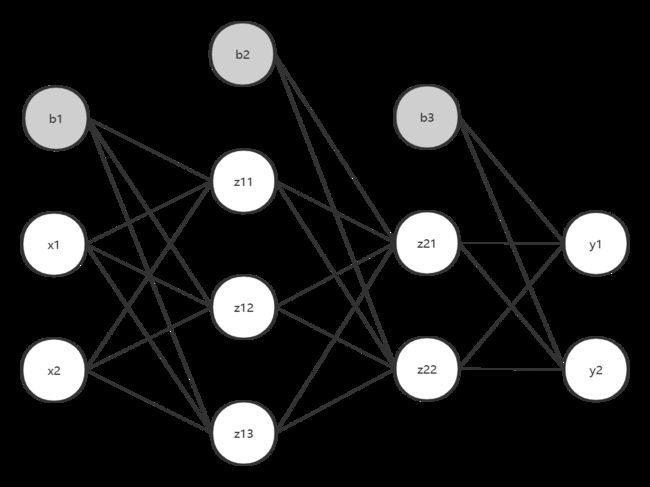
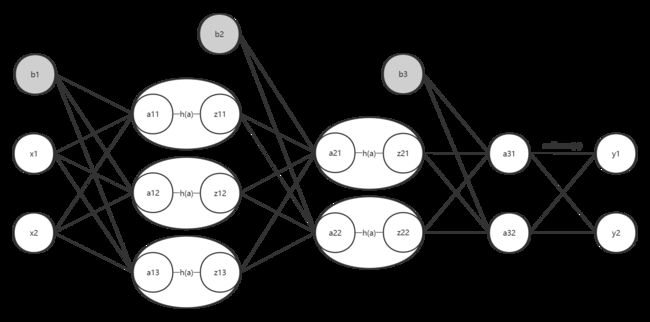
现在我们来看看一个三层神经网络

输入两个维度，输出两个维度。

我们将他的激活函数也画出来

最后softmax()类似全连接层，但性质还是激活函数

我们先设置参数，假装已经参数学习好了

import numpy as np

def init_network():
    network = {}
    network['W1'] = np.array([[0.1, 0.3, 0.5], [0.2, 0.4, 0.6]])  # 2 * 3
    network['b1'] = np.array([0.1, 0.2, 0.3])                     # 1 * 3
    network['W2'] = np.array([[0.1, 0.4], [0.2, 0.5], [0.3, 0.6]])# 3 * 2
    network['b2'] = np.array([0.1, 0.2])                          # 1 * 2
    network['W3'] = np.array([[0.1, 0.3], [0.2, 0.4]])            # 2 * 2
    network['b3'] = np.array([0.1, 0.2])                          # 1 * 2
    
    return network

正向传播：

我们先对第一层进行分析，X为输入，W1， B1为拟合到最优的参数

输入是1*2的矩阵，第一场权重为2*3的矩阵，两者恰好可以相乘，得到1*3的一个矩阵，第一层偏执也为1*3的一个矩阵，即可相加，最后输出一个1*3的矩阵。由于激活函数是单个神经元输入，输出单个神经元，并不改变形状【实际上，激活函数并不一定是单个神经元输入，像softmax，但并不会改变传输矩阵的形状，而且在全连接层中，不是最后一层接输出层的情况下，都采用当个神经元输入的激活函数】

经过第一层计算，我们得到Z1，然后对第二层进行分析：

本层推导与第一层逻辑一样，最后输出一个1*2的矩阵Z2

最后第三层，输出一个1*2的矩阵，经过softmax激活函数，转化为概率，从而进行分类的断与的分类

对于输出层，一帮用() 表示激活函数

过程用代码实现，顺便写上sigmoid, softmax激活函数

def sigmoid(x):
    return 1 / (1 + np.exp(-x)) 

def softmax(a):
    c = np.max(a)
    # 溢出对策
    exp_a = np.exp(a - c)
    sum_exp_a = np.sum(exp_a)
    y = exp_a / sum_exp_a
    
    return y

def forward(network, x):
    W1, W2, W3 = network['W1'], network['W2'], network['W3']
    b1, b2, b3 = network['b1'], network['b2'], network['b3']
    
    a1 = np.dot(x, W1) + b1
    z1 = sigmoid(a1)
    
    a2 = np.dot(z1, W2) + b2
    z2 = sigmoid(a2)
    
    a3 = np.dot(z2, W3) + b3
    y = softmax(a3)
    
    return y

network = init_network()
x = np.array([1.0, 0.5])
y = forward(network, x)

至此，神经网络的正向传播的过程已经说完了，主要注重于过程计算概念的理解

---

对于数字识别神经网络：

我们来看一个数字识别的例子

首先介绍下Mnist数据集：

MNIST数据集(Mixed National Institute of Standards and Technology database)是美国国家标准与技术研究院收集整理的大型手写数字数据库,包含60,000个示例的训练集以及10,000个示例的测试集

然后准备导入数据集：

# 显示图片
# 用PLT比较轻量级，用opencv是比较重量级
from PIL import Image
# 持续化模块：就是让数据持久化保存
import pickle
import numpy as np

# 图片可视化
def img_show(img):
    # print(img)
    # 实现array到image的转换
    pil_img = Image.fromarray(np.uint8(img))
    # print(pil_img)
    pil_img.show()
    
    
# 读取数据集
def _change_one_hot_label(X):
    T = np.zeros((X.size, 10))        # 5 [0, 0, 0 ,0, 0, 1, 0, 0, 0, 0]
    # enumerate() 枚举、列举的意思, 迭代器
    for idx, row in enumerate(T):
        row[X[idx]] = 1
        
    return T


def load_mnist(normalize=True, flatten=True, one_hot_label=False):
    """读入MNIST数据集
    
    Parameters
    ----------
    normalize : 将图像的像素值正规化为0.0~1.0
    one_hot_label : 
        one_hot_label为True的情况下，标签作为one-hot数组返回
        one-hot数组是指[0,0,1,0,0,0,0,0,0,0]这样的数组
    flatten : 是否将图像展开为一维数组
    
    Returns
    -------
    (训练图像, 训练标签), (测试图像, 测试标签)
    """
     
    with open(".\mnist.pkl", 'rb') as f:
        dataset = pickle.load(f)
        
    # 28 * 28 0-255
    
    # 正规化
    if normalize:
        for key in ('train_img', 'test_img'):
            dataset[key] = dataset[key].astype(np.float32)
            dataset[key] /= 255.0
            
    # one-hot 编码 [0, 0, 0 ,0, 0, 1, 0, 0, 0, 0]
    if one_hot_label:
        dataset['train_label'] = _change_one_hot_label(dataset['train_label'])
        dataset['test_label'] = _change_one_hot_label(dataset['test_label'])
    
    # 图像展开为一维 28 * 28 -> 1 * 784
    if not flatten:
         for key in ('train_img', 'test_img'):
            dataset[key] = dataset[key].reshape(-1, 1, 28, 28)

    return (dataset['train_img'], dataset['train_label']), (dataset['test_img'], dataset['test_label']) 

然后我们构建一个3层的神经网络：

各层维度：

输入层维度=784，

第一个隐藏层维度 = 50，

第二个隐藏层维度 = 50，

输出层维度 = 10。

激活函数采用sigmoid，输出激活函数用softmax

构建神经网络

def predict(network, x):
    W1, W2, W3 = network['W1'], network['W2'], network['W3']
    b1, b2, b3 = network['b1'], network['b2'], network['b3']
    
    a1 = np.dot(x, W1) + b1
    z1 = sigmoid(a1)
    
    a2 = np.dot(z1, W2) + b2
    z2 = sigmoid(a2)
    
    a3 = np.dot(z2, W3) + b3
    y = softmax(a3)
    
    return y

现在假设我们已经将模型的参数学习好了

导入已经学习到的参数【pickle.load() 只有Py3.8及以上才可以使用】

def init_network():
    with open(".\model1.pkl", 'rb') as f:
        network = pickle.load(f)
    
    return network

再封装一个读取数据的函数【由于我们是正向传播，就是推导，直接使用验证集】

def get_data():
    (x_train, t_train), (x_test, t_test) = load_mnist(flatten=True, normalize=False, one_hot_label=False)
    return x_test, t_test

然后就可以进行正向传播了

# 获取数据，和标签
x, t = get_data()
# 初始化神经网络的参数
network = init_network()

accuracy_cnt = 0
# 遍历每个数据与标签
for i in range(len(x)):
    # 通过神经网络得到正向传播得到的值
    y = predict(network, x[i])
    p = np.argmax(y)    # 获取概率最高的元素索引
    # 判断是否和标签一值
    if p == t[i]:
        # 记录推导正确的数量
        accuracy_cnt += 1

# 打印正确率
print("Accuracy:", float(accuracy_cnt / len(x)))

---

对于批处理的数字识别神经网络

接下来，尝试结合批处理的正向传播

先初略讲下过程，大体和普通正向传播一样。

设输入 :

该X为 ：

以三为一个批次的输入

再假设：

然后对第一层进行计算，X为3*2的矩阵，W为2*3的矩阵，B为1*3的一个矩阵，输出A应为3*3的一个矩阵，从而可以计算出A:

如果后面接的是softmax激活函数【不考虑中间的激活函数，由于传递方式为神经元对神经元，不会出现顺序打乱或者交叉的情况】，则对每行进行各自的softmax，互不影响，输出Y:

批处理【batch_size = 3】对应的标签形式为：

与神经网络推导出的结果每一列相对应

如果假设X1,X2,X3并不是以批处理的方式输入

对于三个输入，A1,A2,A3:

然后看看接了softmax的情况,与其输入对应的标签形式

我们可以根据普通的神经网络的正向传播来理解批处理情况下神经网络的正向传播，可以发现，传输的数据除了容量不一样之外，并没有其他影响，实际上，由于numpy是有c++编写的，使用批处理可以节省资源开支。

接下来实现批处理的正向传播

# 批处理
x, t = get_data()
network = init_network()

# 一批次大小
batch_size = 100
accuracy_cnt = 0

# 将数据分为批，一批批的进行遍历
for i in range(0, len(x), batch_size):
    # 一次输入网络的批样本
    x_batch = x[i: i+batch_size]
    # 一次输入网络样本的标签
    y_batch = predict(network, x_batch)
    # 计算过真确推导个数
    p = np.argmax(y_batch, axis=1)
    accuracy_cnt += np.sum(p == t[i: i+batch_size])

print("Accuracy:", float(accuracy_cnt / len(x)))

本例用到的model1.pkl与mnistpkl在代码文件同级目录下，如有需要自提。

链接：https://pan.baidu.com/s/1v1ynp1AW7_exWtC8g84Kcw?pwd=0228

提取码：0228