第三周【任务1】学习损失函数(svm多分类损失函数与softmax)
7 损失函数
一、学习内容
-
第三讲损失函数部分,主要介绍了 svm多分类损失函数与softmax函数,以例子详细说明如何使用他们来做完成图像分类任务。指出了svm多分类损失函数存在多解的问题,讲解了使用正则项来解决多解问题。
-
学习的时候需要重点学习svm多分类损失函数与softmax的数学表达式,softmax的作用以及它的最大似然函数,思考Hinge loss与 Softmax的区别
1.SVM
1.1 思考的问题
Q1: 计算car对应的损失时,稍微改变car的分数会有什么结果?

Q2:损失函数的最小值、最大值分别为多少?
如果所有类别都计算正确,那么损失为0,最大值可以为无穷大。
Q3:权重随机初始化,得到的分数均接近于0,此时loss值是多少?
loss等于分类数n-1
![]()
Q4:如果计算所有样本间的分数差包括样本本身的分数,那么损失函数会怎么变化?

Q5:如果使用mean而不是sum会有什么影响?
基本没有影响,仅仅只是缩放了loss的值。
Q6:如果我们把样本分数差做了平方会怎么样?
这就是计算另一种损失函数了
1.2 存在的问题
x = np.array([1,0,1,1])
w1 = np.array([[2,1,1,1],[1,1,0,0]])
w2 = np.array([[4,2,0,2],[1,1,0,0]])
s1 = np.matmul(w1, x) #array([4, 1])
s2 = np.matmul(w2, x) #array([6, 1])
假设分类正确值为第一类,s1和s2的第一个值分数都远大于第二个(4>1,6>1),因此两个的loss都为0,但是两个w不相等
该如何解决这个问题呢?
- 解决方法:可以添加正则项
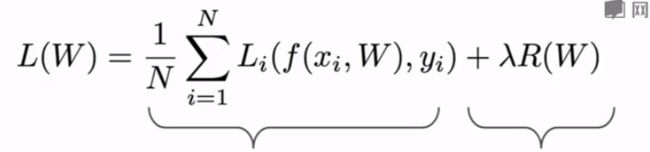
给w1和w2分别计算L2正则化:
w1的二范数为: 2 2 + 1 2 + 1 2 + 1 2 + 1 2 + 1 2 2 = 3 \sqrt[2]{{{2^2}{\rm{ + }}{{\rm{1}}^2}{\rm{ + }}{{\rm{1}}^2}{\rm{ + }}{{\rm{1}}^2}{\rm{ + }}{{\rm{1}}^2}{\rm{ + }}{{\rm{1}}^2}}}{\rm{ = }}3 222+12+12+12+12+12=3
w2的范数为: 4 2 + 2 2 + 0 2 + 2 2 + 1 2 + 1 2 2 = 5.09 \sqrt[2]{{{4^2}{\rm{ + }}{{\rm{2}}^2}{\rm{ + }}{{\rm{0}}^2}{\rm{ + }}{{\rm{2}}^2}{\rm{ + }}{{\rm{1}}^2}{\rm{ + }}{{\rm{1}}^2}}}{\rm{ = }}5.09 242+22+02+22+12+12=5.09
优化的目的是使 L ( w ) L(w) L(w)最小,因此上式两项都要最小,通常正则项是一范数或者二范数,要使 λ R ( w 1 ) \lambda R(w_1) λR(w1)最小,所以选择 w 1 w_1 w1
二分类SVM的推导 是面试中常考的内容
2.Softmax
使用交叉熵计算loss,进行优化
使用交叉熵损失时,label为one-hot形式

2.1 KL散度:
KL散度可以衡量两个分布的相似度,假设两个分布为p,q
公式:本例指的是标签和score之间的相似性
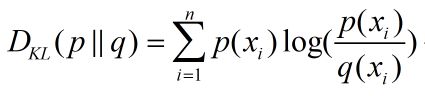
可以变形为:标签的one-hot形式:0–>1000000000
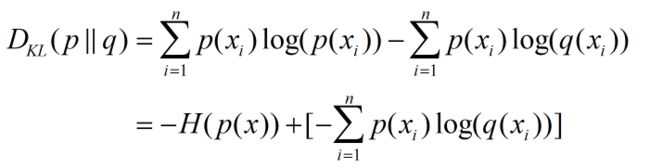
这里的 p ( x i ) p(x_i) p(xi)是one-hot形式, q ( x i ) q(x_i) q(xi)是score
**Eg.**以猫咪 p ( x 0 ) p(x_0) p(x0)为例:
已知 p ( x 0 ) = [ 1 , 0 , 0 ] , p(x_0)=[1,0, 0 ], p(x0)=[1,0,0], q ( x 0 ) = [ 0.13 , 0.87 , 0.00 ] q(x_0)=[0.1 3,0.87,0.00] q(x0)=[0.13,0.87,0.00],
那么, H ( p ( x 0 ) ) = 1 ∗ l o g ( 1 ) + 0 ∗ l o g ( 0 ) + 0 ∗ l o g ( 0 ) = 0 H(p(x_0))=1*log(1)+0*log(0)+0*log(0)=0 H(p(x0))=1∗log(1)+0∗log(0)+0∗log(0)=0

起作用的只有本身对应的这一项
因此,简化为如下式子,即交叉熵可以衡量两个分布的相似性。

一般情况下 p ( x i ) = 1 p(x_i)=1 p(xi)=1,进一步简化为

与最大似然函数相似:

打卡内容:
-
Hinge Loss 表达式
-
加正则的目的
防止模型过拟合,简化函数表达式 -
Softmax 与交叉熵损失公式,分析交叉熵损失的最大值与最小值(softmax 求导要会)
-
Hinge loss与Softmax的区别
