2022.1.1 第十二次周报
文章目录
- 前言
- 一、论文阅读《A Multi-Horizon Quantile Recurrent Forecaster》
-
- 摘要
- Introduction
- Method
-
- Network Architecture
- Loss Function
- Training Scheme
- 总结
- 二、GRU模型学习
-
- 1.GRU概念
- 2.内部结构
-
- 重置门
- tanh
- 更新门
- 输出
- 3.GRU与LSTM的对比
- 4.代码实现
- 总结
前言
This week ,《A Multi-Horizon Quantile Recurrent Forecaster》 has read and analyzed .the paper propose a framework for general probabilistic multi-step time series regression. Paper exploit the expressiveness and temporal nature of Sequence-to-Sequence Neural Networks , the nonparametric nature of Quantile Regression and the efficiency of Direct Multi-Horizon Forecasting. A new training scheme, forking-sequences, is designed for sequential nets to boost stability and performance.In the study of recurrent neural network, I continued to learn the GRU principle and built a simple GRU network model with codes.
本周,我学习了论文《一个多视界分位数递归预测器》,文中提出了一个一般概率多步时间序列回归的框架。论文利用了序列间神经网络的表现力和时间性、分位数回归的非参数性质和直接多视界预测的效率。一种新的训练方案,分叉序列。在递归神经网络的研究中,我继续学习GRU原理,并用代码构建了一个简单的GRU网络模型。
一、论文阅读《A Multi-Horizon Quantile Recurrent Forecaster》
摘要
论文提出了一个用于一般概率多步时间序列回归的框架。具体来说,是利用序列到序列神经网络(例如循环和卷积结构)的表现力和时间特性、分位数回归的非参数特性和直接多水平预测的效率。一种新的训练方案 fork-sequences (分叉序列)专为顺序网络设计,以提高稳定性和性能。实验表明,该方法同时适用于时间和静态协变量,跨多个相关序列学习,季节性变化,未来计划的事件峰值和现实生活中的大规模预测中的冷启动问题。本文通过预测亚马逊上所售商品的未来需求以及在电价和负荷的预测竞赛中展示该框架的性能。
Introduction
时间序列预测问题有两种预测的策略:
递归预测:即每次预测一个值,然后作为真实标签输入模型,继续预测,直到达到预测长度,称为Recursive strategy。该策略需要精心设计,否则会造成误差的累积。
直接预测:即一次直接预测指定长度的值,称为Multi-Horizon strategy。该策略避免了误差累积,但通过共享参数保持了效率。
许多决策场景需要概率预测模型提供更丰富的信息,该模型返回完整的条件分布p(yt+k|y:t),而不是仅预测条件均值E(yt+k|y:t)的点预测模型。一个典型的例子是由于预测过度和预测不足而导致成本不对称的任务。那么,条件均值最小化的对称均方误差(symmetric Mean Squared Error)并不能反映真实的损失。对于实值时间序列,概率预测传统上是通过假设残差序列 yt−yt 上的误差分布或随机过程(通常为高斯)来实现的。然而,精确的参数分布在应用中往往没有直接关系。
为了协调和改进这些单独的方法,论文提出MQ-R©NN:一个生成多水平分位数预测的Seq2Seq框架。该模型旨在解决大规模时间序列回归问题:

其中 y·,i 是要预测的第 i 个时间序列,x(h) :t,i 是历史中可用的时间协变量,x(f) t:,i 是关于未来的知识,x(s) i是静态的、时不变的特征。每个序列都被视为一个样本输入单个 RNN 或 CNN,即使它们对应于不同的条目。这可以对历史有限的条目进行跨序列学习和冷启动预测。
论文详细演示了每种方法的单个属性如何在框架中无缝结合,并在多个预测应用程序中实现比最先进模型更好的性能。本文的主要贡献还包括:
提出了一种序列神经网络与多水平预测相结合的有效训练方案。这种方法,我们称之为分叉序列,并在3.3节中详细介绍,可以通过在数据序列上的所有时间点上进行训练,极大地提高编码器-解码器式循环网络或ConvNets的训练稳定性和性能,在这些时间点上将创建预测。
•我们设计了一个网络子结构,以适应以前很少关注的问题:如何解释已知的未来信息,包括季节性变化和导致大幅峰值和下降的已知事件的对齐。
Method
Network Architecture
论文提出的模型类似于 RNN Seq2Seq 模型(Fig.1(a))使用 vanilla LSTM 将所有历史编码为隐藏状态 ht。但是 MQ-RNN 没有使用 LSTM 作为递归解码器,而是设计了两个 MLP 分支(Fig.1(b))。第一个(全局)MLP 将编码器输出和所有未来输入汇总到两个上下文中:针对 K 个未来点中的每一个一系列特定时段(horizon-specific)上下文 ct+k,以及捕获公共信息的与时段无关(horizon-agnostic)的上下文 ca:
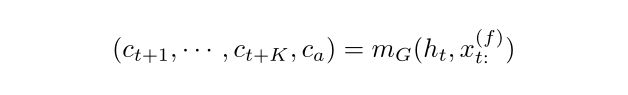
其中 mG(·) 是全局 MLP,上下文 c(·) 每个都可以具有任意维度。第二个(局部)MLP 适用于每个特定的时段。它结合了相应的未来输入和前面描述的全局 MLP 的两个上下文,然后输出该特定未来时间步长所需的所有分位数:
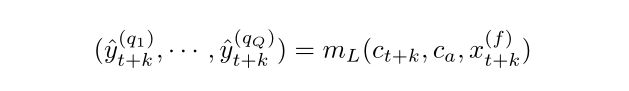
其中 mL(·) 是局部 MLP,其参数在所有层 k ∈ {1,····K} 中共享,q(·) 表示 Q 分位数中的每一个。整体结构下图。
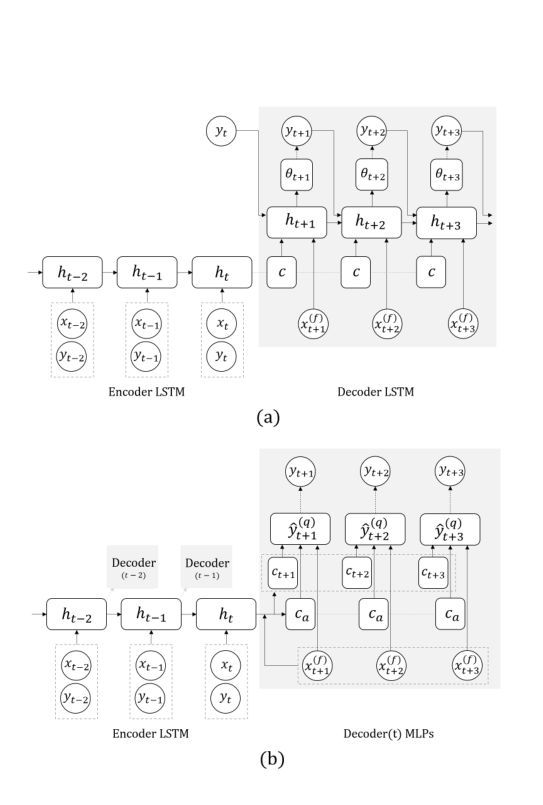
图 1. 用于多步预测的神经网络架构。圆圈和正方形分别表示观察节点和隐藏节点。虚线框将节点展平为向量。虚线表示复制。虚线箭头是损失,它将网络输出和目标联系起来。 xt = (x(h) t , x(f) t , x(s))。未显示层深度。 (a) Seq2SeqC,其中损失函数是似然函数(例如,用于文本生成的多项式,用于数值的高斯函数),由 θt 参数化。在预测时,^yt+k 被输入解码器,而不是训练中的 yt+k。 (b) MQ-RNN,其中总损失函数是单个分位数损失的总和,输出是对不同 q 值的所有分位数预测。在训练过程中,时间序列被分叉:每个循环层对应一个解码器,具有相同的权重(阴影框)。
Loss Function
在分位数回归中,训练模型以最小化总分位数损失 (Quantile Loss,QL):

其中 (·)+ = max(0,·)。当 q = 0.5 时,QL 就是平均绝对误差(Mean Absolute Error,MAE),它的最小值是预测分布的中位数。设 K 是预测的层数,Q 是感兴趣的分位数,那么 K × Q 矩阵 Y ~ = [y~(q) t+k]k,q 是参数模型 g(y: t, x, θ) 的输出。
Training Scheme
我们的模型相对于Seq2Seq的一个主要性能增益是通过下面描述的分叉序列训练方案实现的。请注意,所有Seq2Seq风格的模型都在输入序列中有一个结束点,例如自然语言中的一个停止符号,这个结束点是编码器和解码器交换信息的地方。在预测中,这个停止符号自然是预测创建时间(FCT),即必须在此时间步长生成对未来范围的预测。
与许多其他顺序建模问题不同,时间序列预测通常需要在每个可能的时间点生成,即每天或每周都需要进行预测。大多数应用程序使用切割序列:在一组随机选择的FCT上分割时间序列,并使用每个序列/FCT对作为训练示例。这在预测中也被称为移动窗口方案,需要大量的数据增强。
在前面的部分中,描述了 MQ-RNN 的核心设计:一系列预测分位数的多层次、面向未来的分叉解码器。在这里,我们讨论了编码器的一些实际扩展,以超越普通 LSTM 并进一步提高性能。
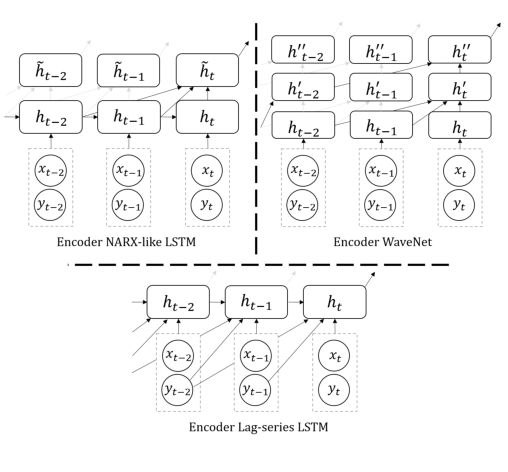
MQ-RNN 的替代编码器(与图 1b 进行比较和对比)。为清楚起见,未显示所有分叉解码器,对最后一个解码器没有贡献的连接以灰色显示。请注意,LSTM 编码器中的 ht 来自 LSTM 单元,而在 WaveNet 中,所有隐藏状态都来自扩散的果卷积(dilated causal convolutions)。
LSTM 被提出来避免梯度消失并扩展 RNN 的长期记忆容量。许多预测问题具有较长的周期性(例如 365 天),并且可能会在循环前向传播期间遭受记忆损失。另一种不那么知名的用于解决相同长依赖问题的循环网络类型是 NARX RNN (DiPietro et al, 2017),它不仅基于 ht-1 计算隐藏状态 ht,还基于一组特定的其他过去状态,例如(ht−2,····,ht−D)。这也称为跳过连接。过去状态的存在降低了对 RNN 单元记忆长依赖的能力的要求。在 MQ-RNN 中启用 NARX-ish 编码器的一个简单修改是在 LSTM 之上放置一个额外的线性层来总结过去的状态:〜ht = m(ht, · · · , ht−D),然后将〜ht 输入到全局 MLP 解码器。请注意,通过在每个循环层及最后一层的状态上放置相同的 m(·),此操作与分叉序列优化兼容。
NARX-ish 编码器在实验中确实比普通 LSTM 带来了改进。但是一个看似简单的替代方案表现得更好:只需将过去的序列 (yt−1, · · · , yt−D) 作为滞后特征输入与 yt 一起输入到 t 处的循环层。事实上,这在将输入序列的过去值通过循环层之前有效地构造了跳过连接,而不是在 RNN 之后进行跳过连接。这个简单的滞后序列技巧之所以奏效,可能是由于预测的性质:时间序列的历史值是我们对它的未来值拥有的最具预测性的信息,因此对隐藏状态的影响最大。因此,滞后系列可以更好地逼近真实的 NARX 编码器,其中 ht 被遥远的过去更新。
总结
在第4节中,我们在亚马逊零售需求时间序列的大型数据集上演示了MQ-R©NN的价值,以及来自公共电力预测比赛的数据。第5节总结了一些结论,并概述了未来研究的可能方向,这里就不介绍了。总体而言,论文提出了一个概率时间序列回归的通用框架,并展示了每个新组件如何对最先进的最终性能做出贡献。我们的发现可以帮助设计实用的大规模预测应用程序和编码器解码器风格的深度学习架构。
二、GRU模型学习
1.GRU概念
GRU(Gate Recurrent Unit)是循环神经网络(Recurrent Neural Network, RNN)的一种。和LSTM(Long-Short Term Memory)一样,也是为了解决长期记忆和反向传播中的梯度等问题而提出来的。相比LSTM,使用GRU能够达到相当的效果,并且相比之下更容易进行训练,能够很大程度上提高训练效率,因此很多时候会更倾向于使用GRU。

有一个当前的输入Xt,和上一个节点传递下来的隐状态(hidden state)ht-1 ,这个隐状态包含了之前节点的相关信息。
结合Xt和 ht-1 ,GRU会得到当前隐藏节点的输出yt和传递给下一个节点的隐状态 ht。
2.内部结构
一个单元的结构
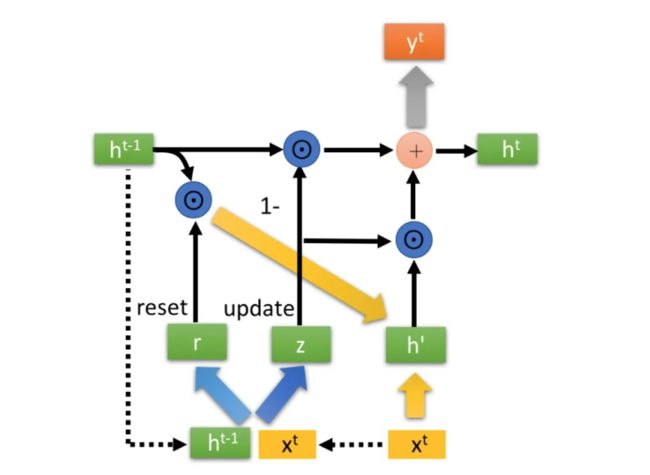
其中包括reset(重置门rt)和update(更新门zt),以及tanh和Hadamard Product等计算公式。
重置门
这里使用的是sigmoid函数,通过这个函数可以将数据变换为0-1范围内的数值,从而来充当门控信号。(下面更新门也是一样)
这里重置门的意义:根据当前的输入Xt和上一个节点传递下来的隐状态(hidden state)ht-1 进行匹配,将两者之间的相关程度做一个计算,例如对当前的输入Xt进行分析的时候,需要根据上一个节点传递下来的隐状态(hidden state)ht-1做推断,最后求出一组总和为1的概率。
tanh

这里需要用到 当前的输入Xt和上一个节点传递下来的隐状态(hidden state)ht-1 以及重置门rt 求出的概率。
先将当前的输入Xt和重置门rt 求出的概率进行相乘,再结合上一个节点传递下来的隐状态(hidden state)ht-1求出相关性最紧密的内容,再通过一个tanh激活函数来将数据放缩到-1~1的范围内。
更新门
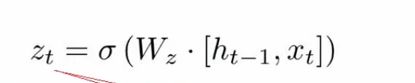
更新门也是使用了sigmoid函数,这个门的意义是把上面求到的h~进行再次计算相关性,得出有用于当前单元的数据。
输出
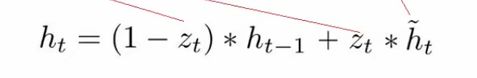
这一步的操作就是忘记传递下来的ht-1中的某些维度信息,并加入当前节点输入的某些维度信息。
简而言之:1、把上一个节点传递下来的隐状态(hidden state)ht-1相关性很弱的数据清除掉,保留有用的数据
2、根据上一个节点传递下来的隐状态(hidden state)ht-1,计算当前的的输入Xt,把重复的、没用的数据删除掉,保留有用的。
计算流程:
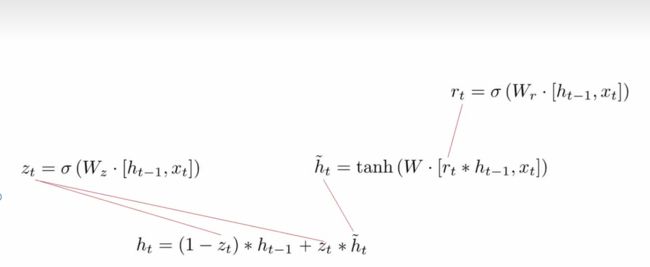
GRU很聪明的一点就在于,我们使用了同一个门控Z就同时可以进行遗忘和选择记忆(LSTM则要使用多个门控),可以看到,这里的遗忘Z和选择(1-Z)是联动的。也就是说,对于传递进来的维度信息,我们会进行选择性遗忘,则遗忘了多少权重 (Z),我们就会使用包含当前输入的h~中所对应的权重进行弥补(1-Z)。以保持一种”恒定“状态。
3.GRU与LSTM的对比
GRU是在2014年提出来的,而LSTM是1997年。他们的提出都是为了解决相似的问题。
RNN:有两个输入,两个输出。
LSTM:有三个输入,三个输出。
GRU:有两个输入,两个输出。
与LSTM相比,GRU内部少了一个”门控“,参数比LSTM少,但是却也能够达到与LSTM相当的功能。考虑到硬件的计算能力和时间成本,因而很多时候我们也就会选择更加”实用“的GRU啦。
4.代码实现
import torch
import d2l.torch
from torch import nn
batch_size, num_steps = 32, 35
train_iter, vocab = d2l.torch.load_data_time_machine(batch_size, num_steps)
def get_params(vocab_size, num_hiddens, device):
input_size = output_size = vocab_size
def normal(shape):
return torch.randn(size=shape, device=device) * 0.01
def three():
return (normal(shape=(input_size, num_hiddens)),
normal(shape=(num_hiddens, num_hiddens)),
torch.zeros(num_hiddens, device=device))
W_xr, W_hr, b_r = three() # 更新门参数
W_xz, W_hz, b_z = three() # 重置门参数
W_xh, W_hh, b_h = three() # 候选隐状态参数
# 输出层参数
W_hq = normal(shape=(num_hiddens, output_size))
b_q = torch.zeros(output_size, device=device)
# 设置参数梯度为True
params = [W_xr, W_hr, b_r, W_xz, W_hz, b_z, W_xh, W_hh, b_h, W_hq, b_q]
for param in params:
param.requires_grad_(True)
return params
def init_gru_state(batch_size, num_hiddens, device):
return (torch.zeros(size=(batch_size, num_hiddens), device=device),)
def gru(inputs, state, params):
W_xr, W_hr, b_r, W_xz, W_hz, b_z, W_xh, W_hh, b_h, W_hq, b_q = params
H, = state
outputs = []
for X in inputs:
R = torch.sigmoid((X @ W_xr) + (H @ W_hr) + b_r)
Z = torch.sigmoid((X @ W_xz) + (H @ W_hz) + b_z)
H_tilda = torch.tanh((X @ W_xh) + ((R * H) @ W_hh) + b_h)
H = Z * H + (1 - Z) * H_tilda
Y = H @ W_hq + b_q
outputs.append(Y)
return torch.cat(outputs, dim=0), (H,)
vocab_size, num_hiddens, device = len(vocab), 256, d2l.torch.try_gpu()
num_epochs, lr = 500, 1
model = d2l.torch.RNNModelScratch(vocab_size, num_hiddens, device, get_params, init_gru_state, gru)
d2l.torch.train_ch8(model, train_iter, vocab, lr, num_epochs, device, use_random_iter=False)
总结
本周学习了GRU模型,发现GRU模型相比于LSTM模型简单了不少,同时也具备了LSTM的功能,而且参数也更加少,方便模型的训练。同时阅读了《A Multi-Horizon Quantile Recurrent Forecaster》这篇论文,学习了一个概率多步时间序列回归的框架。
