图像分割-区域生长
一、图像分割概述
所谓图像分割是指根据灰度、彩色、空间纹理、几何形状等特征把图像划分成若干个互不相交的区域,使得这些特征在同一区域内表现出一致性或相似性,而在不同区域间表现出明显的不同。简单的说就是在一副图像中,把目标从背景中分离出来。
二、简单分类
传统分割方法
1、基于阈值的图像分割
2、基于区域的图像分割
3、基于边缘检测的图像分割
结合特定工具的图像分割算法
1、基于遗传算法的图像分割
2、基于主动轮廓模型的分割方法
3、基于深度学习的分割
三、基于区域生长的图像分割
基于区域的分割方法是以直接寻找区域为基础的分割技术,基于区域提取方法有两种基本形式:一种是区域生长,从单个像素出发,逐步合并以形成所需要的分割区域;另一种是从全局出发,逐步切割至所需的分割区域。
区域生长
区域增长方法是根据同一物体区域内像素的相似性质来聚集像素点的方法,从初始区域(如小邻域或甚至于每个像素)开始,将相邻的具有同样性质的像素或其它区域归并到目前的区域中从而逐步增长区域,直至没有可以归并的点或其它小区域为止。区域内像素的相似性度量可以包括平均灰度值、纹理、颜色等信息。
区域增长方法是一种比较普遍的方法,在没有先验知识可以利用时,可以取得最佳的性能,可以用来分割比较复杂的图象,如自然景物。但是,区域增长方法是一种迭代的方法,空间和时间开销都比较大。
区域生长的好坏决定于:
1.初始点(种子点)的选取。
2.生长准则。
3.终止条件。
区域生长的原理
区域生长的基本思想是将具有相似性质的像素集合起来构成区域。具体先对每个需要分割的区域找一个种子像素作为生长起点,然后将种子像素和周围邻域中与种子像素有相同或相似性质的像素(根据某种事先确定的生长或相似准则来判定)合并到种子像素所在的区域中。将这些新像素当作新的种子继续上面的过程,直到没有满足条件的像素可被包括进来。这样一个区域就生长成了。
下面给出一个区域生长的实例:图(a)为原始图像,数字表示像素的灰度。以灰度值为8的像素为初始的生长点,记为f(i,j)。在8邻域内,生长准则是待测点灰度值与生长点灰度值相差为1或0。那么图(b)是第一次区域生长后,f(i-1,j)、f(i,j-1)、f(i,j+1)和生长点灰度值相差都是1,因而被合并。图(c)是第二次生长后,f(i+1,j)被合并。图(d)为第三次生长后,f(i+1,j-1)、f(i+2,j)被合并,至此,已经不存在满足生长准则的像素点,生长停止。
![]()
四、例子
4.1经典区域生长方法
4.1.1鼠标选取单种子点
预处理操作:
使用中值滤波去噪,中值滤波能达到噪声被消除,而边缘还完好保留的效果。
A=imread('jx_3.jpg');
imshow(A);
title('原图像');
B=rgb2gray(A);
C=medfilt2(B,[3,3]); %利用中值滤波消除噪声
figure,imshow(C);
title('去噪后图像');鼠标选取单种子点
I=double(C); %转换为灰度值是0-1的双精度
[M,N]=size(I);
J=zeros(M,N); %定义输出图像矩阵,初始为零矩阵
msgbox('请用鼠标单击选择一种子点并按回车键', '操作','modal');
[y,x]=getpts; %通过鼠标获得区域生长起始点
xr=round(x);
yr=round(y);
seed=I(xr,yr);
J(xr,yr)=1; %将J中与所取点相对应位置的点设置为白点
graysum=seed; %储存符合区域生长条件的点的灰度值的总和
pointsum=1; %储存符合区域生长条件的点的总个数
count=1; %每次判断一点周围八点符合条件的新点的数目
threshold=20; %阈值
while count>0 %判断是否有新的符合生长条件的点,若没有,则结束
s=0; %记录判断一点周围八点时,符合条件的新点的灰度值之和
count=0;
for i=1:M
for j=1:N
if J(i,j)==1
if (i-1)>0 && (i+1)<(M+1) && (j-1)>0 && (j+1)<(N+1) %判断此点是否为图像边界上的点
for u= -1:1 %判断点周围八点是否符合阈值条件
for v= -1:1 %u,v为偏移量
if J(i+u,j+v)==0 && abs(I(i+u,j+v)-seed)<=threshold %判断是否未存在于输出矩阵J,并且为符合阈值条件的点
J(i+u,j+v)=1; %将符合以上两条件的点在J中与之位置对应的点设置为白点
count=count+1;
s=s+I(i+u,j+v);
end
end
end
end
end
end
end
pointsum=pointsum+count;
graysum=graysum+s;
seed=graysum/pointsum; %计算新的灰度平均值
end
figure,imshow(J);
title('分割后图像');结果与种子点的选取位置有关,同时不连通的区域无法被一起分割出来
鼠标选取多个种子数
A=imread('colon.bmp');
imshow(A);
title('原图像');
B=rgb2gray(A);
C=medfilt2(B,[3,3]); %利用中值滤波消除噪声
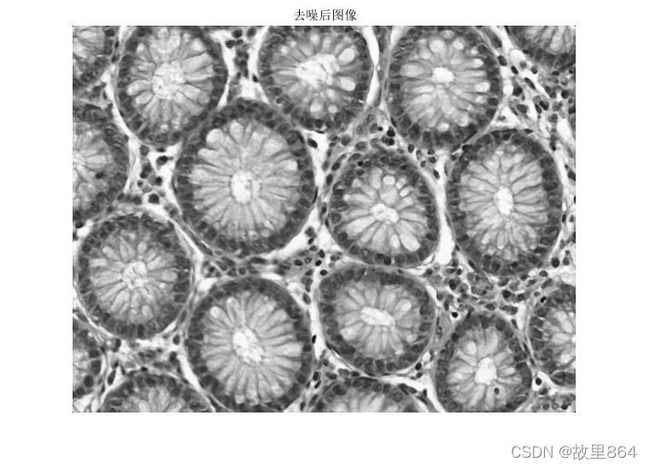
figure,imshow(C);
title('去噪后图像');
%鼠标选取多个种子数
I=double(C); %转换为灰度值是0-1的双精度
[M,N]=size(I);
J=zeros(M,N); %定义输出图像矩阵,初始为零矩阵
msgbox('请用鼠标单击选择多个种子点并按回车键', '操作','modal');
[y,x]=getpts; %通过鼠标获得区域生长起始点(getpts函数本身就可以获得多个点,并返回多个点的坐标)
xr=round(x);
yr=round(y);
threshold=10; %阈值
T=length(xr);
for k=1:T %循环,依次以当选取的各点为种子点进行区域分割
seed=I(xr(k),yr(k));
J(xr(k),yr(k))=1; %将J中与所取点相对应位置的点设置为白点
graysum=seed; %储存符合区域生长条件的点的灰度值的总和
pointsum=1; %储存符合区域生长条件的点的总个数
count=1; %每次判断一点周围八点符合条件的新点的数目
while count>0 %判断是否有新的符合生长条件的点,若没有,则结束
s=0; %记录判断一点周围八点时,符合条件的新点的灰度值之和
count=0;
for i=1:M
for j=1:N
if J(i,j)==1
if (i-1)>0 && (i+1)<(M+1) && (j-1)>0 && (j+1)<(N+1) %判断此点是否为图像边界上的点
for u= -1:1 %判断点周围八点是否符合阈值条件
for v= -1:1 %u,v为偏移量
if J(i+u,j+v)==0 && abs(I(i+u,j+v)-seed)<=threshold %判断是否未存在于输出矩阵J,并且为符合阈值条件的点
J(i+u,j+v)=1; %将符合以上两条件的点在J中与之位置对应的点设置为白点
count=count+1;
s=s+I(i+u,j+v);
end
end
end
end
end
end
end
pointsum=pointsum+count;
graysum=graysum+s;
seed=graysum/pointsum; %计算新的灰度平均值
end
end
figure,imshow(J);
title('分割后图像');4.2分水岭方法
传统分水岭算法(watershed)的基本思想是将图像看做为地理学的拓扑地貌,将图像想象成一个立体的地形表面。图像中的每一个像素的灰度值作为该点的海拔高度,每一个局部极小值及它影响的区域被称为集水盆,则集水盆的边界就形成了分水岭。分水岭的概念和形成能够通过模拟浸入的过程来说明,假设在每个区域极小值的位置刺穿一个小孔,从孔中向该区域不断注水,则地势较低的区域会首先被淹没,在浸入加深的过程中,每一个局部极小值的影响域都处在慢慢扩展过程中,当水淹没到一定高度时两个集水盆会相连合并为同一个区域,此时应在两个集水盆汇合处构筑“大坝”来阻止区域合并,最终形成分水岭,这些“大坝”的边界对应于分水岭的分割线,同时也是由分水岭算法提取出的连续边界轮廓。要实现分水岭方法,可分为以下几步进行:读入图像,求取图像的边界,应用分割算法。
I = C;
hy = fspecial('sobel'); %sobel算子
hx = hy';
Iy = imfilter(double(I), hy, 'replicate'); %滤波求y方向边缘
Ix = imfilter(double(I), hx, 'replicate'); %滤波求x方向边缘
gradmag = sqrt(Ix.^2 + Iy.^2); %求摸
figure,imshow(gradmag,[]), %显示梯度
title('Gradient magnitude (gradmag)')
L = watershed(gradmag); %直接应用分水岭算法
Lrgb = label2rgb(L); %转化为彩色图像
figure,imshow(Lrgb), %显示分割后的图像
title('Watershed transform of gradient magnitude (Lrgb)')
可以看出,传统的分水岭方法对该图像分割效果较差,过分割现象明显。传统分水岭算法虽对微弱的边缘具有良好的响应,但对图像中噪声,物体表面细微的灰度变化比较敏感,噪声会恶化图像梯度进而造成分割结果轮廓偏移,通常的分割结果会出现严重的“过分割”现象。因此要想通过分水岭方法得到更好的图像分割效果,必须对其算法进行改进。