分类算法学习(二)逻辑回归
文章目录
- 分类算法之逻辑回归
-
- 逻辑回归
- 属性
- 特点分析
- 案例----乳腺癌分类
-
- 第一步:导入需要的各种包
- 第二步:设置显示中文字体和正常显示符号
- 第三步:拦截异常
- 第四步:读取数据
- 第五步:异常数据处理
- 第六步:数据提取以及数据分割
- 第七步:数据分割
- 第八步:数据归一化
- 第九步:模型训练
- 第十步:模型评估
- 第十一步:数据预测
- 第十二步:画图
分类算法之逻辑回归
逻辑回归(Logistic Regression),简称LR。它的特点是能够是我们的特征输入集合转化为0和1这两类的概率。一般来说,回归不用在分类问题上,因为回归是连续型模型,而且受噪声影响比较大。如果非要应用进入,可以使用逻辑回归。
优点:计算代价不高,易于理解和实现
缺点:容易欠拟合,分类精度不高
适用数据:数值型和标称型
逻辑回归
Logistic回归本质上是线性回归,只是在特征到结果的映射中加入了一层函数映射,即先把特征线性求和,然后使用函数g(z)将最为假设函数来预测。g(z)可以将连续值映射到0和1上。Logistic回归用来分类0/1问题,也就是预测结果属于0或者1的二值分类问题
映射函数为:
g ( z ) = 1 1 + e − z g\left({z}\right){=}\frac{1}{1+e^-z} g(z)=1+e−z1
其中 z = θ 0 + θ 1 x 1 + θ 2 x 2 + . . . z{=}\theta_{0}+\theta_{1}{x_{1}}+\theta_{2}{x_{2}}{+...} z=θ0+θ1x1+θ2x2+...
映射出来的效果如下如:

sklearn.linear_model.LogisticRegression
逻辑回归类
class sklearn.linear_model.LogisticRegression(penalty='l2', dual=False, tol=0.0001, C=1.0, fit_intercept=True, intercept_scaling=1, class_weight=None, random_state=None, solver='liblinear', max_iter=100, multi_class='ovr', verbose=0, warm_start=False, n_jobs=1)
"""
:param C: float,默认值:1.0
:param penalty: 特征选择的方式
:param tol: 公差停止标准
"""
from sklearn.model_selection import train_test_split
from sklearn.datasets import load_digits
from sklearn.linear_model import LogisticRegression
LR = LogisticRegression(C=1.0, penalty='l1', tol=0.01)
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.33, random_state=42)
LR.fit(X_train,y_train)
LR.predict(X_test)
LR.score(X_test,y_test)
0.96464646464646464
# c=100.0
0.96801346801346799
属性
coef_
决策功能的特征系数
Cs_
数组C,即用于交叉验证的正则化参数值的倒数
特点分析
**
决策功能的特征系数
Cs_
数组C,即用于交叉验证的正则化参数值的倒数
案例----乳腺癌分类
第一步:导入需要的各种包
import numpy as np
import pandas as pd
import matplotlib as mpl
import matplotlib.pyplot as plt
import warnings # 警告处理
from sklearn.linear_model import LogisticRegressionCV # 逻辑回归模型
from sklearn.linear_model.coordinate_descent import ConvergenceWarning # 警告处理
from sklearn.model_selection import train_test_split # 数据划分
from sklearn.preprocessing import StandardScaler # 数据标准化
from matplotlib.font_manager import FontProperties
第二步:设置显示中文字体和正常显示符号
# 设置显示中文字体
my_font = FontProperties(fname="/usr/share/fonts/chinese/simsun.ttc")
# fontproperties = my_font
# 设置正常显示符号
mpl.rcParams["axes.unicode_minus"] = False
第三步:拦截异常
warnings.filterwarnings(action = 'ignore', category = ConvergenceWarning)
第四步:读取数据
path = '/root/zhj/python3/code/data/breast-cancer-wisconsin.data'
names = ['id','Clump Thickness','Uniformity of Cell Size','Uniformity of Cell Shape',
'Marginal Adhesion','Single Epithelial Cell Size','Bare Nuclei',
'Bland Chromatin','Normal Nucleoli','Mitoses','Class']
df = pd.read_csv(path, header=None, names=names)
第五步:异常数据处理
datas = df.replace('?', np.nan) # 将非法字符"?"替换为np.nan
datas = datas.dropna(how = 'any') # 将行中有空值的行删除
第六步:数据提取以及数据分割
# 第一列数据为id,对分类决策没有帮助,所以无需作为特征数据
X = datas[names[1:10]]
Y = datas[names[10]]
第七步:数据分割
# test_size:测试集所占比例
# random_state:保证每次分割所产生的数据集是完全相同的
X_train, X_test, Y_train, Y_test = train_test_split(X, Y, test_size=0.2, random_state=0)
第八步:数据归一化
ss = StandardScaler() # 创建归一化
X_train = ss.fit_transform(X_train) # 训练模型及归一化数据
第九步:模型训练
# 构建模型
# Logistic回归是一种分类算法,不能应用于回归中(也即是说对于传入模型的y值来讲,不能是float类型,必须是int类型)
lr = LogisticRegressionCV(multi_class='ovr',fit_intercept=True, Cs=np.logspace(-2, 2, 20),
cv=2, penalty='l2', solver='lbfgs', tol=0.01)
"""
multi_class: 分类方式参数
参数可选: ovr(默认)、multinomial
这两种方式在二元分类问题中,效果是一样的;在多元分类问题中,效果不一样
ovr: one-vs-rest, 对于多元分类的问题,先将其看做二元分类,分类完成后,再迭代对其中一类继续进行二元分类
multinomial: many-vs-many(MVM),即Softmax分类效果
penalty: 过拟合解决参数,l1或者l2
solver: 参数优化方式
当penalty为l1的时候,参数只能是:liblinear(坐标轴下降法);
nlbfgs和cg都是关于目标函数的二阶泰勒展开
当penalty为l2的时候,参数可以是:lbfgs(拟牛顿法)、newton-cg(牛顿法变种),seg(minibatch)
维度<10000时,lbfgs法比较好;维度>10000时,cg法比较好;显卡计算的时候,lbfgs和cg都比seg快
"""
# 模型训练
re=lr.fit(X_train, Y_train)
第十步:模型评估
r = re.score(X_train, Y_train)
print ("R值(准确率):", r)
print ("稀疏化特征比率:%.2f%%" % (np.mean(lr.coef_.ravel() == 0) * 100))
print ("参数:",re.coef_)
print ("截距:",re.intercept_)
print(re.predict_proba(X_test)) # 获取sigmoid函数返回的概率值
R值(准确率): 0.97619047619
稀疏化特征比率:0.00%
参数: [[ 0.9402831 0.36380614 0.55630627 0.5494959 0.49355712 1.1403515
0.82238663 0.68524875 0.34734485]]
截距: [-1.0872036]
[[ 5.18792508e-05 9.99948121e-01]
[ 3.32650120e-04 9.99667350e-01]
[ 2.87547763e-13 1.00000000e+00]
[ 3.99680289e-15 1.00000000e+00]
[ 4.94149421e-03 9.95058506e-01]
[ 3.65707020e-04 9.99634293e-01]
[ 1.41502942e-05 9.99985850e-01]
[ 0.00000000e+00 1.00000000e+00]
[ 2.76984648e-04 9.99723015e-01]
[ 2.17723400e-03 9.97822766e-01]
[ 0.00000000e+00 1.00000000e+00]
[ 2.87741294e-05 9.99971226e-01]
[ 0.00000000e+00 1.00000000e+00]
[ 3.32650120e-04 9.99667350e-01]
[ 4.51860458e-06 9.99995481e-01]
[ 4.01864009e-09 9.99999996e-01]
[ 1.33226763e-15 1.00000000e+00]
[ 0.00000000e+00 1.00000000e+00]
[ 0.00000000e+00 1.00000000e+00]
[ 1.66803025e-05 9.99983320e-01]
[ 3.32650120e-04 9.99667350e-01]
[ 7.50061373e-05 9.99924994e-01]
[ 6.37732089e-11 1.00000000e+00]
[ 7.56765575e-04 9.99243234e-01]
[ 2.22044605e-16 1.00000000e+00]
[ 0.00000000e+00 1.00000000e+00]
[ 5.57889770e-05 9.99944211e-01]
[ 4.83103577e-04 9.99516896e-01]
[ 1.15483642e-04 9.99884516e-01]
[ 4.44089210e-16 1.00000000e+00]
[ 4.94149421e-03 9.95058506e-01]
[ 0.00000000e+00 1.00000000e+00]
[ 0.00000000e+00 1.00000000e+00]
[ 1.46187658e-04 9.99853812e-01]
[ 2.95666394e-04 9.99704334e-01]
[ 1.46187658e-04 9.99853812e-01]
[ 2.22044605e-16 1.00000000e+00]
[ 1.44328993e-14 1.00000000e+00]
[ 2.95666394e-04 9.99704334e-01]
[ 0.00000000e+00 1.00000000e+00]
[ 1.49441421e-05 9.99985056e-01]
[ 1.93367503e-06 9.99998066e-01]
[ 4.98235624e-04 9.99501764e-01]
[ 1.23908422e-03 9.98760916e-01]
[ 4.94149421e-03 9.95058506e-01]
[ 1.47784358e-04 9.99852216e-01]
[ 1.97492852e-03 9.98025071e-01]
[ 0.00000000e+00 1.00000000e+00]
[ 3.84829040e-05 9.99961517e-01]
[ 1.15483642e-04 9.99884516e-01]
[ 1.77635684e-15 1.00000000e+00]
[ 5.17785856e-05 9.99948221e-01]
[ 1.44328993e-14 1.00000000e+00]
[ 4.79841615e-05 9.99952016e-01]
[ 1.66803025e-05 9.99983320e-01]
[ 8.72065499e-06 9.99991279e-01]
[ 0.00000000e+00 1.00000000e+00]
[ 2.33590924e-13 1.00000000e+00]
[ 5.83866529e-07 9.99999416e-01]
[ 4.44089210e-16 1.00000000e+00]
[ 9.57806006e-04 9.99042194e-01]
[ 1.58515721e-03 9.98414843e-01]
[ 3.74258261e-04 9.99625742e-01]
[ 7.56765575e-04 9.99243234e-01]
[ 1.46187658e-04 9.99853812e-01]
[ 9.57806006e-04 9.99042194e-01]
[ 9.57806006e-04 9.99042194e-01]
[ 1.46187658e-04 9.99853812e-01]
[ 3.77475828e-15 1.00000000e+00]
[ 1.42848622e-10 1.00000000e+00]
[ 1.24941870e-03 9.98750581e-01]
[ 3.32650120e-04 9.99667350e-01]
[ 2.17723400e-03 9.97822766e-01]
[ 1.89163614e-04 9.99810836e-01]
[ 4.11886369e-06 9.99995881e-01]
[ 5.70938914e-05 9.99942906e-01]
[ 2.22044605e-16 1.00000000e+00]
[ 2.95666394e-04 9.99704334e-01]
[ 3.32650120e-04 9.99667350e-01]
[ 2.17723400e-03 9.97822766e-01]
[ 0.00000000e+00 1.00000000e+00]
[ 9.85374946e-05 9.99901463e-01]
[ 0.00000000e+00 1.00000000e+00]
[ 9.57806006e-04 9.99042194e-01]
[ 4.94149421e-03 9.95058506e-01]
[ 0.00000000e+00 1.00000000e+00]
[ 8.55780967e-06 9.99991442e-01]
[ 1.89548377e-11 1.00000000e+00]
[ 0.00000000e+00 1.00000000e+00]
[ 7.56407540e-07 9.99999244e-01]
[ 2.22044605e-16 1.00000000e+00]
[ 5.44809459e-04 9.99455191e-01]
[ 4.04121181e-14 1.00000000e+00]
[ 3.44875017e-10 1.00000000e+00]
[ 2.84827384e-09 9.99999997e-01]
[ 2.18720153e-10 1.00000000e+00]
[ 3.10862447e-15 1.00000000e+00]
[ 0.00000000e+00 1.00000000e+00]
[ 2.32948771e-10 1.00000000e+00]
[ 2.22969262e-05 9.99977703e-01]
[ 1.98172909e-05 9.99980183e-01]
[ 5.53108596e-04 9.99446891e-01]
[ 0.00000000e+00 1.00000000e+00]
[ 2.22044605e-16 1.00000000e+00]
[ 5.70938914e-05 9.99942906e-01]
[ 1.69103823e-04 9.99830896e-01]
[ 0.00000000e+00 1.00000000e+00]
[ 9.86461801e-10 9.99999999e-01]
[ 5.44809459e-04 9.99455191e-01]
[ 4.94149421e-03 9.95058506e-01]
[ 2.66453526e-15 1.00000000e+00]
[ 1.50285909e-05 9.99984971e-01]
[ 3.32650120e-04 9.99667350e-01]
[ 0.00000000e+00 1.00000000e+00]
[ 1.56805513e-03 9.98431945e-01]
[ 1.00059923e-07 9.99999900e-01]
[ 2.55741846e-05 9.99974426e-01]
[ 3.80312604e-09 9.99999996e-01]
[ 2.17723400e-03 9.97822766e-01]
[ 1.93556826e-03 9.98064432e-01]
[ 2.17723400e-03 9.97822766e-01]
[ 4.30766534e-14 1.00000000e+00]
[ 3.32650120e-04 9.99667350e-01]
[ 2.17723400e-03 9.97822766e-01]
[ 0.00000000e+00 1.00000000e+00]
[ 0.00000000e+00 1.00000000e+00]
[ 5.18792508e-05 9.99948121e-01]
[ 2.32902586e-12 1.00000000e+00]
[ 9.57806006e-04 9.99042194e-01]
[ 0.00000000e+00 1.00000000e+00]
[ 9.57579875e-05 9.99904242e-01]
[ 1.56805513e-03 9.98431945e-01]
[ 0.00000000e+00 1.00000000e+00]
[ 1.24941870e-03 9.98750581e-01]
[ 1.80510660e-04 9.99819489e-01]
[ 0.00000000e+00 1.00000000e+00]
[ 5.19896576e-04 9.99480103e-01]]
第十一步:数据预测
# a. 预测数据格式化(归一化)
X_test = ss.transform(X_test) # 使用模型进行归一化操作
# b. 结果数据预测
Y_predict = re.predict(X_test)
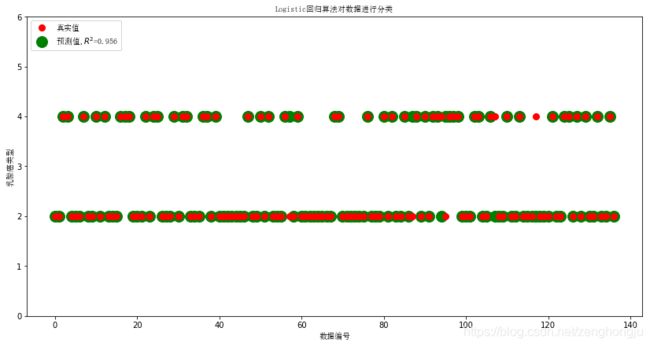
第十二步:画图
x_len = range(len(X_test))
plt.figure(figsize=(14,7), facecolor='w')
plt.ylim(0,6)
plt.plot(x_len, Y_test, 'ro',markersize = 8, zorder=3, label=u'真实值')
plt.plot(x_len, Y_predict, 'go', markersize = 14, zorder=2, label=u'预测值,$R^2$=%.3f' % re.score(X_test, Y_test))
plt.legend(loc = 'upper left',prop=my_font)
plt.xlabel(u'数据编号', fontsize=18,fontproperties=my_font)
plt.ylabel(u'乳腺癌类型', fontsize=18,fontproperties=my_font)
plt.title(u'Logistic回归算法对数据进行分类', fontsize=20,fontproperties=my_font)
plt.show()