《Production Matching for Large Learning Systems》 第二章节翻译

第二章 基础Rete算法

由于本论文的大部分工作都以Rete匹配算法为基础，所以本章主要描述Rete算法。不幸的是，大多数文献中对Rete算法的描述都不够特别明晰，这也许是Rete被冠以极度难懂的帽子的原因（Perlin，1990b）。为了扭转这种形势，本章将以教程的形式描述Rete，而不是简略地回顾一下或引导读者去看其它完整描述此算法的文献资料。我们首先大体上看一下Rete，然后讨论数据结构和常见的实现方式。本文中会给出主要数据结构和程序的伪代码，这可以给想在自己系统中实现Rete算法或变体的读者们一个指导。已经熟悉Rete或者只是想了解本论文研究贡献的人可以跳过本章。2.6节及后面的章节讨论Rete的高级特性，这几节不会影响论文其余大部分内容的理解，所以，第一次阅读时可以跳过这几节。

我们在开始讨论Rete之前，先回顾下一些基本的术语和表示方法。Rete（通常发音为REET或者REE-tee，源自拉丁语中网络的意思）涉及生产区（Production Memeory，简称PM）和工作区（Working Memory，简称WM）。它们两个会随着时间逐渐地改变。WM是当前系统状态下的“事实（Fact）”集合–外部世界的状态 和/或 系统自己内部要解决问题的状态。WM中每个元素被叫做工作区元素（Working
Memory Element,简称WME）。举个例子，在积木世界系统里，工作区（WM）可能由下面的WMEs（记为w1-w9）组成：

w1:(B1 ^on B2)
w2:(B1 ^on B3)
w3:(B1 ^color red)
w4:(B2 ^on table)
w5:(B2 ^left-of B3)
w6:(B2 ^color blue) 
w7:(B3 ^left-of B4)
w8:(B3 ^on table) 
w9:(B3 ^color red) 

为了简化我们的描述，我们会假设WMEs是三元组的形式，把它们写成(identifier ^attribute value)。“identifier",“attribute”,“value”，对匹配器来说没有特殊的含义。我们有时把”identifier"缩写成id，”attribute“缩写成attr。我们会把这部分作为一个WME的三个域，
比如，WME(B1 ^on B2)中id字段的值是B1。每个域中只包含一个符号。符号的唯一约束是它们都必须是常量：WMEs中不允许有变量。Rete不要求特殊表示–众多的Rete版本中支持其它已经实现的表示，我们会在2.11节讨论这些。在这里我们选择该特殊形式是因为：

• 它非常简单
• 对WMEs这种形式的约束并没有带来表示能力的丧失，其它更少约束的表示能够被直接地、机械地转换成这种形式，我们会在2.11节看到这些约束。
• 本论文中稍后提到的试验系统使用这种表示

生产区（PM）是一组作业（例如，rules）。一个作业被指定为一组条件（conditions）,被称为左则区域（left-hand side，LHS），
和一组行为（Actioins），被称为右则区域（Right-hand Side,RHS）。作业通常写成下面的形式：

 (name-of-this-production
   LHS  /* 一个或多个条件*/
  -->
   RHS  /* 一个或多个行为 */
 )

匹配算法通常会忽略行为只处理条件。匹配算法作为一个模块或者子程序被整个系统调用，以确定哪个作业的所有条件都是满足的，然后系统的一些其它部分会执行这些作业的行为。因此，本章将会聚焦在条件上。条件可以包含变量，我们把它写在尖括号里，比如：。在我们的
”积木世界“例子中，下面的规则可以被用作的查找红方块左边的两个（或更多）方块：

(find-stack-of-two-blocks-to-the-left-of-a-red-block
  (x ^on y)
  (y ^left-of z)
  (z ^color red)
 -->
  ... RHS ...
)

如果一个作业的所有条件均在当前工作区中命中了WME，并且条件中的所有变量始终绑定，那么这个作业被称作匹配当前工作区。例如，上面的的作业匹配上了上面的工作区，因为它的三个条件被w1、w5、w9分别匹配上，第一个和第二个条件中的绑定到B2，第二和第三个条件中的绑定到B3。配算法的工作是确定系统中的哪个作业匹配上当前的工作区，并且对每一个匹配，确定哪个WME匹配到了哪个条件。请注意既然我们假设WMEs都是三元组，我们也能假设条件有同样的形式–一个非该形式的条件永远不会匹配上任何WME，也就是说它是无用的。

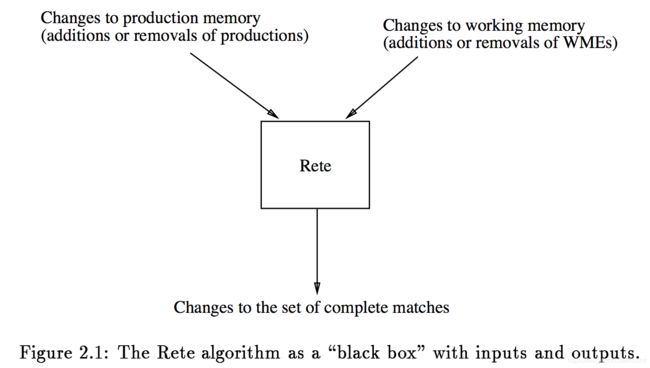
如图2.1所示，Rete被视作一个黑盒子。作为输入，它获取对当前工作区的变更信息（例如，增加WME）或者一组作业（例如，增加作业）。每次它被通知其中一个变化，匹配算法必须输出对匹配作业集的所有改变（比如，现在作业…匹配上了这些WMEs）。

2.1 概览

我们开始对Rete做一个简短的概览。如图2.2所示，Rete用一个数据流网络表示作业的条件。这个网络有两部分组成。Alpha部分执行WME中的常量测试（测试像red和left-of这样的常量标识）。它的输出被存储在alpha寄存器（AM），AM持有通过常量测试的WME集合。例如，在图示中，第一个条件( ^on )的AM，持有属性域包含符号on的WMEs。

alpha网络的实现在2.2节讨论。网络的beta部分首要包含join节点和beta寄存器（随后我们讨论几种其它的节点类型）。Join节点在两个条件变量绑定时 执行变量的一致性测试。Beta寄存器保存部分作业的实例（例如，匹配部分条件而非全部条件的WME组合）。这部分实例被称作tokens。

严格地说，在Rete的大部分版本中，alpha网络不仅执行常量测试并且也执行内部条件变量绑定一致性测试，此时一个变量在一个单独的条件中出现多于一次，比如，( ^self )。这样的测试在Soar中很少见，因此我们不在这里做过多的讨论。同时，注意测试实际上可以是任何布尔值的函数。在Soar中，大部分测试是相等测试（检查一件事件是否等于另外一件），因此我们在这里主要侧重在这种情况。无论如何，Rete的实现通常至少支持简单的条件测试（大于，小于，等等），一些版本允许任意用户自定义的测试。任何实现中，基本思路是alpha网络执行包含单个WME的所有测试，而beta网络执行包含两个或两个以上WME的测试。

把Rete算法和关系数据库进行下类比，也许对我们的理解是有帮助的。把当前的工作区（WM）当作一个关系表，每条作业当作一个查询。一个条件中的常量测试表示在WM表上作SELECT操作。对应于系统中的每一个不同的条件$c_i$，均有一个alpha寄存器（AM）存储SELECT的结果$r(C_i)$。现在，用$P$表示包含条件$c_1,...,c_k$的作业，$P$和当前工作区的匹配结果（如果P有任何的匹配）表示为$r(c_1)\&...\&r(c_k)$ ,JOIN操作是在所接受的参数上执行绑定功能的一致性检查。rete网络的beta部分中的join节点执行这些join操作，同时每个beta寄存器存储其中一个中间join的结果 $r(c_1)\&...\&r(c_i)(i<k)$。

无论何时，如果工作区发生变更，我们要更新这些SELECT和JOIN结果。步骤如下：工作区变更通过alpha网络被发送出去，同时相应的alpha寄存器被更新。然后这些变更被传递给相连的join节点，并激活这些节点。如果任何新的部分实例被创建，他们被添加到相应的beta寄存器，然后被向下传递到网络的beta部分，激活其它的节点。每当传递达到网络的最底层，它表明一条作业的条件被完全匹配到。这个通常靠在网络底层定义一个（p-node）的特殊节点来实现。每当p-node被激活，它意味着一个新的发现匹配完成（在一些系统相关的方法）。

Rete算法的大部分代码是由处理各种节点激活的程序组成。一个alpha寄存器节点的激活靠添加一个给定的WME到寄存器来处理，然后传递WME到寄存器的后继（successors）（Join节点会连接它）。相似地，beta寄存器节点的激活靠添加一个给定的token到寄存器来处理,然后把它传递到该节点的子节点（join节点）。总的来说，beta网络中从一个节点到另外一个节点的激活被称作左激活（left activation），来自alpha寄存器的节点的激活被称作右激活（right activation）。因此，一个join节点有两种类型的激活：当一个WME被添加到它的alpha寄存器时的右激活，和一个token被添加到beta寄存器时的左激活。左右join节点激活通常在两个不同的程序里实现，但在这两种情况下，都搜索节点的另一个寄存器是否存在和新元素有同样变量绑定的元素，如果有发现，它们将被传向join节点的子节点。

为了激活一个给定的节点，那么我们使用一个程序调用。这个特殊的程序依赖于节点的类型，比如，beta寄存器节点的左激活被一个程序处理，join节点的左激活被另外一个不同的程序处理。为了从某一节点传递数据流到它的后继节点，我们迭代这些后继节点并且为每个节点调用适合的激活程序。我们靠查找节点的类型来确认哪一个程序是适合的：我们使用switch case表达式通过于节点类型选择不同的分支，每个分支调用一个不同的程序，或者我们通过一个根据节点类型进行索引的跳转表来作程序调用。（为了效率有些编译器把switch表达式转成跳转表）。

Rete有两个重要的特性使之比原生匹配算法要快的多。第一个是状态保存。每一次对WM的变更，匹配的状态（结果）被保存在alpha和beta寄存器。在WM再次变更后，很多或大部分结果通常是没有变化的，而Rete靠维护WM变化时的不变的结果避免了很重复计算。（Rete为这样的系统而设计：在连续匹配的规则上只有很少的WME需要变更。Rete的状态保存在WME每次都改变的系统中不是很有用）。

Rete的第二个重要的特性是在具有相似条件的作业间的节点共享。不同类别的共享出现在网络的不同部分。在alpha网络中的共享，如2.2节讨论的。对alpha网络的输出，当两个或以上的作业有同样的条件，Rete只使用一个AM来存储这些条件，而不是为每一个条件创建重复的寄存器。例如，在图2.2(a)中，C3的AM被作业P1和P3所共享。此外，在网络的beta部分，当两个或以上的作业前几个少量条件相同时，同一节点将被用来匹配这些条件。这避免了这些作业的重复匹配。在图示中，三个作业具有相同的前两个条件，二个作业有相同的前三个条件。因为这种共享方式，beta部分构成了一棵树。

可以使用解释型语言或编译型语言实现Rete算法。在解释版本中，网络的描述仅被简单地存储为解释器可以执行的数据结构。在编译版本中，网络不是被显式地表示，而是被一个方法(function)集合代替，通常一个node会有一个或两个方法。比如，一个解释版本要提交一个通用的"left-activation-of-join-node"程序到一个特殊的join节点（靠把程序的指针指向节点的数据结构），编译版本是使用一段为这个特殊节点创建的一段程序，编译器是基于 解译器生成的关于这个特殊节点的程序 上生成的这段程序。（本章会描述通用解释器程序）。编译版本的优势当然是更快的速度。它的缺点一是需要更大的存储空间（一个节点的编译程序通常比解释的数据结果占用更多的空间），二是运行时程序很难添加或者删除（修改编译过的代码比修改一个解释的数据结构难多了–尽管至少一个编译版本解决了这个问题）。

在本章的剩余部分，我们将更深入地描述Rete，给出它的基本数据结构和程序的高级伪代码。这些伪代码会一节一节地给出，为了支持后续章节中要讨论的工作，后面的章节中可能会修订之前章节中的伪代码。完整版本的伪代码，以及一些在后面章节介绍的重要改进，均会放在附录A里。

一个系统的Rete模块有四个入口点：add-wme，remove-wme，add-production和remove-production。我们先从add-wme的调用开始讨论：2.2节alpha网络做什么，2.3节描述alpha和beta寄存器节点做什么，2.4节描述join节点做什么。我们将在2.5节讨论remove-wme，2.6节讨论add-production和remove-production。接下来我们将讨论一些Rete更复杂的特性：2.7节展示了如何处理否定条件（测试WME的不存在），2.8节展示否定结合（测试WME组合的不存在）如何被处理的。然后我们在2.9节给出几种实现说明，并在2.10节纵览近年来关于Rete算法的一些其它优化方法。最后，在2.11节讨论一下Rete算法的普遍性，包含它对更少WME限制表示的适应性。

2.2 Alpha网络实现

当一个WME被添加到工作区后，alpha网络会在上面执行必要的常量（或内在条件）测试并且把它存储到一个或更多合适的alpha寄存器。这里有几种发现合适alpha寄存器的方法。

2.2.1 数据流网络

原始的并且可能是最直接的一个方法是用一个简单的数据流网络。图2.3给出了一个只有10个条件（C1-C10）的小型规则系统的网络示例。这个网络的构成如下所述。对每一个条件，让$T_1，...，T_k$代表它的常量测试，可以按任何顺序排列（通常的方式是按源文本中条件的顺序从左到右排列）。从顶部的（根）节点开始，我们对应于$T_1,...,T_k$构建k个相应节点，组成一个路径。这些节点在文献上通常被称作常量测试或者单输入节点。当我们构建这个路径时，在条件允许时，我们会共享（比如，重用）已经存在的、包含同样的测试的节点（对其它节点来说）。最后，我们把这个条件的alpha寄存器当作$T_k$的节点输出。

请注意这个构建仅关注条件中的常量，同时忽略变量名称。因此，在图2.3中，条件C2和C10即使包含不同的变量名称还是会共享一个alpha寄存器。同时请注意一个条件也可能根本不包含常量测试（例如，图中的C9），在这种情况下它的alpha寄存器就是alpha网络中根结节的子节点。

这些节点其实是一个数据结构：包含了结节测试所需的信息，节点输出的AM，一组子节点（其它常量测试节点）：

structure   constant-test-node:
 field-to-test:"identifier","attribute","value",or "no-test"
 thing-the-field-must-equal:  symbol 
 output-memory:alpha-memory or   nil 
 children:  list  of constant-test-node
end 

（“no-test”会被用在根节点）当一个WME被添加到工作区，我们仅仅把它填进数据流网络的项端：

procedure  add-wme(w:WME) {dataflow version}
 constant-test-node-activaction (the-top-node-of-the-alpha-network,w) 
end 

procedure  constant-test-node-activation (node: constant-test-node; w: WME)
  if  node.eld-to-test != 'no-test'   then 
       v <-- w.[node.field-to-test]
  if  != node.thing-the-field-must-equal   then 
    return  ffailed the test, so don't propagate any furtherg
  if  node.output-memory !=   nil then 
       alpha-memory-activation (node.output-memory, w) fsee Section 2.3.1g
  for each  c   in  node.children   do  constant-test-node-activation (c, w)
end 

上面的描述假设所有的测试都是关于常量的相等测试。像前面所提及的，靠alpha网络执行的测试不限于相等测试。比如，一个条件也许要求在WME中的某个属性有一个比7大的数值。为了支持这样的测试，我们可以扩展constant-test-node数据结构来包括需要被执行的测试的定义，并且相应地修改constant-test-node-activation程序。

2.2.2 带哈希的数据流网络

Alpha网络的上述实现是简单且直接的。但是，在大型系统中它有一系列的缺点。读者也许已经从图2.3中猜到了，当一个节点的输出很大(多)时它带来了很多的浪费。在图中，attr=color?这个节点有5个子节点，并且它们的测试是互不干扰的。当一个WME经过attr=color?测试时，5个以上的测试被执行，每个子节点一次，最多只有一个节点可能执行成功。当然，一个节点所包含的相互独立的子节点的个数并没有限制，所以随着系统学习新的规则，子节点的个数也会增长。室内装饰的专家系统可能会学习越来越多的特殊颜色的名称。一个药物学习系统也许要学习越来越多的疾病。随着系统的增长，在Alpha网络中这些点上，像这样大量“浪费”的工作也会随之增长，因此匹配器会急速变慢。

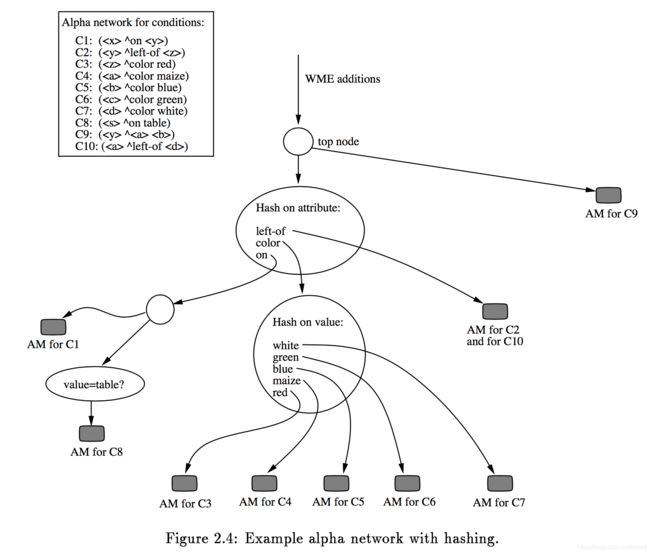
这个问题显而易见的解决方案是用一个特殊的节点来代替网络中这个有巨大输出结果的节点，这个特殊节点使用一个hash表（或者平衡二叉树）去确定激活需要哪条路径来继续向下。在上面的例子中，直接使用hash去查找匹配WME属性值的节点来替代激活5个子节点。事实上，由于hash能够高效地执行同样的测试，子节点能够被消除（省略，不使用）。图2.4给出了使用hash技术的结果。扩展前面的伪代码去处理这些hash表很简单。

2.2.3 hash表查找方法的详细说明

既然WMEs被要求是三元组，有一个仅靠几个hash表查询就可简单优雅的去实现大部分alpha网络的方法。

假设此时所有的常量测试都是等于测试–比如，没有大于、不等于或者其它特殊的测试。那么我们能够得到下面的观察：给出任意一个$WME$，$WME$能够进入的最多只有8个alpha寄存器。这是因为每个alpha寄存器都有这样的范式（test-1 ^test-2 test-3)，这里每三个测试要么是特定常量符号的等于测试，要么不关心，我们用“*”来标记。如果一个$WME$ $w$=(v1 ^v2 v3)进入到alpha寄存器a中，那么a必定是下面八种范式中一其中之一：

(* ^* *)
(* ^* v3)
(* ^v2 *)
(* ^v2 v3)
(v1 ^* *)
(v1 ^* v3)
(v1 ^v2 *)
(v1 ^v2 v3)

仅有8种方法能够生成(v1 ^v2 v3)匹配的条件。因此，给定一个WME $w$，去确定$w$应该添加到哪个alpha存储，我们仅需检查这8种可能哪个会真正在系统中。（既然不是任何alpha寄存器都会对应有测试和*的组合，一些情况也许根本不会出现）我们在hash表中存储指向alpha寄存器的指针，使用将被用做测试的值做为索引。执行alpha网络就变成了8种hash表查询的简单匹配：

procedure add-wme (w: WME) fexhaustive hash table versiong
  let v1, v2, and v3 be the symbols   in the three fields of w
  alpha-mem  <-- lookup-in-hash-table (v1,v2,v3)
  if alpha-mem != \not-found" then alpha-memory-activation (alpha-mem, w)
  alpha-mem  <-- lookup-in-hash-table (v1,v2,)
  if alpha-mem != \not-found" then alpha-memory-activation (alpha-mem, w)
  alpha-mem  <-- lookup-in-hash-table (v1,,v3)
  if alpha-mem != \not-found" then alpha-memory-activation (alpha-mem, w)
  ...
  alpha-mem <--  lookup-in-hash-table (,,)
  if alpha-mem != \not-found" then alpha-memory-activation (alpha-mem, w)
end

上面算法的优雅取决于两个假设：WMEs的三元组表示 和 没有不等于的测试。第一个假设能够比较轻松的理解：为了处理r元组的WMEs，我们能够使用$2^r$次hash表查询。当然，只有在$r$非常小时才能工作的很好。有两个方法去消除第二个假设：

• 可以用上面2.2.1章节中描述的小数据流网络形式来表示hash表查询的结果，而不是用alpha寄存器。所有常量等于测试用hash处理，而其它测试用像之前的常量测试节点来处理。重要的是，使用2.2.1章节数据流网络的查询结果，移动所有等于测试到网络的上半部分其它测试到下半部分，然后用8种hash查询替换掉上半部分

• 用网络的beta部分代替alpha部分来处理不等于测试。当然，在beta部分而不是alpha部分执行一些常量（或内置条件）测试对于Rete的实现也是可能的。这导致alpha网络几乎不再重要，并且丝毫不会增加多少beta网络的复杂性。然后，当不同规则有同一个条件时它减少了这些测试被共享的可能性。(这个正是该理念中实现的途径）。

不管是2.2.2章节中的数据流加hash的实现还是2.2.3章节中的穷举hash表查询实现，alpha网络都是非常高效的，工作区的每次变更都几乎是常量时间运行。网络的beta部分的消耗在Sora系统中占了大部分，并且之前的研究已经在OPS5中被证实。本章大部分（并且该理论的大分）因此也会处理网络的beta部分。

2.3 存储节点实现

现在我们讨论一下alpha和beta存储节点的实现。回忆一下alpha寄存器存储WMEs集合，beta寄存器存储token集合，每一个token代表一个WMEs的序列–具体来说是：满足某些作业前k个条件（具有一致变量绑定）的k个WMEs的序列。

有各种实现寄存器节点的方法。我们可以根据两个标准对实现做分类：

• （WMEs或tokens的）集合是如何构成的？
• 一个token–WMEs的序列–如果表示的？

对第一个问题，最简单的方法不需要在原有集合上加强加一个特殊的结构，我们仅使用列表来表示，并且元素是无序的。但是，我们在join操作时，通常可以通过在寄存器上增加一个索引结构在来增加效率。究竟如何，考虑一下我们之前的例子：

(find-stack-of-two-blocks-to-the-left-of-a-red-block
(x ^on y) /* C1 */
(y ^left-of z) /* C2 */
(z ^color red) /* C3 */
-->
 ... RHS ...
)

这个单条作业的Rete网络如第10页的Figure2.2（b）所示，当一个新的WME(B7 ^color red)添加到工作区（WM）时，它将会被添加到C3的AM中，且最底部的join node将会被右激活。join node严格检查是否有匹配上前两个条件（C1，C2）且 右值（right-of，相对于规则中的left-of来说）为的匹配结果。为了达到上面的目的，join node会在它的beta memory(与此join node 相连接的BM)中搜索是否有某个token(这里应该是批一个token，即某个WME实例)在属性上绑定了B7。如没有索引的话，这个搜索需要在整个beta memory上迭代一遍；但是，如果beta memory中的tokens已经建立了绑定到的索引的话，这个搜索将会非常快。相似的，当一个新的token被添加到beta memory中时，join node会被左激活，且会在它自己的alpha memory中搜索是否有值满足条件的WME；这个操作也可以通过对alpha memory建立索引而提速。

hash table是为memory node建议索引最常见的一种方法。（树结构是另一种方法，但是在Rete算法的实现中应用的不是很广，且（Bara chini， 1991）发现，通常情况下，hash table的表现比树结构要好）。但是在每个memory node中建立hash table会引起一个问题：hash table的大小怎么选择？一个node的tokens或WMEs会随着时间而增长。如果hash table总是很小，那么我们将会有很多冲突，这将会减少hash的效率。如果hash table总是很大，那么，当node只有很少或没有 tokens或WMEs，我们会浪费很多内存。我们可在增加或删除数据时动态的调整hash tabel的大小，但这需要在一个很简单的程序里放入一个很复杂的代码。

通常这个冲突的解决办法是把所有beta memory中的tokens都索引到一个大的全局hash table中，把所有alpha memory中的WMEs索引到另一个大的全局hash table中，从而使每个node不再使用分割的hash table。全局hash table的大小是事先设置好的，它的值会很大（也许有几千个箱）。哈希函数可以接受token和WME的绑定变量（例如：上文提到的），也可以接受node本身(eg. an identification nmber unique to the particular memory node containing the token or WME, or the virtual memory address of that node)。这个方法的目的是最小化哈希冲突（碰撞）
（1）如果我们固定memory node，改变变量的绑定，那么散列函数结果应该均匀分布在各个桶中。
（2）如果我们固定变量绑定，改变memory node，那么散列函数结果应该同样均匀分布在各个桶中。

如上所述，使用索引后的内存在连接操作时可以极大的减少所有时间，提高匹配器的速度。尽管这种做法有两个缺点：首先，这增加了向memory node中增加或删除item时的时间，因为需要更新索引表。其次，它可以减少共享，有时必须构建“重复”的内存节点，每个节点都存储相同的信息，但以不同的方式对其进行索引，例如，考虑如下场景，如果我们向上述内容添加第二个略有不同的作业会发生什么：

(slightly-modified-version-of-previous-production
(x ^on y) /* C1 */
(y ^left-of z) /* C2 */
(y ^color red) /* C3, but tests  instead of  */
-->
 ... RHS ...
)

对于这个作业，我们想要把表示匹配前两个条件的tokens通过它们绑定的变量建立索引，而不是它们绑定的变量。如果memory node都不建立索引，而是简单的无序列表，那么两个作业能共享一个’memory node’来保存前两个匹配上的条件。在有索引时，我们需要两个memory node而不是一个(或维护两个不同索引的一个节点)。由于这两个小开销，索引在一些系统中也不是很合适，特别是那些memory中不会包含很多项目的系统。

不管这些潜在的缺点，实践中的经验结果表明，使用hash的寄存器比没有索引的寄存器提升很多。（Gupta et al.,1988）发现在几个OPS5系统中靠1.2-3.5中的一个因素加速了匹配算法，并且 （Scales，1986）提道了1.2-1.3的一个因素对Soar系统。

注意，我们并不能总是找到绑定值可以在memory建立索引的变量。例如，有时一个条件与所有之前的条件是完全无关的：

  ( x ^on y)  /* C1 */
  ( a ^left-of b ) /* C2 */

在这个例子中，在C2的join节点之前索引beta寄存器没有意义，因为C2没有测试任何在C1中使用过的变量。像这些的案例，我们只是简单地使用一个未索引的memory node。

现在转到第二个问题–一个token（WMEs的序列）是如果表示的？–这里有两种主要的可能。一个序列可以被一个数组（数组形式的token）或者靠一个列表（列表形式的token）所表示。由于数组能够提供直接访问序列中所有元素的优势–给定$i$，我们能在常数时间内找到第i个元素–而一个列表为了找到第i个元素，需要循环前i-1个元素。因此，使用数组看起来是显而易见的选择。

然而，数组形式的tokens，能导致很多信息冗余存储，因此会使用更多的空间。为了弄明白为什么，注意到每一个beta寄存器节点存储一个作业中的前i>1个条件，另一个beta寄存器节点–它的祖父（跳过介于中间的join节点–存储前i-1个条件的匹配
结果。如果$(w_1,...,w_i)$表示对前i个条件的匹配，那么必定有一个对前i-1个条件的匹配。这意味着在较低的beta寄存器里的任意token能够被简洁地表示为$(parent,w_i)$对，在这里parent表示前驱前beta memory node中表示i-1个WMEs的token。如果我们在所有的beta寄存器里使用这个技术，那么每个token实际上变成了一个link-list，靠$prent$指针连接，表示一个反序的WME序列，$w_i$在列表的头部，$w_1$在尾部。同样地，我们使最上面的beta寄存器（仅表示一个WME的序列）里的token的父节点指向dummy top token，它表示一个空的序列<>。注意到目前所有token的集合形成了一棵树，子节点指向父节点，并且根节点是dummy top token。

使用数组形式的tokens，表示前i个条件的token消耗O(i)的空间，而使用列表形式的tokens，每个token仅使用O(1)的空间。这能够节省大量的空间，特别是如果有作业有大量条件的时候。如一个有$C$个条件的作业，做一次完全的匹配，数组形式的tokens会至少使用
$1+2+...+C=O(C^2)$的空间，而列表形式的tokens只需要$O(C)$的空间。当然，使用更多的空间意味着使用更多的时间去填满空间。每当一个beta memory node被激活，会创建并且存储一个新的token。使用数组形式的tokens，在添加第i个元素前，需要从上面循环拷贝i-1个元素。使用列表形式，创建一个token不需要这种循环。

总结一下，使用数组形式的tokens比使用列表形式的tokens需要更多的空间，但在每个beta memory的激活上需要更多的时间来创建每个token。然而，对一个指定的序列元素它提供了比列表形式更快的访问速度。为执行变量绑定的一致性检查，在join节点激活时经常需要访问任意的元素。在所有系统上，两种表示并没有一种一定比另一种好。因此我们有一个折衷。在一些系统上，使用数组形式的tokens会因空间的原因而不可行–比如，一个作业有巨量的条件。通常来说，使用列表形式的tokens的选择，依赖于访问任意元素的成本有多高。一个系统使用越多的变量一致性检查，并且包含的变量相距越远（比如，两个变量出现在一条规则非常靠前和靠后的位置，相对出现在条件中的$C_i$和$C_{i+1}$位置），访问的成本越大，那么数组形式的token会快一点。

现在我们转到伪代码上。为了尽量保持简单，我们在伪代码中使用列表形式的tokens和未索引的memory node。随着进行的深入，我们会指出产生重要区别的地方（本论文的实际实现使用了列表形式的tokens和hash寄存器节点）。

2.3.1 alpha寄存器实现

一个WME只包含三个属性：

structure WME:
  felds: array  [1..3] of  symbol  
end

一个alpha寄存器一个WME的列表，外加一个继续者列表（join节点会依附于它):

structure alpha-memory:
  items:  list of WME
  successors:  list of rete-no de
end  

无论何时一个新的WME通过alpha网络的匹配并且到达一个alpha memory时，我们仅简单地把它添加到memory的其它WME的列表中，并通知每个相连的join节点：

procedure alpha-memory-activation (no de: alpha-memory, w: WME)
  insert w at the head of no de.items
  for each childin no de.successors  do right-activation (child, w)
end

2.3.2 Beta寄存器实现

如上所述，使用列表形式的tokens，一个token仅是一个数据对：

structure token:
  parent: token {points to the higher token, for items 1...i-1}
  wme: WME {gives item i}
end

一个beta memory node包含一个保存tokens的列表，及它的子节点（beta网络的其它节点）的列表。在我们给出它的数据结构之前，我们将要再次通过一个swich/case表达式或者一个根据被激活节点的类型而创建的索引跳转表对左右激活的程序进行调用。因此，给出一个节点（或者指向它的指针），我们需要能够确定它的类型。当记录多样时，这样表示节点将非常直接。（一个多样记录是指它能够包含任何不同属性集）。在网络的beta部分的每一个节点将会用一个rete-node结构来表示：

structure rete-node:
  type: “beta-memory", "join-node", or "p-node" {or other node types we'll see later}
  children: list of rete-node
  parent: rete-node {we'll need this "back-link" later}
   ...(variant part -- other data dep ending on no de type) . . .
end 

既然从现在开始我们描述节点的每一个特殊类型，我们只列出某类节点的数据结构类型的扩展信息；记住在beta网络的所有节点都有$type$,$children$和$parent$属性。并且，我们仅简单地用left-activation或者right-activation来表示合适的switch/case表达式或跳转表的使用。

现在重新回到beta memory node，一个beta memory node存储的唯一扩展信息是它包含的tokens列表：

structure beta-memory:
  items:  list of token
end  

无论何时，当一个beta memory被一个新的匹配（由一个存在的token和一些WME组成）所通知，我们创建一个token，把它添加到beta memory的列表中，并通知beta memory的每一个子节点：

procedure beta-memory-left-activation (node: beta-memory, t: token, w: WME)
  new-token = allocate-memory()
  new-token.parent = t
  new-token.wme = w
  insert new-token at the head of no de.items
   for each child  in node.children  do left-activation (child, new-token)
end

2.3.3 P节点实现

我们在这里提到作业节点(p-node)的实现是因为它在一些方面通常和memory node的实现很相似。p节点的实现在不同的系统是不同的，因此在这里我们的讨论尽量会通用一点，并且不会给出伪代码。一个p节点可以存储tokens，就像beta寄存器一样；这些tokens代表了对作业条件的完全匹配。（在传统规则系统中，在所有p节点
中的所有tokens集合被表示为冲突集(conflict set)）。在一个左激活中，一个p节点会构建一个新的toekn，或者是一个新的完全匹配的相似表示。然后它通过某种方式（系统独立）发出一个新匹配的信号。

总的来说，一个p节点包含作业对应的定义–规则名称，RHS动作，等。一个p节点也可以包含出现在作业中的变量名称的信息。注意，变量名称并没有在本章我们描述的任何Rete节点数据结构中提起过。这是刻意为之–当两条规则有同一基本形式但有不同的变量名称的条件时它使节点能够被共享。当变量名称被记在某处时，它可能需要靠查找带有变量名称的Rete网络来重新构建作业的LHS。重新构建LHS消除了保存LHS”原始拷贝“的需求，这种情况下我们需要随后检查作业。

2.4 Join节点实现

像在概述中提出的那样，当一个WME被添加到alpha memory时，与之相连接的join节执行右激活，当一个token添加到beta memory时，与之相连的join节点执行左激活。在上面的任一一种情况下，join节点都会在与之相连的另一个memory中查找和新元素一致的变量绑定。如果找到了一致的绑定变量，则它们将被传递到join节点的子节点。

一个join节点的数据结构必须包含指向它的两个memory node的指针（这样它们才能被搜索到），对任意绑定变量的一致性检查的定义，以及保存其子节点的列表。从数据到所有的节点（上文22页中rete的节点结构），我们已经有了子节点；而且，$parent$字段给了我们一个指向join节点beta memory（beta寄存器总是它的父节点）的指针。我们在join节点中需要两个额外的属性：

structure join-node:
  amem: alpha-memory {points to the alpha memory this node is attached to}
  tests:  list of test-at-join-node
end

test-at-join-node的数据结构中指定了两个 需要一致性绑定的变量的位置/下标，它们在绑定时的值必须相等：

structure test-at-join-node:
  feld-of-arg1: "identifier", "attribute", or "value"
  condition-number-of-arg2:**integer**
  feld-of-arg2:  "identifier", "attribute", or "value"
end 

Arg1是WME（alpha memory ）的三个属性之一，而arg2是$WME$中需要与之前作业中的条件所匹配的字段（比如beta寄存器中token的一部分）。举例来说，在我们的示例规则中：

 (find-stack-of-two-blocks-to-the-left-of-a-red-block
   (x ^on y)      /* C1 */
   (y ^left-of z) /* C2 */
   (z ^color red) /* C3 */
  -->
   ... RHS ...
  ),

对C3的join节点，为了检查z的一致性绑定，我们约束来自join节点的alpha memory的WME的id属性的内容必须等于匹配第二个条件的WME的value属性。这将会有$filed-of-arg1="identifier"$,$conditon-number-of-arg2=2$和$field-of-arg2="value"$
以右激活举例（当一个新WME $w$被添加到alpha memory时），我们遍历join结点的beta memory，找到所有的token $t$，$t$应通过$t$-vuersus-$w$的测试。
通过测试的$<t,w>$对被传递到join结点的子结点。相似的，对一个左激活来说（当一个token添加到beta memory），我们遍历alpha memory 找到所有的WME $w$，$w$ 应通过$t$-vuersus-$w$的测试。相同的，通过测试的$<t,w>$对被传递到当前结点的子结点。

procedure join-node-right-activation (node: join-node, w: WME)
  for each t in node.parent.items  do {"parent" is the beta memory node}
  if perform-join-tests (node.tests, t, w)  then
    for each child  in node.children  do left-activation (child, t, w)
end 

procedurejoin-node-left-activation (node: join-node, t: token)
  for each w in node.amem.items  do
  if perform-join-tests (node.tests, t, w)  then
     for each child  in node.children  do left-activation (child, t, w)
end  

function perform-join-tests (tests:list of test-at-join-node, t: token, w: WME)  returning boolean
   for each this-test  in tests  do 
     arg1 = w.[this-test.field-of-arg1]
     {With list-form tokens, the following statement is really a loop}
     wme2 = the [this-test.condition-number-of-arg2]'th element in t
     arg2 = wme2.[this-test.field-of-arg2]
      if arg1 != arg2  then return false
    return  true 
end  

我们注意到上面程序的几点。第一，为了能够在网络中最最顶端的join节点使用这些程序–如2.2章节所述，他们都是dummy top node的子节点–我们需要dummy top node来担当这些join节点的beta memory。通常我们会在dummy top node中维护一个dummy top token，这样，在迭代join-node-right-activation的程序中只处理一个事情（没有特殊情况）。第二，伪代码假设所有的测试都是测试两个属性的相等。可以简单的扩展test-at-join-node的数据结构和perform-join-tests程序去支持其它的测试（比如，测试一个属性是否小于另外一个）。大部分但不是全部Rete的实现支持这些测试。最后，伪代码假设alpha和beta寄存器没有任何索引，像上面2.3节讨论的那样。如果寄存器被建立了索引，那么上面的激活程序需要被修改，使用索引而不是简单迭代完所有memory node中的tokens或WMEs。例如，如果memory做了Hash，程序仅会在合适的hash桶中的tokens或WMEs上迭代，而不是memory中的所有tokens或WMEs。这能够显著地加速Rete算法。

2.4.1 避免重复Tokens

无论何时我们添加一个WME到一个alpha寄存器，我们右激活每一个附属到alpha寄存器的join节点。迄今为止，在我们的讨论中，一个非常重要的细节被遗漏了。join节点被右激活的序列是至关重要的，因为如果join节点以错误的顺序激活可能生成重复的token（在同一个beta memory中有两个或两个以上的token代表同一个WME序列）。

为了弄明白这是如何发生的，考虑一个LHS由下面三个条件开始的作业：

  (x ^self y)    /* C1 */
  (x ^color red) /* C2 */
  (y ^color red) /* C3 */
   ...           /* other conditions */

假设工作区最初只包含一个WME，匹配第一个条件：

  w1: (B1 ^self B1)

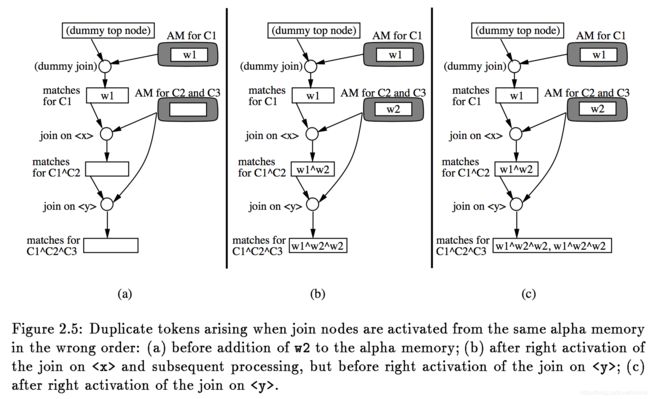
图2.5(a)展示了这种情况下的Rete网络，包括所有memory node的内容。注意到下面的alpha memory在这个作业中被两个条件C2和C3所使用。现在假设下一个WME被添加到工作区：

  w2: (B1 ^color red)

这个WME通过alpha网络的筛选，并且调用alpha-memory-activation程序添加w2到下面的alpha寄存器。我们把w2添加到寄存器的元素列表，然后我们不得不右激活两个join节点（一个连接在x的值上，一个连接在y的值上）。假设我们先右激活上面的一个（x的那个）。它搜索beta寄存器寻找合适的token，发现一个新匹配(w1,w2)，并把这个新匹配传递给它的子节点（保存有C1^C2匹配的beta memory）。它被添加到memory并传递给下面的join节点。现在该join节点搜索alpha memory寻找适合的WME–这时会发现我们刚添加到alpha memory中的w2 --并传递新的匹配(w1,w2,w2)到它的子结点。这次完成的处理是由上面的join节点触发。这个情况展示在图2.5(b)中。我们仍然不得不右激活下面的join节点。当我们右激活它时，它搜索beta寄存器寻找适合的token–这时会发现我们之前存入的。之后它传递这个新的匹配到它的子节点，没有识别这个是之前的一个重复匹配。最终的结果如图2.5©所示；注意最下面的beta寄存器包含了同一token的两份拷贝。

处理这个问题的一个办法是对beta memory node做重复token的检查。每次一个beta memory被激活，它会检查这个“新“的匹配实际上是否是寄存器中已存在的token。如果是，它将被忽略（比如，丢弃掉）。不幸地是，这将显著地拖慢beta memory激活的处理。

一个更好的避免拖慢的方案是以与上面例子不同的序列右激活join节点。在上面的例子中，如果我们先激活下面的join节点，不会有重复的token被生成（邀请读者检查这一点；核心的是当下面的join节点被右激活时，它的beta寄存器仍然是空的）。总的来说，右激活的解决方案依赖于它们的前驱节点；比如，如果我们需要从同一个alpha memory右激活join节点$J_1$和$J_2$，并且$J_1$是$J_2$派生的，那么我们在右激活$J_2$之前右激活$J_1$.我们添加一个WME到一个alpha memory的全部程序是：

1. 添加WME到alpha寄存的元素列表。
2. 右激活与之相连的join节点，后继节点在前驱节点之前。

另外一个方案是–在后继节点之前右激活前驱节点，然后添加WME到memory的元素列表–这也能工作。这个问题的完整讨论，请看(Lee and Schor,1992)。

当然，遍历Rete网络的每一个alpha memory激活，来查找先辈派生节点在join节点中的关系太笨了。相反的，我们可以在网络构建时提前检查这些，并确保alpha memory中的join节点列表是有序的：如果$J_1$和$J_2$都在列表上并且$J_1$是$J_2$的派生，那么$J_1$必须在$J_2$的前面。靠预先强制排序，我们避免后面在节点激活时的任何额外开销，并且避免生成任何重复的token。

我们将在第4章描述右断开连接（right unlinking）时回到这个问题，一个优化是join节点将被动态地加进和
移出alpha寄存器的列表。我们需要确保在进行此拼接时保持适当的顺序。

2.5 WME的移除

当一个WME从工作区删除，我们需要靠删任何包含WME的入口来相应地更新alpha和beta寄存器节点（和p节点中的token）中的条目。
有几种方法来实现这一点。

在最初的Rete算法中，删除本质上和添加的处理相同的。我们把这种方法叫作基于再匹配的删除(rematch-based removal)。基本
的思路是在解释器中的每个程序增加一个额外的参数，叫做标签(tag)，用来指定当前操作添加还是删除的标识。对于删除来说，
对alpha和beta寄存器节点的程序仅简单地从它们的寄存器中删除指定的WME或token来代替添加。然后程序调用他们的继承者，只是把
把它们作为一个添加，用delete做标签而不是add.Join节点的程序同样地处理添加和删除–在这两个案例中，他们用一致性变量
绑定在合适的寄存器中查找条目并且传递任何匹配（连同add/delete标签）到他们的子节点。因为这个基于再匹配的删除方法处理
删除和同一解释器程序处理添加大部分相同，因此它简单而优雅。

不幸地是，它也很慢，至少相对其它可能的方法。对基于再匹配的删除来说，既然同一个程序被调用并且每一个做了差不多的工作，
删除一个WME的代价和添加一个WME的代价其实是一样的。问题是在添加一个新的WME时没有信息可以随后在被删除这个WME时使用。
有至少三个方法可以在处理删除时使用这些信息。

在基于扫描的删除(scan-based removal中，我们不用在join节点重复做变量绑定一致性检查，代替的是仅简单地扫描它们的输出
寄存器（它们的子beta寄存器，p节点）来查找任何要被删除条目的入口。当一个join节点被右激活作一个WME w的删除时，它仅把w
传递到它的输出寄存器。寄存器查找token列表中最后一个元素是w的token，删除这些token，并发送这些删除到它的子节点。相似的，
当一个join节点被左激活作token t的删除时，它把t传递到它的输出寄存器。寄存器查找token列表中父亲是t的token，删除这些token，
并发送这些删除到它的子节点。注意查找token的父亲是t的这部分程序仅在使用列表形式时才高效而数组形式不行。在Soar系统中使用
基于扫描的删除比基于再匹配的删除效率提高28%；（Barachini，1991）则产使用轻微变量的这个技术比基于再匹配的删除效率提高10%。

也许处理删除的最快方法是提前精确地记下哪一个要被删除。这个直接的思路是基于列表的删除和基于树的删除的基础。这个思路
是在WME和token的数据结构增加额外的指针，因此当一个WME被删除时我们发现所有需要被删除的token–并且仅有这些需要被删除–仅
靠指针。

在由（Scales，1986）建议的基于列表的删除中，我们在每一个WME w中存储包含w的所有token列表。然后当w被删除，我们仅迭代这个
列表并删除在上面的每一个token。这个方法的缺点是需要大量额外的存储空间并且潜在的大量额外时间来创建一个token：一个新的
token（w,…,wi)必须被添加到每个w的列表中。然而，既然创建这个新otken无论如何都需要创建一个新的i个元素的数组，如果token
是用数组而不是列表来表示的话，那么空间和时间最多都会是一个常量因子。因此，基于列表的删除是那样的实现也许可以被接受。
论文中没有基于列表的删除的经验报道，因此它是否能在实际中工作的很好（或者甚至它曾被实现过）还不清楚。

在基于树的删除中，在每个WME w上，我们为最后一个w保存所有token的列表。在每个token t上，我们保存t的所有孩子的列表。这些
指向孩子token的指针允许我们在下面的beta寄存器和条件节点发现所有t的派生。（回头看下2.3章节中是用列表形式的token，这里的
token集合是一棵树）。现在当w被删除时，我们仅遍历子树（根token和它们的派生token的），并删除在它们里的一切。当然，所有这
些额外的指针意味着更多的存储空间，外加在WME被添加或token被创建之前的指针设置。然而，从经验上讲，在WME删除期间的时间节省
远胜提前设置指针的。当作者在Soar系统使用基于树的删除替换掉基于再匹配的删除后，匹配器提升了1.3倍的速度；（Barachini,1991)
在一个类OPS5的系统中估计有1.25倍的提升。

为了实现基于树的删除，我们每个WME的数据结构让它包括包含WME的所有alpha寄存器的列表，和把WME做为最后一个元素的所有token
的列表：

  structure WME {revisedfrom version on page 21}
    felds:array[1..3] of symbol
    alpha-mems:list of alpha-memory {the ones containing this WME}
    tokens:list of token {the ones with wme=this WME}
  end

token的数据结构被扩展到包含指向寄存器节点（我们会在下面的delete-token-and-descendents中使用）的指针和它的儿子们的列表：

  structure token {revised from version on page 22}
    parent: token {points to the higher token, for items 1...i-1}
    wme: WME {gives item i}
    node: rete-node {points to the memory this token is in}
    children:list of token {the ones with parent=this token}
  end

我们现在修改aplha-memory-activation和beta-memeory-left-activation程序提前设置这些列表。无论何时一个WME w被添加到alpha
寄存器a中，我们添加a到w.alpha-mems.

  procedure alpha-memory-activation (node: alpha-memory, w: WME)
  {revisedfrom version on page 21}
     insert w at the head of node.items
     insert node at the head of w.alpha-mems {for tree-basedremoval}
     for each child in node.successors do right-activation (child, w)
  end

相似地，无论何时一个新的token t=被添加到beta寄存器，我们添加tok到t.children和w.tokens。我们也在token上填充新节点
属性。为了简化我们的伪代码，定义一个helper函数make-token会方便一点，它构建一个新的token并初始化它的变量属性作为基于树
的删除的必备之选。虽然我们把这个作为一个独立的函数，但正常情况下它在代码使用inline会更高效。

  function make-token (node: rete-node, parent: token, w: wme)
  returning token
    tok =allocate-memory()
    tok.parent = parent
    tok.wme = w
    tok.node = node {for tree-based removal}
    tok.children =nil {for tree-based removal}
    insert tok at the head of parent.children {for tree-based removal}
    insert tok at the head of w.tokens {for tree-based removal}
    return tok
  end
  procedure beta-memory-left-activation (node: beta-memory, t: token, w: WME)
  {revised from version on page 23}
    new-token = make-token (node, t, w)
    insert new-token at the head of node.items
    for each childin node.children do left-activation (child, new-token)
  end

现在，删除一个WME，我们仅从包含它的每个alpha寄存器中删除它（这些alpha寄存器现在很方便在一个列表上）并调用helper子程序
delete-token-and-descendents去删除包含它的所有token（包含它的所有必要的根token也很方便在一个列表中）：

  procedure remove-wme (w: WME)
    for each am in w.alpha-mems do remove w from the list am.items
    while w.tokens !=nil do
       delete-token-and-descendents (the first item on w.tokens)
  end

注意w.tokens上使用的是while循环而不是for循环。for循环在这里并不安全，因为每次调用delete-token-and-descendents会破坏性
地修改w.tokens列表因为它要释放token数据结构使用的内存空间。for循环会持有一个指进它运行的列表的中间位置，并且这个指针
可能对这个破坏性的修改变得无效。

这个帮助类子程序delete-token-and-descendents删除一个token和它的整个派生树。为了简化，这里的伪代码是递归的；实际的实现
可以使用非递归树遍历方法会更快一点。

  procedure  delete-token-and-descendents (tok: token)
    while tok.children !=nil do
      delete-token-and-descendents (the first item on tok.children)
    remove tok from the list tok.node.items
    remove tok from the list tok.wme.tokens
    remove tok from the list tok.parent.children
    deallocate memory for tok
  end

2.5.1 列表实现