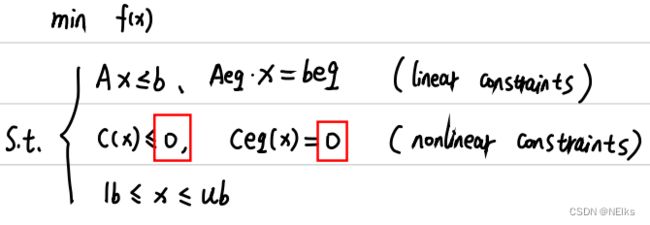数学建模:11 数学规划模型
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% 线性规划:
[x,fval] = linprog(c, A, b, Aeq, beq, lb, ub, x0);
% c是目标函数各个变量的系数组成的列向量
% lb是各个变量的下界组成的列向量
% 默认求的是目标函数的min、不等式约束是小于等于
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% 整数规划:
[x,fval] = intlinprog(c, intcon, A, b, Aeq, beq, lb, ub);
% intcon 行向量或数字,哪个变量要求是整数 就把它的下标加进来
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% 01规划:
% 在整数规划基础上 把lb ub限制为0 1
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% 非线性规划:
[x,fval] = fmincon(@fun, x0, A, b, Aeq, beq, lb, ub, @nonlfun, option);
% x0表示给定的初始值(用行向量或者列向量表示),必须得写
% option 表示求解非线性规划使用的方法
option = optimoptions('fmincon','Algorithm','interior-point') % 内点法
option = optimoptions('fmincon','Algorithm','sqp') % SQP(序列二次规划法)
option = optimoptions('fmincon','Algorithm','active-set') % active set(有效集法)
option = optimoptions('fmincon','Algorithm','trust-region-reflective') % trust region reflective (信赖域反射算法)
%%%%%%%%%%%%%% 使用蒙特卡罗的方法来找初始值(推荐)
clc,clear;
n=10000000;
x1=unifrnd(-100,100,n,1); % 生成在[-100,100]之间均匀分布的随机数组成的n行1列的向量构成x1
x2=unifrnd(-100,100,n,1);
fmin=+inf; % 初始化函数f的最小值为正无穷(后续只要找到一个比它小的我们就对其更新)
for i=1:n
x = [x1(i), x2(i)]; %构造x向量, 这里千万别写成了:x =[x1, x2]
if 约束条件1 & 约束条件1
result = 目标函数; % 如果满足条件就计算目标函数值
if result < fmin
fmin = result;
x0 = x;
end
end
end
%%%%%%%%%%%%%%%% fun.m
function f = fun(x)
% 目标函数:max f(x) = x1^2 +x2^2 -x1*x2 -2x1 -5x2
f = -x(1)^2-x(2)^2 +x(1)*x(2)+2*x(1)+5*x(2) ;
end
%%%%%%%%%%%%%%%% nonlfun.m
function [c,ceq] = nonlfun(x)
% 非线性不等式约束,多个要用列向量
c = [-x(1)^2+x(2)-x(3)^2;
x(1)+x(2)^2+x(3)^2-20];
% 非线性等式约束
ceq = [-x(1)-x(2)^2+2;
x(2)+2*x(3)^2-3];
end
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% 最大最小化模型:
[x,fval] = fminimax(@Fun, x0, A, b, Aeq, beq, lb, ub, @nonlfun, option);
% Fun是函数向量 Fun.m
function f = Fun(x)
a=[1 4 3 5 9 12 6 20 17 8];
b=[2 10 8 18 1 4 5 10 8 9];
% 函数向量
f=zeros(10,1);
for i = 1:10
f(i) = abs(x(1)-a(i))+abs(x(2)-b(i));
end
end
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% 多目标规划:
[x,fval] = fgoalattain(func,goal,weight,x0,A,b,Aeq,beq,lb,ub)
% 具体用法看后面的例子![]()
目录
概述
分类
线性规划
例题
非线性规划
例题
选址问题
国赛A题:飞行管理
整数规划
例题
背包问题
指派问题
钢管切割问题
最大最小化模型
例题
多目标规划模型
参考资料
概述
数学规划的目标:求目标函数在一定约束条件下的极值问题
组成:决策变量、目标函数、约束条件
分类
- 线性规划:目标函数和约束条件 均是 决策变量的线性表达式(单纯形法一定能解决线性规划,有唯一/多个解)
- 非线性规划:目标函数和约束条件 有一个是 决策变量的非线性表达式(需给定决策变量的初始值,只能求近似解)
- 整数规划:要求变量取整数
- 线性整数规划
- 非线性整数规划:目前没有准确解法,可用蒙特卡洛
- 01规划:整数规划的特例,只能取0/1
线性规划
参考:matlab线性规划--简单入门_老蔡的菜的博客-CSDN博客_matlab线性规划
其中的初始值x0只加快得到结果的速度,结果与x0无关
例题
Matlab线性规划实例_zz_Outlier的博客-CSDN博客_matlab线性规划例题
clear,clc
format long g %可以将Matlab的计算结果显示为一般的长数字格式(默认会保留四位小数,或使用科学计数法)
% (1) 系数向量
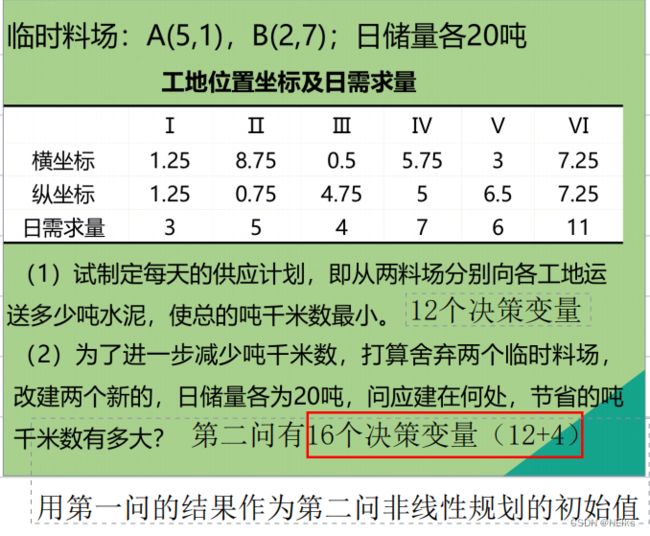
a=[1.25 8.75 0.5 5.75 3 7.25]; % 工地的横坐标
b=[1.25 0.75 4.75 5 6.5 7.25]; % 工地的纵坐标
x = [5 2]; % 料场的横坐标
y = [1 7]; % 料场的纵坐标
c = []; % 初始化用来保存工地和料场距离的向量 (这个向量就是我们的系数向量)
for j =1:2
for i = 1:6
c = [c; sqrt( (a(i)-x(j))^2 + (b(i)-y(j))^2)]; % 每循环一次就在c的末尾插入新的元素
end
end
% (2) 不等式约束
A =zeros(2,12);
A(1,1:6) = 1;
A(2,7:12) = 1;
b = [20,20]';
% (3) 等式约束
Aeq = zeros(6,12);
for i = 1:6
Aeq(i,i) = 1; Aeq(i,i+6) = 1;
end
% Aeq = [eye(6),eye(6)] % 两个单位矩阵横着拼起来
beq = [3 5 4 7 6 11]'; % 每个工地的日需求量
%(4)上下界
lb = zeros(12,1);
% 进行求解
[x fval] = linprog(c, A, b, Aeq, beq, lb)
x = reshape(x,6,2) % 将x变为6行2列便于观察(reshape函数是按照列的顺序进行转换的,也就是第一列读完,读第二列,即x1对应x_1,1,x2对应x_2,1)
% fval =
% 135.281541790676非线性规划
先用蒙特卡罗找到一个解,作为非线性规划的初始值 x0,matlab:fmincon
例题
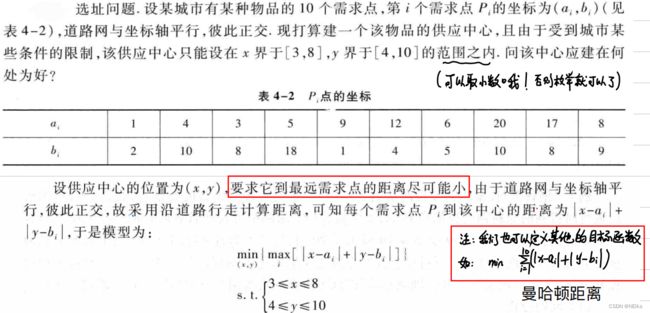
选址问题
国赛A题:飞行管理
详见pdf
整数规划
例题
背包问题
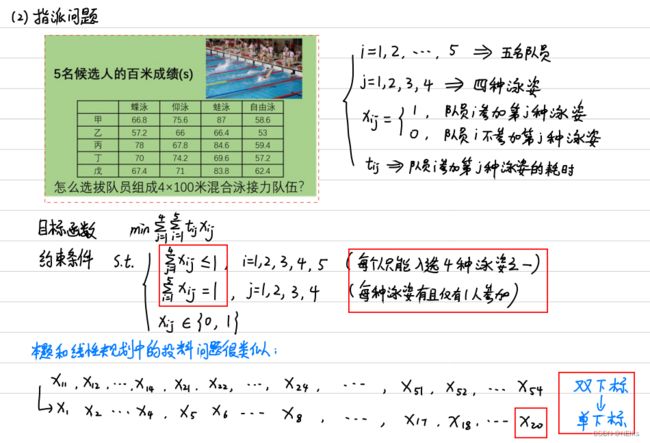
指派问题
%% 指派问题(选择队员去进行游泳接力比赛)
clear;clc
c = [66.8 75.6 87 58.6 57.2 66 66.4 53 78 67.8 84.6 59.4 70 74.2 69.6 57.2 67.4 71 83.8 62.4]'; % 目标函数的系数矩阵(先列后行的写法)
intcon = [1:20]; % 整数变量的位置(一共20个决策变量,均为0-1整数变量)
% 线性不等式约束的系数矩阵和常数项向量(每个人只能入选四种泳姿之一,一共五个约束)
A = [1 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0;
0 0 0 0 1 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0;
0 0 0 0 0 0 0 0 1 1 1 1 0 0 0 0 0 0 0 0;
0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 0 0 0 0;
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1];
% A = zeros(5,20);
% for i = 1:5
% A(i, (4*i-3): 4*i) = 1;
% end
b = [1;1;1;1;1];
% 线性等式约束的系数矩阵和常数项向量 (每种泳姿有且仅有一人参加,一共四个约束)
Aeq = [ 1 0 0 0 1 0 0 0 1 0 0 0 1 0 0 0 1 0 0 0;
0 1 0 0 0 1 0 0 0 1 0 0 0 1 0 0 0 1 0 0;
0 0 1 0 0 0 1 0 0 0 1 0 0 0 1 0 0 0 1 0;
0 0 0 1 0 0 0 1 0 0 0 1 0 0 0 1 0 0 0 1];
% Aeq = [eye(4),eye(4),eye(4),eye(4),eye(4)]; % 或者写成 repmat(eye(4),1,5)
beq = [1;1;1;1];
lb = zeros(20,1); % 约束变量的范围下限
ub = ones(20,1); % 约束变量的范围上限
%最后调用intlinprog()函数
[x,fval] = intlinprog(c,intcon,A,b,Aeq,beq,lb,ub)
% reshape(x,4,5)'
% 0 0 0 1 甲自由泳
% 1 0 0 0 乙蝶泳
% 0 1 0 0 丙仰泳
% 0 0 1 0 丁蛙泳
% 0 0 0 0 戊不参加钢管切割问题
这里用了枚举法:一根6.9m,只能切割出 2 根2.9m,所以2.9m枚举范围:[0, 2];同理2.1m:[0, 3];0.9m:[0, 6]
for i = 0: 2 % 2.9m长的圆钢的数量 最多只能切出2根
for j = 0: 3 % 2.1m长的圆钢的数量
for k = 0:6 % 1m长的圆钢的数量
if 2.9*i+2.1*j+1*k >= 6 && 2.9*i+2.1*j+1*k <= 6.9
disp([i, j, k])
end
end
end
end
c = ones(7,1); % 目标函数的系数矩阵
intcon=[1:7]; % 整数变量的位置(一共7个决策变量,均为整数变量)
A = -[ 1 2 0 0 0 0 1;
0 0 3 2 1 0 1;
4 1 0 2 4 6 1]; % 线性不等式约束的系数矩阵
b = -[100 100 100]'; % 线性不等式约束的常数项向量
lb = zeros(7,1); % 约束变量的范围下限
[x,fval]=intlinprog(c,intcon,A,b,[],[],lb)
最大最小化模型
例题
多目标规划模型
参考资料
【数学建模】多目标规划_SuperSources的博客-CSDN博客_多目标规划
数模3—Matlab线性规划、非线性规划、多目标规划(超全解法合集)_day by day get on的博客-CSDN博客_非线性规划matlab编程求最大值
下面例题来源:https://shenlong.blog.csdn.net/article/details/110501496
多目标遗传算法: https://zstar.blog.csdn.net/article/details/119302954
![]()
function f = mutiplesubjiect(x)
f(1)=3*x(1)-2*x(2);
f(2)=-4*x(1)-3*x(2);
% 单独对每个目标线性规划:
f1=[3;-2];
a=[2 3;2 1];
b=[18;10];
lb=[0;0];
ub=[];
[x,favl]=linprog(f1,a,b,[],[],lb,ub);
% 输出结果为:x=0.0000 6.0000,favl=-12.0000,所以最大值为12.0000
f2=[-4;-3];
[x,favl]=linprog(f2,a,b,[],[],lb,ub);
% 输出结果为:x=3.0000 4.0000,favl=-24.0000,所以最大值为24.0000
% 所以得到目标goal和权重
goal=[12,24];
weight=[12,24];
x0=[0;0];
[x,fval] = fgoalattain('mutiplesubjiect',goal,weight,x0,a,b,[],[],lb,[])