[MATLAB]数值计算
数值计算
- 一、数值微积分
-
- 1.1 数值积分integral
- 1.2 微分方程的求解
-
- 1.2.1 微分方程的解析解dsolve
- 二、数据分析
-
- 2.1 数据分析
- 2.2 reshape
- 三、矩阵和代数方程
-
- 3.1 矩阵的特征参数
- 3.2 矩阵的特征值与特征向量
- 3.3 矩阵的分解
-
- 3.3.1 三角形分解(LU分解)
- 3.3.2 正交分解(QR分解)
- 3.4 解线性方程组
-
- 3.4.1 线性方程组
- 3.4.2 几种解线性方程的函数
- 3.4.3 齐次线性方程组
- 3.4.4 非齐次线性方程组
- 四、多项式运算
-
- 4.1 多项式的表示
- 4.2 显示多项式
-
- 4.2.1 多项式的生成——系数法poly2sym
- 4.2.2 多项式的生成——根逆推法poly
- 4.3 多项式求值polyval
- 4.4 多项式的求根和求导
- 4.5 多项式的四则运算
-
- 4.5.1 多项式乘法运算函数conv(P1,P2)
- 4.5.2 多项式除法运算函数[div, rest] = deconv(a,b)
- 五、插值与拟合
-
- 5.1 多项式拟合polyfit(x,y,n)
- 5.2 拟合与插值的区别
- 5.3 拟合应用
一、数值微积分
1.1 数值积分integral
定积分指令:integral
q = integral (fun,xmin,xmax)
q = integral (fun,xmin,xmax,Name,Value)
- 输入量fun为被积函数的句柄
- 输入量xmin, xmax分别是积分的下限和上限,都必须是确定的数值;
- 输入量Name和Value是积分指令的选项,用于控制绝对误差等;
- 二重和三重积分使用integral2和integral3指令
>> f = @(x)exp(-x.*x);
>> integral(f, 0, 1)
ans =
0.7468
方法2:符号计算
>> syms x
>> f = exp(-x.*x);
>> int(f, x, 0, 1)
ans =
(pi^(1/2)*erf(1))/2
1.2 微分方程的求解
1.2.1 微分方程的解析解dsolve
dsolve(‘方程1’, ‘方程2’,…‘方程n’, ‘初始条件’, ‘自变量’)
在表达微分方程时,用字母D表示求微分,D2、D3等表示求高阶微分
![[MATLAB]数值计算_第2张图片](http://img.e-com-net.com/image/info8/85bf403f319e4e338d7660784a0a3c29.jpg)
![[MATLAB]数值计算_第3张图片](http://img.e-com-net.com/image/info8/cd1f01afe02d45d8985ea6856edf5acb.jpg)
>> dsolve('Du = 1 + u^2', 't')
ans =
tan(C5 + t)
1i
-1i
>> dsolve('D2y+4*Dy+29*y=0', 'y(0)=0,Dy(0)=15','x')
ans =
3*sin(5*x)*exp(-2*x)
二、数据分析
2.1 数据分析
- 如果输入是向量,则按整个向量进行分析
- 如果输入的是矩阵,则按列进行分析
数值分析函数
![[MATLAB]数值计算_第5张图片](http://img.e-com-net.com/image/info8/506c37bb1b0c415aa3b1390246a06bab.jpg)
median:将每列从大到小排序,之后计算中位数
![[MATLAB]数值计算_第6张图片](http://img.e-com-net.com/image/info8/061fcb80b8b24518a3b5731412bc1007.jpg)
如第二列从大到小排序后,计算(11+7)/2
A =
4 8 -9
11 -12 4
-8 0 5
6 5 10
>> sum(A,2) % 各行元素之和
ans =
3
3
-3
>> sort(A,2)
ans =
-9 4 8
-12 4 11
-8 0 5
2.2 reshape
A =
16 2 3 13
5 11 10 8
9 7 6 12
4 14 15 1
>> B = reshape(A ,4,4) % 将魔方阵重塑为4*4的矩阵
B =
16 2 3 13
5 11 10 8
9 7 6 12
4 14 15 1
>> B = reshape(1:16 ,4,4) % 将魔方阵重塑为4*4的矩阵
B =
1 5 9 13
2 6 10 14
3 7 11 15
4 8 12 16
三、矩阵和代数方程
3.1 矩阵的特征参数
3.2 矩阵的特征值与特征向量
[V,D]=eig(A),求解矩阵A的特征值D与特征向量V,AV=VD
>> A=[0 1;-1 0];
>> [V,D] = eig(A)
V =
0.7071 + 0.0000i 0.7071 + 0.0000i
0.0000 + 0.7071i 0.0000 - 0.7071i
D =
0.0000 + 1.0000i 0.0000 + 0.0000i
0.0000 + 0.0000i 0.0000 - 1.0000i
3.3 矩阵的分解
3.3.1 三角形分解(LU分解)
[L,U] = lu(A)
将方阵A表示成一个换位的下三角方阵L和一个上三角矩阵U的乘积
>> A=[5 2 0;2 6 2;5 6 7];
>> [L,U] = lu(A)
L =
1.0000 0 0
0.4000 1.0000 0
1.0000 0.7692 1.0000
U =
5.0000 2.0000 0
0 5.2000 2.0000
0 0 5.4615
3.3.2 正交分解(QR分解)
[Q,R] = qr(A)
将矩阵A表示成一个正交矩阵Q和一个上三角矩阵R的乘积
>> A=[1 2 3;4 5 6;7 8 9];
>> [Q,R] = qr(A)
Q =
-0.1231 0.9045 0.4082
-0.4924 0.3015 -0.8165
-0.8616 -0.3015 0.4082
R =
-8.1240 -9.6011 -11.0782
0 0.9045 1.8091
0 0 -0.0000
3.4 解线性方程组
3.4.1 线性方程组
线性方程组:未知量均为一次的方程组(n元一次方程组)
![[MATLAB]数值计算_第9张图片](http://img.e-com-net.com/image/info8/f2da3b4a88e54932b54c99ba921fd1d6.jpg)
矩阵形式:Ax = b
3.4.2 几种解线性方程的函数
3.4.3 齐次线性方程组
Ax = 0 称为齐次线性方程组
>> A=[1,-3,-1;1,-1,-19];
>> null(A)
ans =
0.9515
0.3058
0.0340
3.4.4 非齐次线性方程组
Ax = b 称为非齐次线性方程组
若秩(A) ≠ 秩(A,b),则无解;
若秩(A) = 秩(A,b) = n, 存在唯一解;
若秩(A) = 秩(A,b) < n, 存在无穷多解;
当方程有无穷多解时,通解是齐次线性方程组 Ax=0 的基础解系与 Ax=b 的一个特解之和。
左除法 A\B 求解矩阵方程AX=B
右除法 B/A 求解矩阵方程XA=B
若为唯一解, A\B将给出正确的解;
若方程组有无穷多解, A\B将给出一个特解,通解是齐次线性方程组 Ax=0 的基础解系null(A)与 A\B之和;
若方程组无解, A\B给出最小二乘意义上的近似解。
![[MATLAB]数值计算_第11张图片](http://img.e-com-net.com/image/info8/1b3366d13cdd4bd8be030c1e797bd280.jpg)
>> A = [1 2 ; 3 -2];
>> B = [1;4];
>> rank(A)
ans =
2
>> rank([A,B])
ans =
2
>> A\B
ans =
1.2500
-0.1250
>> A = [2 -2 3 ; -1 1 -2 ; 1 -1 1];
>> B = [5;3;8];
>> r1 = rank(A);
>> r2 = rank(B);
>> x0 = A \ B
警告: 矩阵为奇异工作精度。
x0 =
NaN
NaN
-11
% 由于不能直接解出,结果为非数,所以需要给原方程加上一个方程:0x1+0x2+0x3 = 0
>> a = [2 -2 3; -1 1 -2; 1 -1 1; 0 0 0];
>> b = [5;3;8;0];
>> x1 = a \ b;
>> x = null(a)
x =
-0.7071
-0.7071
0.0000
四、多项式运算
4.1 多项式的表示

例如:
2x3 - x2 + 3 <——> [2, -1, 0, 3] 系数中的0不能省
4.2 显示多项式
4.2.1 多项式的生成——系数法poly2sym
>> A = [1 2 3 4 5];
>> poly2sym(A)
ans =
x^4 + 2*x^3 + 3*x^2 + 4*x + 5
4.2.2 多项式的生成——根逆推法poly
% 已知根向量A = [1 -31 -80 0 0];
>> A = [1 -31 -80 0 0];
>> PA = poly(A);
>> poly2sym(PA)
ans =
x^5 + 110*x^4 + 2369*x^3 - 2480*x^2
4.3 多项式求值polyval
polyval(p, x) % 计算多项式p在x点的值
>> p = [2 -1 0 3];
>> x = 2;
>> y = polyval(p, x)
y =
15
>> x = [-1 2 : -2 1];
>> y = polyval(p, x)
y =
0 4
4.4 多项式的求根和求导
求多项式的根就是求解多项式f(x)=0的值。
roots(多项式向量)函数来求解出这个多项式的根。
>> P = [4 -3 2 -5];
>> x = roots(P)
x =
1.2007 + 0.0000i
-0.2253 + 0.9951i
-0.2253 - 0.9951i
>> x = [3 3.6];
>> polyval(P, x)
ans =
82.0000 149.9440
4.5 多项式的四则运算
4.5.1 多项式乘法运算函数conv(P1,P2)
>> a = [1 2 3];
>> b = [4 5 6];
>> c = conv(a, b)
c =
4 13 28 27 18
>> poly2str(c, 'x')
ans =
4 x^4 + 13 x^3 + 28 x^2 + 27 x + 18
4.5.2 多项式除法运算函数[div, rest] = deconv(a,b)
>> a = [1 2 3];
>> b = [4 5 6];
>> [div, rest] = deconv(a, b)
div =
0.2500
rest =
0 0.7500 1.5000
五、插值与拟合
5.1 多项式拟合polyfit(x,y,n)
多项式拟合:利用已知的离散数据估计未知点过程
- 求x,y数组所给数据的n阶拟合多项式系数向量p
- 多项式的阶数n要取得适当。
- 用一个多项式来逼近一组给定的数据
- 从几何上讲,并不要求曲线严格通过已知点,但要求曲线在各数据点和已知数据点之间的总体误差最小
5.2 拟合与插值的区别
- 曲线拟合研究如何寻找“平滑”曲线最好地表现带噪声的“测量数据”,但并不要求拟合曲线穿过这些“测量数据”点。
- 插值是在认定所给“基准数据”完全正确的情况下,研究如何“平滑”的估算出“基准数据”之间其他点的函数值,因此插值所得曲线一定穿过“基准数据”。
5.3 拟合应用
>> x = 1949 : 5 : 1994;
>> y=[541.67,602.66,672.09,704.99,806.71,908.59,975.42,1034.75,1106.76,1176.74];
>> p = polyfit(x,y,3)
p =
1.0e+07 *
-0.0000 0.0000 -0.0049 3.1995
>> x1 = 1995
x1 =
1995
>> y1 = polyval(p,x1);
>> y1 = polyval(p,x1)
y1 =
1.1821e+03
![[MATLAB]数值计算_第1张图片](http://img.e-com-net.com/image/info8/06269e6a66044e4f9df43fd49ae5d9d7.jpg)
![[MATLAB]数值计算_第4张图片](http://img.e-com-net.com/image/info8/c7621b72bd0841d9985a390cb5c8722c.jpg)
![[MATLAB]数值计算_第7张图片](http://img.e-com-net.com/image/info8/9e57888ed9b74b238545741c295c0aeb.jpg)
![[MATLAB]数值计算_第8张图片](http://img.e-com-net.com/image/info8/19b6fa4330bc45b9960373c8f462ed48.jpg)
![[MATLAB]数值计算_第10张图片](http://img.e-com-net.com/image/info8/4ca7bdf153b34aa4a4e02b0096d37f35.jpg)
![[MATLAB]数值计算_第12张图片](http://img.e-com-net.com/image/info8/5a7b806658284b508ef9dd8fc43407fc.jpg)


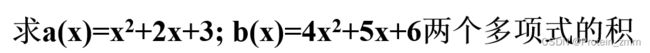
![[MATLAB]数值计算_第13张图片](http://img.e-com-net.com/image/info8/94aff35f4a3d420b9b9bc0b142578ff7.jpg)