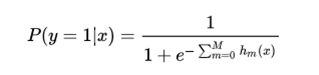机器学习|GBDT
GBDT (Gradient Boosting Decision Tree)梯度提升迭代决策树也是boosting算法的一种,但是和adaboost算法不同,区别如下:adaboost算法是利用前一轮的弱学习器的误差来更新样本权重值;GBDT做分类还是回归要求弱学习器是cart回归树,每个弱学习器在上一轮学习器的残差基础上进行训练。
目录
预热
GBDT做回归算法原理
GBDT做分类算法原理
代码展示
总结
一、GBDT预热
回顾:cart回归树的分裂条件是MSE/MAE
为什么GBDT做分类和回归的弱学习器都是回归树?
gbdt的原理是boosting的思想,且其最终的结果是把每棵小树的结果进行加和,所以每棵小树的结果必须是回归出来的数值,加起来才有意义。如果是分类树,所得结果是概率,对每棵小树结果(概率)加和无意义。
所以说 GBDT的基树的分裂条件是MSE 与GBDT的损失函数(GBDT做回归:MSE ;GBDT做分类:交叉熵)无关
二、GBDT做回归算法原理
算法原理:
1、基模型是回归树,每棵回归树f(x)的分裂条件及损失为 1/2 Σ(y-f(x))²
2、GBDT引用梯度下降的思想 Wt = W(t-1) - a·g(t-1)
则函数空间的梯度下降变为Ft(x) = Ft-1(x) - a ·g(t-1)
-gt就为上一棵树对函数的偏导得 yi - f(xi) 及残差:
3.所以使用下一棵树去拟合上一棵树的残差
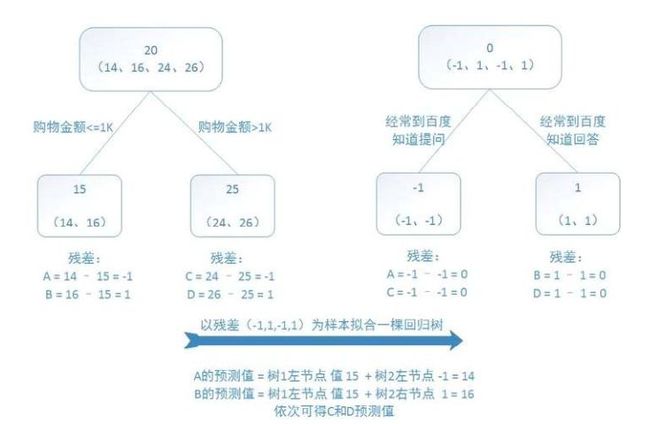
举例说明:
1.样本数据14,16,24,26(4条) ,均值为20
2.计算mse增益最大,找到两个分裂条件(购物金额<=1K,购物金额>1K),并进行分裂
3.左子节点为14,16两条样本且均值为15,右子节点为24,26两条样本且均值为25
4.所以样本A的残差为:y - y_hat = 14 - 15(叶子节点均值) = -1
同理样本B的残差为1 ;C样本 残差为-1 ;D样本残差1
5.用第二棵小树去拟合第一棵小树的残差,则样本变为(-1,1,-1,1)
6.同样进行第2步的迭代,找到两个分裂条件(经常到百度提问,经常到百度回答),并进行分裂
7.同理计算第二棵树各个样本残差 A = -1 - -1 =0 ,B = 0 ,C = 0,D = 0
模型F(X) =f1(x) + f2(x) 则A,B,C,D样本预测值分别为14,14,26,26
三、GBDT做分类算法原理
通过一个简单的二分类问题,来研究GBDT是如何学习到一棵树的。
类似于逻辑回归分类问题,其实是用一个线性模型去拟合对数几率 ln[ p/(1-p) ] 。而GBDT也是一样,用一系列的梯度提升树去拟合这个对数几率,实际上最终得到的是一些了cart回归树。其分类模型可以表达为:
其中hm(x)就是学习到的基模型回归树
逻辑回归的损失函数可以表达为交叉熵:
GBDT的表达式为F(x) =Σhm(x) ,将yi_hat 的表达式代入之后:
可以看到,同回归问题一样,分类问题下一棵基cart回归树同样需要拟合残差(真实标签与预测概率之差)进行迭代
四、GBDT代码展示
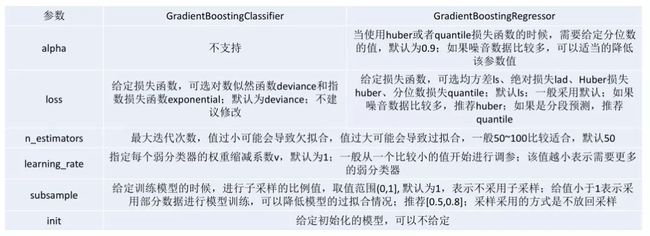
sklearn相关参数
code:
# -*- encoding: utf-8 -*-
from sklearn.datasets import load_digits
from sklearn.metrics import classification_report
from sklearn.model_selection import train_test_split
from sklearn.ensemble import GradientBoostingClassifier
from matplotlib import pyplot as plt
import numpy as np
# 1.加载数据 手写字体数据集
digits = load_digits()
X = digits.data
y = digits.target
# 数据切分
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.33, random_state=42)
# 2.构建模型
dtc = GradientBoostingClassifier(loss='deviance', learning_rate=0.005, n_estimators=100, subsample=1.0,
min_samples_split=2, min_samples_leaf=1, min_weight_fraction_leaf=0., max_depth=3,
init=None, random_state=None, max_features=None, verbose=0, max_leaf_nodes=None,
warm_start=False, presort='auto')
# 3.训练模型
dtc.fit(X_train, y_train)
# 3.测试
y_pred = dtc.predict(X_test)
n_samples, n_features = X_test.shape
'''显示原始数据'''
n = 20 # 每行20个数字,每列20个数字
img = np.zeros((10 * n, 10 * n))
for i in range(n):
ix = 10 * i + 1
for j in range(n):
iy = 10 * j + 1
img[ix:ix + 8, iy:iy + 8] = X_test[i * n + j].reshape((8, 8))
plt.figure(figsize=(8, 8))
plt.imshow(img, cmap=plt.cm.binary)
plt.xticks([])
plt.yticks([])
plt.show()
# 4.模型校验
print(f"Model in train score is:", dtc.score(X_train, y_train))
print("Model in test score is:", dtc.score(X_test, y_test))
print("report is:", classification_report(y_test, y_pred))Model in train score is: 0.9301745635910225
X_test数据集合:
Model in train score is: 0.9301745635910225
Model in test score is: 0.8754208754208754
report is: precision recall f1-score support
0 0.98 0.91 0.94 55
1 0.89 0.87 0.88 55
2 0.91 0.79 0.85 52
3 0.89 0.88 0.88 56
4 0.92 0.91 0.91 64
5 0.97 0.81 0.88 73
6 0.87 0.95 0.91 57
7 0.80 0.92 0.86 62
8 0.79 0.92 0.85 52
9 0.79 0.82 0.81 68
accuracy 0.88 594
macro avg 0.88 0.88 0.88 594
weighted avg 0.88 0.88 0.88 594
五、GBDT总结
GBDT的主要优点:
(1)可以灵活处理各种类型的数据,包括连续值和离散值。
(2)在相对少的调参时间情况下,预测的准确率也可以比较高。
(3)模型的鲁棒性比较强
GBDT的主要缺点:
(1)由于弱学习器之间存在依赖关系,难以并行训练数据。
往期精选
机器学习|决策树
机器学习|随机森林
机器学习|Adaboost
数据分析|数据的整理&展示
数据分析|数据分布特征的描述
数据分析|概率分布
数据分析|抽样分布
数据分析|参数估计
关注公众号,加小编微信即可拉入线上交流群