多元线性回归多重共线性的危害

多元线性回归多重共线性的危害

作者：居居
日期：2021-11-05

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif'] = ['SimHei'] # 步骤一（替换sans-serif字体）
plt.rcParams['axes.unicode_minus'] = False   # 步骤二（解决坐标轴负数的负号显示问题）

#载入数据：
data=pd.read_clipboard()
data.columns=["日期","需求量","本品价格","竞品价格","平均收入水平","广告投入"]

这是一份真实的数据，来自美国某高校商学院的示例数据库。阿三国（印度）某地方企业的芥末油（调味品）产品的需求量和其他影响因素的统计数据见下表。

研究目标是，根据统计数据，研究本品的"需求量"和其他的四个变量究竟有没有关系，注意：时间维度并不影响需求量

data.head(10)

	日期	需求量	本品价格	竞品价格	平均收入水平	广告投入
0	Apr-11	12890	65.00	69.22	4343.17	1170.00
1	May-11	12850	65.90	70.67	4347.59	1162.26
2	Jun-11	13180	65.40	74.77	4356.44	1164.06
3	Jul-11	13785	65.34	75.00	4369.71	1193.13
4	Aug-11	13880	66.00	75.00	4387.40	1241.55
5	Sep-11	12680	69.00	77.29	4409.51	1254.15
6	Oct-11	13290	69.00	79.06	4436.05	1149.57
7	Nov-11	13498	69.25	81.37	4467.01	1200.06
8	Dec-11	11980	74.56	84.00	4502.40	1220.40
9	Jan-12	12085	78.00	91.61	4542.20	1082.70

通常，我们会先画出因变量与其他四个自变量的关系，也就是绘制散点图。

从下面四张图中我们可以看出，4个自变量和因变量之间似乎存在线性关系。

fig,ax=plt.subplots(1,4,figsize=(18,4),dpi=150)
for i,xName in zip(np.arange(0,4,1),data.columns[2:]):
    ax[i].scatter(data.loc[:,"需求量"],data.loc[:,xName])
    ax[i].set_xlabel("需求量")
    ax[i].set_ylabel(xName)

然后我们进行多元线性回归

import statsmodels.api as sm
X=data.loc[:,["本品价格","竞品价格","平均收入水平","广告投入"]]#解释变量
X["const"]=1#添加常数项
Y=data['需求量']#被解释变量
model = sm.OLS(Y, X).fit()#模型拟合
model.summary2()#统计信息汇总

Model:	OLS	Adj. R-squared:	0.670
Dependent Variable:	需求量	AIC:	869.0905
Date:	2021-11-05 11:53	BIC:	879.0355
No. Observations:	54	Log-Likelihood:	-429.55
Df Model:	4	F-statistic:	27.96
Df Residuals:	49	Prob (F-statistic):	4.07e-12
R-squared:	0.695	Scale:	5.2354e+05

	Coef.	Std.Err.	t	P>|t|	[0.025	0.975]
本品价格	-136.6168	44.8461	-3.0463	0.0037	-226.7384	-46.4952
竞品价格	117.4078	39.3116	2.9866	0.0044	38.4081	196.4074
平均收入水平	-0.2823	0.1511	-1.8688	0.0676	-0.5860	0.0213
广告投入	7.8651	1.0474	7.5093	0.0000	5.7603	9.9699
const	5024.5753	1945.0948	2.5832	0.0128	1115.7609	8933.3897

Omnibus:	1.001	Durbin-Watson:	1.434
Prob(Omnibus):	0.606	Jarque-Bera (JB):	0.556
Skew:	-0.241	Prob(JB):	0.757
Kurtosis:	3.123	Condition No.:	115795

以上结果在我们通常看来是非常漂亮的，调整后的R2=0.67，F检验和T检验都在0.05水平显著。

然后结论就是：

在其他变量都保持不变的情况下，需求量

1.跟本品价格成负相关

2.跟竞品价格成正相关

3.跟收入水平成负相关

4.跟广告投入成正相关

这些结论貌似很合理？！

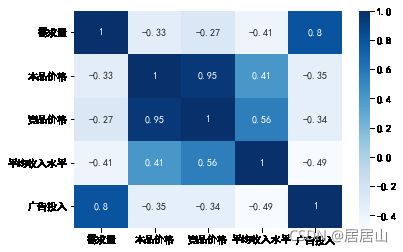
我们来做一个相关系数矩阵看看，竞品价格和本品价格存在共线性，相关系数大于0.7，为0.95，几乎就是完全相关。

import seaborn as sns
sns.heatmap(data.corr(), cmap='Blues', annot=True)

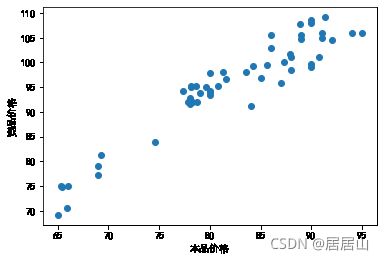
绘制本品价格和竞品价格的散点图，可以看出本品和竞品真的相关性极强，回归方程的R2高达0.896。

plt.scatter(data["本品价格"],data["竞品价格"])
plt.xlabel("本品价格")
plt.ylabel("竞品价格")
plt.show()
X=data.loc[:,["竞品价格"]]#解释变量
X["const"]=1#添加常数项#添加常数项
Y=data['本品价格']#被解释变量
model = sm.OLS(Y, X).fit()#模型拟合
model.summary2()#统计信息汇总

Model:	OLS	Adj. R-squared:	0.896
Dependent Variable:	本品价格	AIC:	258.5114
Date:	2021-11-05 11:53	BIC:	262.4893
No. Observations:	54	Log-Likelihood:	-127.26
Df Model:	1	F-statistic:	459.1
Df Residuals:	52	Prob (F-statistic):	1.82e-27
R-squared:	0.898	Scale:	6.7736

	Coef.	Std.Err.	t	P>|t|	[0.025	0.975]
竞品价格	0.7649	0.0357	21.4255	0.0000	0.6933	0.8366
const	9.0352	3.4150	2.6458	0.0108	2.1826	15.8878

Omnibus:	4.083	Durbin-Watson:	0.724
Prob(Omnibus):	0.130	Jarque-Bera (JB):	3.626
Skew:	0.550	Prob(JB):	0.163
Kurtosis:	2.366	Condition No.:	922

fig,ax=plt.subplots(figsize=(15,3),dpi=150)
plt.plot(data.loc[:,"日期"],data.loc[:,"竞品价格"]-data.loc[:,"本品价格"])
plt.xlabel("日期")
plt.ylabel("竞品-本品价格差")
for tick in ax.get_xticklabels():

        tick.set_rotation(90)

竞品在任何时间点上的价格都高于本品，说明价格上竞品没有优势。

所以我们完全可以忽略竞品价格的影响，消除多重共线性，剔除竞品价格再次进行回归得到以下结果：

X=data.loc[:,["本品价格","平均收入水平","广告投入"]]#解释变量
X["const"]=1#添加常数项#添加常数项
Y=data['需求量']#被解释变量
model = sm.OLS(Y, X).fit()#模型拟合
model.summary2()#统计信息汇总

Model:	OLS	Adj. R-squared:	0.618
Dependent Variable:	需求量	AIC:	876.1214
Date:	2021-11-05 11:53	BIC:	884.0773
No. Observations:	54	Log-Likelihood:	-434.06
Df Model:	3	F-statistic:	29.61
Df Residuals:	50	Prob (F-statistic):	3.78e-11
R-squared:	0.640	Scale:	6.0647e+05

	Coef.	Std.Err.	t	P>|t|	[0.025	0.975]
本品价格	-9.1044	14.7697	-0.6164	0.5404	-38.7702	20.5614
平均收入水平	-0.0074	0.1289	-0.0573	0.9546	-0.2664	0.2516
广告投入	8.5976	1.0959	7.8450	0.0000	6.3963	10.7989
const	3420.3152	2012.0704	1.6999	0.0954	-621.0471	7461.6774

Omnibus:	0.946	Durbin-Watson:	1.749
Prob(Omnibus):	0.623	Jarque-Bera (JB):	0.336
Skew:	-0.093	Prob(JB):	0.846
Kurtosis:	3.338	Condition No.:	111271

突然本品价格和平均收入水平两个变量也不显著了，那么。。。。这个结果就很难看了。甚至此时，很多人可能会认为不能踢掉竞品价格，因为它会让模型的表现变差，但是。。。事实果真如此吗？

然后我们做出4个自变量和因变量的时序图

我们从最简单的分析开始：

1.图1可以看出，需求量一直在波动，而图4的人均收入一直在增长，讲真，关系不大。

2.图2和图3似乎也跟图1的相关性不明显，结合相关关系矩阵可以知道，他们线性相关性极弱。即便是在本品价格很高的时候，需求量也可以很大啊。。。

3.图5和图1的趋势几乎相同。

说明：

就数据而言，需求量真的就只和广告投入有关

fig,ax=plt.subplots(5,1,figsize=(15,28),dpi=100)

for i,xName in zip(np.arange(0,5,1),data.columns[1:]):
    ax[i].plot(data.loc[:,"日期"],data.loc[:,xName],)
    ax[i].set_xlabel("日期")
    ax[i].set_ylabel(xName)
    
    
    for tick in ax[i].get_xticklabels():

        tick.set_rotation(90)

于是乎，我们得到了正确的方程：

其实这个芥末油的推广模式就是。。。在小卖部贴小广告，每个月的花费只有1000多印度卢比，差不多只有100元人民币。

通过方程，我们可以很容易计算出，每多花10卢比贴海报，就可以多销售125瓶，是不是很划算？

X=data.loc[:,["广告投入"]]#解释变量
X["const"]=1#添加常数项#添加常数项
Y=data['需求量']#被解释变量
model = sm.OLS(Y, X).fit()#模型拟合
model.summary2()#统计信息汇总

Model:	OLS	Adj. R-squared:	0.630
Dependent Variable:	需求量	AIC:	872.5980
Date:	2021-11-05 11:53	BIC:	876.5760
No. Observations:	54	Log-Likelihood:	-434.30
Df Model:	1	F-statistic:	91.12
Df Residuals:	52	Prob (F-statistic):	5.05e-13
R-squared:	0.637	Scale:	5.8831e+05

	Coef.	Std.Err.	t	P>|t|	[0.025	0.975]
广告投入	8.8527	0.9274	9.5458	0.0000	6.9917	10.7136
const	2361.8148	993.4918	2.3773	0.0212	368.2277	4355.4019

Omnibus:	1.747	Durbin-Watson:	1.800
Prob(Omnibus):	0.417	Jarque-Bera (JB):	0.960
Skew:	-0.239	Prob(JB):	0.619
Kurtosis:	3.445	Condition No.:	10197

百度百科词条中，多重共线性存在的影响主要有：

（1）完全共线性下参数估计量不存在

（2）近似共线性下OLS估计量非有效

（3）参数估计量经济含义不合理

（4）变量的显著性检验失去意义，可能将重要的解释变量排除在模型之外

（5）模型的预测功能失效。变大的方差容易使区间预测的“区间”变大，使预测失去意义。

所以，第一个模型中，由于本品价格和竞品价格高度相关，所以得出的结果对我们产生了误导。

因此，正确使用统计学方法才能得到准确的结果，及时它是违背直觉的。你说。。。是吧？

多说两句，正确的结果可能会让你发不出论文（手动狗头），但是能给你企业省一大笔钱。就像上面的例子中，

现阶段我只要增加广告投入即可。 但是如果你只是关注模型的预测能力，似乎。。。你不关注共线性也行。。。

本文还有一些坑，需要填，因为时间关系，我并没有考察偏相关性。这个请大家自行验证。

然后，根据我老师的建议，如果大家想深入学习，可以阅读《统计反思》第五章关于多重共线的相关章节。

我不是经济学人，所以对竞品市场之类的概念不太懂，就数据论结果，欢迎交流，不喜勿喷。