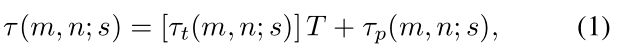【论文笔记】Ultra Reliable, Low Latency V2I Wireless Communications with Edge Computing
超可靠低延迟的V2I通信是无人驾驶汽车（AV）的关键要求。 为此，具有边缘计算功能的蜂窝小型基站（SBS）可以通过本地处理来自AV的任务请求来减少端到端（E2E）服务延迟，无需将任务转发到远程云服务器。 但是，由于SBS的计算能力有限，再加上无线带宽资源的稀缺性，最大程度地减小AV的E2E延迟并实现可靠的V2I网络是一项挑战。本文提出了一种新算法来联合优化AV与SBS的连接和带宽分配，以最大化V2I网络的可靠性。 他参考了劳动力匹配市场的算法，可以有效地执行AV与SBS的分布式关联，同时考虑AV的延迟需求以及SBS的有限计算和带宽资源。
介绍
与AV相关的大多数任务是需要低延迟的可靠处理。因此，V2I无线系统必须能够在严格的延迟和可靠性要求下管理AV的请求任务[5] – [7]。
蜂窝V2I通信与边缘计算集成的难点： 首先，小型小区BS（SBS）的计算资源有限，因此AV任务很容易使它们过载。 第二，在V2I系统中用于AV任务管理的端到端（E2E）延迟取决于：a）上行链路传输延迟（即，向SBS请求任务）；b）边缘机的计算延迟；c）将处理后的任务发送给AV的下行传输延迟。一旦与异构任务和无线信道的随机变化结合在一起，在V2I网络中优化E2E服务质量（QoS）就变得非常具有挑战性，并且需要高效的AV-SBS协同以及无线和计算资源管理。
最近已出现一些解决上述V2I挑战的工作[5]，[11]-[14]。 在[5]中，作者研究了传输时间间隔（TTI）对低延迟车辆通信性能的影响。 [12]调查了V2I网络中各种软件定义的延迟控制方案。 [13]开发了一种边缘计算框架来减少车辆服务的计算等待时间。[14]提出了用于实现低延迟车辆通信的另一种无线资源管理方法。 同时，大多数有关AV-SBS协同的工作（例如，参见[15]及其参考文献）的优化目标均为常规指标，例如最大信号干扰加噪声比（max-SINR）和最大接收信号强度指示符（max-RSSI ）。
但是，[5]，[11]-[14]中的都是孤立地研究计算和通信延迟的，而不是从端到端的角度。 例如，[5]中的工作考虑了计算延迟的固定值，而忽略了端到端延迟。 另外，[14]中的作者只关注无线资源管理，而没有考虑计算延迟。 此外，现有的工作大多依赖于集中式资源管理，而需要快速而有效的分布式算法来管理密集V2I网络中的任务。
资源管理的集中式和分布式的区别在于：前者的无线资源管理功能集中在一个高层网元中，后者将无线资源管理功能下放到底层的基站中，这样就节省了基站和高层网元信令交互传输的时间。
本文提出一个低延时的V2I通信框架，它可以通过联合优化AV-SBS的无线资源管理来提高可靠性。为此，我们基于匹配理论构建了一种新颖的解决方案，该解决方案可以解决AV任务的端到端时延要求以及SBS的有限计算和带宽资源带来的问题。 为了解决此问题，我们提出了一种新颖的算法，该算法将AV与SBS迭代关联，并分配带宽。 实践证明，该算法能够收敛于AV与SBS之间的核心分配，从而保证了V2I网络在使用分布式实现时的稳定性。 仿真结果表明，与max-SINR和maxRSSI作优化目标相比，该算法可最大程度地提高V2I系统的可靠性和最小化AV的E2E延迟。
系统模型
考虑面积为A的正方形区域的无线蜂窝网，由N个均匀分布的SBS组成，其整体记作
。在该网络中，M个AV组成的集合
被随机部署，并且必须与SBS通信。 自然，AV的无缝运行需要实时管理多个任务。 表I总结了典型任务及其延迟要求的列表。 为了避免回程网络的延迟，SBS配备了边缘计算机，以处理来自AV的任务集合
中的任务(比如单个AV无法完成的高清地图构建)，并将必要的信息发送到AV。
考虑到SBS的边缘计算能力，可以将AV m∈ 和SBS n∈ 之间的V2I通信的E2E传输时延定义为
其中T 是一个TTI的持续时间（以毫秒为单位），
（m，n; s）是任务s的传输时延。 另外，
（m，n； s）是在SBS n的边缘单元处理AV m的任务s的计算时延。 接下来，我们详细描述传输和处理延迟。
整体的传输时延是上行和下行传输延迟的和：
其中
表示下行传输时延，是AV m 将任务 s 发送到SBS n 所用的时延，由下计算：？？
-
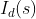表示下行传输的任务 s 的包的尺寸/bit -
分母表示一个TTI内传输的下行链路数据。为了有效利用时频资源，我们考虑了带宽为W的正交频分复用（OFDM）帧结构，他被均匀地分成K个子信道，用集合
表示，每个子信道都有带宽 
。 因此，下行速率为：
其中
= 1，表示子信道k被SBS n分配到 AV m，否则为0；可知下行链路的SINR：
会影响下行速率：
其中
分别表示：SBS n的传输功率，SBS n‘对AV m的干扰，噪声功率。在(5)中，
和
分别表示AV m和SBS n的天线增益。 
和
分别表示子信道k处的瑞利衰落信道增益和AV m与SBS n之间的下行链路路径损耗。 在低延迟V2I中TTI持续时间很小（约为一个OFDM符号持续时间[5]），因此，信道增益（和（4）中的速率）可以认为在一个数据包的传输过程中是恒定的 。
类似于（3），我们可以得到上行传输时延
，上行链路的SINR由下式给出：
其中
是AV m的发射功率，
是在子信道k’中传输的来自另一个AV m’的干扰。假设V2I中的上行链路流量主要是较小的数据包（例如，请求服务或发送短控制数据包），我们假设上行链路传输通过子信道k‘
管理。??
SBS的计算时延是一个随机变量。 这种随机性主要源于：任务的执行时间取决于要处理的数据[10]。此外SBS计算机的类型一致与否也会影响计算时延，类型不一致的SBS对同一个任务的计算时延将不同。由于这种不确定性，通常定义一个概率质量函数（pmf），用于表示由边缘机SBS 
通过
个时间步长 [10]来完成的任意任务
的计算时延。
在不失一般性的前提下，我们考虑每个SBS使用一台边缘计算机。 在V2I方案中，可以将多个任务分配给SBS。 在这种情况下，分配给（SBS的）机器的任务在队列 µ(n) ⊆ 
中进行批处理。在这里，我们注意到任意任务 的完成时间pmf取决于队列µ(n)中的其他任务。 现在，通过对队列µ(n)中位于s之前的任务的执行时间pmf进行卷积，可以得到任务s∈μ(n)完成时间的pmf:
圈星表示卷积，
是在机器 中排队的任务的集合。通过上式，可以得到SBS中任务的预期完成时间：
其中
是 任务s进行之前的最大处理时间步数。
问题表述
考虑所提出的框架，目标是最大化V2I系统的可靠性，同时考虑每个AV任务的延迟要求。 考虑到这一点，我们定义伯努利随机变量 ，如下式：
其中
是任务s的可容忍E2E延迟，即如果任务s在小于其E2E延迟约束的时间内成功管理则(m,n; s)= 1，否则，(m，n; s) = 0。基于（9）和3GPP的可靠性定义[16]，我们可以将V2I系统可靠性定义为【此式的两个积项都是0/1】
对于![w_n = [w_{1n},w_{2n},..., w_{Mn}]](http://img.e-com-net.com/image/info8/10107aa5222b44f9bb9a2982ce98cae7.gif){kind=small}
，其中每个成员是 为
的带宽分配 
。 同时，如果AV m与SBS n相关，则
= 1，否则 =0。实际上，从(10)可见，网络可靠性取决于：1）AV与SBS的关联性； 2）每个SBS的带宽分配。 计算时延依赖于与SBS相关的AV的子集，如（7）所示。 因此，为了最大化可靠性η，面临的挑战是共同找到最佳的AV-SBS关联和资源分配，同时考虑到一个AV的传输和计算延迟受其他AV影响的事实。
AV m∈
到这里我们可以表述 AV-SBS协同和资源分配问题如下：
约束(12)和(13)表示每个AV最多与一个SBS相连、每个SBS最多与M个AV相连
(14)表示每个SBS的下行传输可以使用K个子信道
(15)确保每个小区内的子信道正交
最大化可靠性问题是一个NP-hard问题，其很难解决。下面我们提出通过以下架构解决这个问题
对低延迟V2I通信的匹配策略
为了在(11)-(16)的约束下共同优化AV-SBS关联策略和带宽分配，必须找到一种快速收敛的算法。 为此，我们基于匹配理论构建解决方案，尤其是，通过使用劳力市场中工人到公司的分配问题来模拟从AV到SBS的关联问题[18]。也就是说，考虑到一组工人（AVs）和一组公司（SBS），每个工人的目标是以尽可能高的薪水聘用，而公司的目的是雇用一部分使他们的收入最大化的工人。 接下来，使用这个双向框架，我们展示如何将V2I资源管理问题表达为劳动力匹配市场。
【A. SBS和AV的效用函数】
这里的效用函数，英文为Utility Function，文章将其视为目标函数来使用
为确保网络的低延时通信，每个SBS n可以以选择一组AV和对应的带宽分配策略，目标是最大化下面的效用函数
传输延迟在(2)式中给出，AV组 
的任务的计算时延是随机和未知。在式(17)中，SBS根据式(8)估计AV组的计算时延。式(17)的第一项与AV的带宽 
成反比，
是一个控制系数。分配的带宽可以视作服务AV的cost，因此，(17)的第一项将防止带宽分配的不公平。类比劳动力匹配市场，(17)中的第一项中的是公司支付给工人的工资。
这里的
每个AV m旨在与SBS相关联，并使端到端的延迟最小。但AV不知道其各自的任务在SBS的计算延迟。这是因为任务的计算延迟也和其他与该SBS相连的AV有关，如(7)所示。该信息由SBS提供。因此 AV 
的效用是：
由资源分配向量
决定。
【B.将V2I通信视作匹配问题】
使用为AV和SBS的效用函数，我们将提出的匹配问题定义如下：
定义 1. 一个AV-SBS的匹配映射 f ：
- 对任意AV m，
。
表示AV m未分配到任何SBS
- 对任意SBS n，
# 这里的
，iif
此定义还要确保满足(12)(13)的可行性约束
此外，服从带宽分配矢量![[\omega_1,\omega_2,...,\omega_N]](http://img.e-com-net.com/image/info8/01d662683ec94a949716f9417748cc27.gif){kind=small}
的映射可表示为![(f;[\omega_1,\omega_2,...,\omega_N])](http://img.e-com-net.com/image/info8/d3e1addb5b5a45479b19f215bf367165.gif){kind=small}
， 如果满足以下条件，则称为 个体合理分配(individually rational)：1）对于任何分配给SBS f(m)的AV，
> 0 # 表示AV m 和SBS f(m)之间的信道不为0； 2）对于任何SBS n，0 <
<∞ # SBS的效用必须是非负且有限的。 我们的目标是在个体合理的基础上找到AV到SBS的严格最佳(core)搭配，如下所述。
定义 2.一个个体合理分配的AV-SBS对（f ; w）是一个最佳搭配，如果不存在AV-SBS M'的配对（n, M'）(对应带宽分配矢量
)能做到：
，for all m
M‘
若存在满足以上两个条件的(n, M')，则可以通过阻断(blocking)映射f来改进他们的效用，并充分形成一个分配方案。本来，最佳搭配的概念就是通过阻止不理想的SBS-AV分配来保证V2I系统的稳定性。
但是找到最佳的AV到SBS的搭配具有很困难，因为AV和SBS的相互依赖的效用是基于以下两个事实：1）从(7)中，分配到同一SBS的AV的处理延迟相互关联 ; （2）根据(14)，对一个AV分配的带宽取决于对同一小区内的其他AV的资源分配。实际上，诸如延迟接受算法[19]之类的经典方法无法为V2I问题[18]产生核心分配。 因此，我们接下来提出一种新算法，该算法可确保找到AV对SBS的核心分配。
联合AV-SBS分配和资源管理的匹配算法
这里先按照人力市场的背景下解释一下此算法：
- step1：第一轮中，每个公司为每个求职者安排一个工资，然后求职者比较以下收到的offer，可以选择拒绝某个offer
- 当有求职者拒绝offer时，进入step2
- step2：每一轮中公司都要重新为求职者（但这里不一定是给每个人都要安排）安排一个工资，公司计算根据他发出去的offer算一算得到哪些人可让公司效益最大化，列出人员清单
- step3：综合考虑
- step4：每个人接收本轮中他受到的最好的offer，并拒绝其他offer
保证最佳搭配的关键思想是允许在执行AV-SBS关联时调整AV和SBS之间的带宽。 也就是说，SBS可为每个AV提供一个确定的端到端延迟（通过分配多个子信道），而AV可以接受报价或拒绝报价以与另一个SBS更好地分配。基于此思想，我们在表II中提出了一种新颖的算法，该算法如下进行：最初在回合j = 0，每个SBS为每个AV分配一个子信道。 随着算法的进行，每个SBS n在第j轮更新更新带宽分配向量![w_n(j)= [w_{1n}(j), w_{2n}(j), ... , w_{Mn}(j)]](http://img.e-com-net.com/image/info8/be5f44c63c7649188a7af00d27947baf.gif){kind=small}
。 更新规则：如果AV在第j-1轮中拒绝了SBS n的报价，则
； 否则，
。
在任一轮 j上，根据带宽分配
，每个SBS n∈N选择一个AV子集，以最大化其效用（17）。 在步骤2中执行AV选择过程。随后在步骤3中，综合考虑所有AV并根据自己的效用函数来选择一些AV，这些AV列入SBS的关联列表中，如果本轮的信道分配没有被AV拒绝，则在下一轮重复这个分配数值。 在步骤4中，每个AV暂时接受在（18）中最大化其效用的报价，并拒绝其余的报价。 最后，在步骤5中，SBS根据先前解释的规则来更新其带宽分配矢量，∀n∈N。 一旦AV没有拒绝报价，该算法就会收敛。 在证明所提出的算法收敛于最佳搭配之前，我们进行了以下初步观察：
备注1.每个AV在每一轮中至少有一个关联报价。
步骤1中，每个SBS将关联提议发送到所有AV。 由于在任何回合中，每个AV暂时都接受一个报价，在下一回合为此AV分配的带宽保持不变。 此外，从第3步开始，任何未被拒绝的报价都必须在下一轮中重复。 因此，在任何回合中，AV至少具有一个关联报价。
引理1. 经历有限的回合之后，每个AV都将有一个唯一的报价，算法收敛。
证明： 由备注1，我们注意到每个AV在每个回合中至少都有一个报价。 此外，根据步骤5中的带宽分配规则，下一轮SBS为AV分配的带宽必比上一轮大，除了接受其offer的AV。 同时，根据（17），SBS的效用是分配带宽的递减函数。 因此，随着算法的进行，每个AV收到的offer数量减少，直到每个AV仅接收到它接受的一个offer（带宽分配）。 由于此时没有拒绝发生，因此该算法收敛。
引理2. 表II中提出的算法收敛的最终结果为，AV和SBS的个体合理分配。
证明： 令![(f^*,[w^*_1,w^*_2,...,w^*_N])](http://img.e-com-net.com/image/info8/58e0ee0db2a64e63a33ab821dd1aa86b.gif){kind=small}
为经历j*次迭代所到达的收敛点的结果，因为在步骤1中，每个AV至少被分配到一个信道，在步骤5中，每一轮的带宽分配都要下降，因此对于所有m∈，
。从步骤2的AV选择过程中，由任意SBS n选择的AV子集将产生有限的正效用
。 因此，经过j ∗次迭代，
将为正，由此得证。
定理1. 表II中提出的算法保证收敛的结果中 AV和SBS的最佳搭配。
证明： 引理1显示了任意j *次迭代后所提出算法的收敛性。 令算法的结果为![(f,[w_1(j ^*),w_2(j ^*),...,w_N(j^*)])](http://img.e-com-net.com/image/info8/b4db4c517e30441a8c0725d829ef1920.gif){kind=small}
。我们通过反证法证明此结果是最佳搭配。假设此结果不是严格的核心分配。由于引理2中的是有理数，所以必须有一个SBS和a的阻塞对。 具有带宽分配矢量ˆ wn的AV子集（n，M 0），使得∀m∈M 0：
根据（19），在该算法的任何回合中，任何AV m∈M 0都绝不能从SBS n接收到带宽分配为ˆ w mn（或大于ˆ w mn）的提议。 否则，AV m将接受该报价。 同时，由于在每一轮之后分配给每个AV的带宽增加或保持恒定（根据步骤5中的更新规则），所以为了使SBS n与M 0中的AV形成阻塞对，带宽分配必须满足ˆ w 对于所有m∈M 0，mn≥w mf（m）。但是，鉴于SBS的效用是分配带宽的递减函数，则
其中（21）中的严格不等式直接由（20）引起。 实际上，（21）暗示SBS n将向M 0中的AV子集提出带宽分配矢量w n（j ∗），这与算法收敛的初始假设相矛盾。 因此，不存在这样的阻塞对，从而确保了对核心分配的收敛。
性能评估
【A. 仿真参数】
我们考虑一个面积为100 m×100 m的区域，其中AV和SBS随机分布在该区域中。 我们考虑10个SBS，而AV的数量从10到40不等。统计结果是大量独立运行的平均值。表III总结了仿真参数。
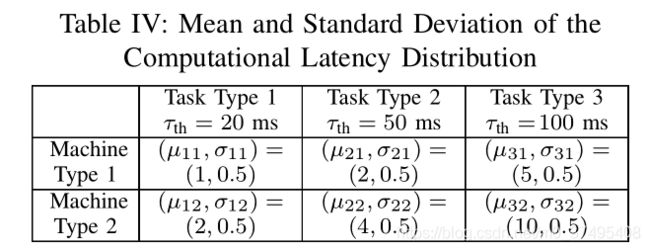
此外，我们从集合S = {s 1，s 2，s 3}中的三种任务类型为每个AV分配一个随机任务。 根据SBS的边缘计算能力，我们考虑两种具有不同等待时间分布的SBS来管理S中的任务。对于在机器类型j∈{1,2}上处理的每个任务si∈S，其pmf 计算等待时间遵循高斯分布N（μij，σ2 ij），均值μij和方差σ2 ij [10]，如表IV所示。 表IV中还指定了每种任务类型可容忍的E2E延迟。 我们将提出的算法与Max-SINR和Max-RSSI关联的性能进行比较。
【B.仿真结果】
图2显示了M = 40 AVs和N = 10 SBSs的V2I网络中可靠性的累积分布函数（CDF）。 图2中的结果表明，所提出的算法明显优于max-SINR和maxRSSI方案。 例如，在所提出的方案中，可靠性低于0.8的概率仅为30％，而max-SINR和max-RSSI的概率分别为95％和85％。 这种性能提升主要是由于执行AV到SBS关联和带宽分配时考虑了E2E延迟，而基准方案并未优化E2E延迟。
图3展示了E2E延时的CDF并比较了在一个V2I网络中三种不同方案的表现（在M=40,N=10下）。首先我们可以发现提出的方案可以以接近99％的高概率保证50 ms的端到端延迟。 但是，这两种基线方法都只能以小于90％的概率满足E2E延迟要求。 对于具有M = 40个AV的大型V2I网络，图3中的结果表明，所提出的算法可以有效地最小化E2E延迟。 显然，随着网络负载的减少，端到端延迟将减少。
为了显示传输和计算延迟对总体E2E延迟的影响，在M = 40 AV和N = 10 SBS的情况下，分别在图4和5中显示了这些度量的CDF。 将图4中的传输等待时间的值与图5中的计算等待时间进行比较，我们可以观察到边缘计算机的计算延迟是很长的（可以达到100 ms）并且不能忽略。 此外，图5显示，与基线算法相比，该方案考虑了计算延迟和每个边缘机的负载量，所以产生了更有效的AV到SBS关联。 这个特点可以看作是完成了负载平衡，我们的方法重点考虑每个SBS上分配任务的计算负载，而非AV的数量。
图6展示了每个AV的平均下行数据速率与AV数量的关系。显然，随着网络中AV的增多，AV的平均速率会降低。 结果如图6所示，提出的算法在数据速率方面明显优于基线方法。 例如，在M = 20 AV的V2I网络中，性能相比max-RSSI 和max-SINR方案，提升分别为49%和90%，
最后，图7显示了所提出算法的迭代次数（置信误差条为95％）相对于AV的数量的关系。 图7中的结果表明，即使对于具有10个SBS和30个AV的大型V2I网络，迭代次数也不会超过60。此外，结果表明迭代次数相对网络规模是多项式关系。
结论
在本文中，我们提出了一种用于自动驾驶汽车的超可靠，低延迟的车辆到基础设施通信的新颖框架。 我们已经表明，通过将AV间相互影响导致的计算延迟以及无线网络中的传输延迟联合考虑，所提出的框架可以最大化V2I网络的可靠性。 在这方面，我们基于劳动力匹配市场的概念提出了一种新颖的算法，该算法允许将AV与SBS进行分布式关联，同时考虑到每个SBS的有限计算和带宽资源。 此外，我们已经证明了该算法对AV到SBS的核心分配的收敛性。 仿真结果表明了该方案的各种优点。